Реферат: Структура аффинного пространства над телом

1. Введение

Чтобы лучше понимать аффинную структуру и не теряться от ее кажущейся сложности, можно обратиться к более общему понятию однородного пространства. Это даст также повод вспомнить, что понятие группы возникло путем абстракции из понятия группы преобразований, и, более того, оно полностью проявляет себя, когда мы рассматриваем действие группы на некотором множестве.

Считая хорошо известным понятие абстрактной группы, введем

Определение 1.1. Пусть - некоторая группа (с мультипликативным обозначением операции) и - ее нейтральный элемент.

Говорят, что действует слева на множестве , если определенно отображение , , такое, что набор отображений , удовлетворяет условиям

и . (1)

Аналогично говорят, что действует на справа, если определено отображение , , такое, что набор отображений , удовлетворяет условиям

и . (1/)

Соотношения (1) (соответственно (1/)) показывают, что ( соответственно )- это биекции на и что (соответственно ).

Например, любая группа действует сама на себе слева левыми сдвигами: и справа правыми сдвигами: .

Группа действует на себе слева также внутренними автоморфизмами: .

Условимся считать, если иное не оговорено, что действие группы на множестве понимается как действие слева.

Понятно, что для коммутативной группы оба действия совпадают; следует, однако, отметить, что одна и та же группа может действовать на множестве, в том числе и на себе, разными способами.

Определение 1.2. Пусть группа действует слева на множестве с законом действия . Говорят, что действует на транзитивно, если для любой пары элементов существует хотя бы один элемент , такой, что ; далее, говорят, что действие просто транзитивно, если этот элемент всегда единственный.

Пример. Линейная группа автоморфизмов действует транзитивно на , но это действие не является просто транзитивным, кроме случая .

Определение 1.3. Пусть группа действует слева на множестве . Стабилизатором подмножества множества называется множество .

Непосредственно ясно, что - подгруппа группы. Если множество состоит из одного элемента , то это подгруппа называется группой изотропии элемента .

Замечание. Стабилизатор является пересечением двух множеств и , которые не обязаны быть подгруппами . Например, если действует на себе трансляциями и - положительная полуось, то не является подгруппой, а .

Определение 1.4. Пусть - группа, действующая слева на ; орбитой элемента называется образ при отображении .

Если действует на транзитивно, то орбиты всех элементов совпадают с .

Замечание. На можно определить отношение эквивалентности, полагая , если существует элемент , такой, что ; классы эквивалентности являются орбитами элементов ; фактормножество по этому отношению назовем пространством орбит.

Однородные пространства

Определение 1.5. Однородным пространством, ассоциированным с группой , называется множество , на котором определено транзитивное действие группы .

Пример (типовой). Пространство смежных классов группы по ее подгруппе.

Пусть - группа, - ее подгруппа, - фактормножество, образованное левыми смежными классами относительно : элементы из объявляются эквивалентными, если существует элемент , такой, что ; класс эквивалентности элемента есть множество элементов вида , где .

Действие слева группы на определяется с помощью ; это действие, очевидно, транзитивно. Фактормножество является однородным пространством относительно этого действия.

Мы увидим, что всякое однородное пространство приводится (при помощи биекции) к пространству такого вида.

Теорема 1.1. Пусть - однородное пространство, ассоциированное с группой , и для любого пусть - группа изотропии . Тогда существует единственная биекция факторпространства на , такая, что для всех выполнено , где - каноническая проекция и - действие на .

Доказательство. Соотношение равносильно и, значит, или ; следовательно, отображение , переносится на фактормножество и представляется в виде , где - биекция.

Специальный случай

Если группа действует на просто транзитивно, то группы изотропии тривиальны; для каждой точки отображение , является биекцией, удовлетворяющей условию .

Эта биекция позволяет перенести на структуру группы , которая, однако, будет зависеть от выбора точки , т. е. образа нейтрального элемента. Говоря нестрого, допускает структуру группы, изоморфной , при произвольном выборе нейтрального элемента.

Так и будет обстоять дело в случае ”аффинной структуры”.

2.Аффинные пространства

Определение 2.1. Пусть - векторное пространство над произвольным телом . Аффинным пространством, ассоциированным с , называется множество ℰ, на котором определено просто транзитивное действие абелевой группы .

Это действие записывается обычно в виде

ℰℰ, .

Для любого биекция ℰ ℰ, называется трансляцией на вектор ; далее, для некоторой пары элементов ℰ единственный вектор , такой, что , обозначается .

Чтобы отличить элементы ℰ (называемые точками) от элементов (называемых векторами), мы будем преимущественно обозначать ”точки” прописными буквами латинского алфавита, такими, как , а ”векторы -строчными, например ; греческие буквы предназначаются для ”скаляров”.

Можно привести два равносильных данному определению 2.1. обычных определения, не опирающихся на понятие действия группы.

Определение 2.2. Аффинным пространством, ассоциированным с , называется множество ℰ, снабженное семейством биекций , таких, что

a) ℰ и ;

b) для любой пары ℰℰ существует единственный вектор , такой, что .

Определение 2.3. Аффинным пространством, ассоциированным с , называется множество ℰ, снабженное отображением ℰℰ, обозначаемым , таким, что

a) для каждого ℰ отображение ℰ, биективно;

b) для любых точек из ℰ выполнено соотношение Шаля

Заметим, что из этих условий следует, что для любой точки ℰ мы имеем .

От определения 2.3. к определению 2.2. можно перейти, обозначив через единственную точку , такую, что , и заметив, что соотношение Шаля равносильно . Переход от определения 2.2. к определению 2.1. непосредственно ясен.

Из какого бы определения мы ни исходили, существенным остается тот факт, что для любой точки ℰ отображение ℰ, есть биекция; эта биекция позволяет перенести на ℰ векторную структуру .

Обозначения. Полученная таким путем векторная структура на ℰ будет называться векторной структурой с началом ; множество ℰ с этой структурой будет обозначаться ℰA.

Говоря нестрого, аффинное пространство выглядит как векторное пространство, начальный (нейтральный) элемент которого еще не выбран. Аффинные свойства ℰ- это те свойства векторного пространства ℰA, которые не зависят от выбора точки .

Таким образом, можно было бы, пренебрегая аффинной структурой, свести все задачи аффинной геометрии к задачам векторного характера путем выбора начальной точки; так и делается в математическом обиходе. Но больше в духе ”внутреннего” исследования была бы работа без выбора начальной точки, позволяя яснее представить именно аффинные свойства ℰ. Так мы и поступим, не забывая при этом, что введение векторной структуры с надлежащим выбором начальной точки часто проясняет дело.

Размерность аффинного пространства

Пусть ℰ- аффинное пространство, ассоциированное с векторным пространством . По определению, размерность ℰ равна размерности .

В частности, любое одноточечное множество допускает единственную аффинную структуру размерности , ассоциированную с нулевым векторным пространством.

Аффинные подпространства

(Линейные аффинные многообразия)

Пусть ℰ- аффинное пространство, ассоциированное с векторным пространством . Каждое векторное подпространство пространства образует подгруппу группы , действующую на ℰ трансляциями. По определению, орбиты действия на ℰ называются линейными аффинными многообразиями (сокращенно ЛАМ) с направлением . Группа , действующая просто транзитивно на каждой из этих орбит определяет тем самым на каждой из них аффинную структуру, ассоциированную с ; поэтому мы называем эти орбиты (ЛАМ) также аффинными подпространствами в ℰ.

Если есть ЛАМ с направляющим подпространством и - точка , то допускает структуру векторного пространства с началом и есть векторное подпространство в ℰA. Обратно, любое ВПП пространства ℰA есть ЛАМ, проходящее через ; сформулируем

Предложение 3.1. Аффинные подпространства в ℰ, проходящие через точку , суть векторные подпространства векторного пространства ℰA.

Это краткое рассмотрение показывает, что направление ЛАМ пространства ℰ полностью определяется заданием множества точек .

Другие определения.

Предложение 3.1. показывает, что данное выше определение эквивалентно следующему элементарному определению:

Определение 3.1. Непустое подмножество аффинного пространства ℰ называется линейным аффинным многообразием, если в существует точка , такая, что является векторным подпространством в .

Приняв определение 3.1., можно непосредственно установить следующее

Предложение 3.2. Пусть - непустое подмножество в ℰ и - точка , такая, что есть векторное подпространство в . Тогда для любой точки из множество совпадает с .

Доказательство. есть множество векторов , где ; таким образом, есть образ при биекции , , и поскольку , то .

Установив это, легко убедиться, что наделено структурой аффинного пространства, ассоциированного с векторным пространством , которое не зависит от точки .

Вместо того, чтобы исходить из векторной структуры , можно использовать отношение эквивалентности, связанное с действием на : ЛАМ суть классы эквивалентности для этого отношения, и мы приходим к следующему равносильному определению:

Определение 3.2. Пусть - векторное подпространство в и - отношение эквивалентности, определяемое на ℰ с помощью

;

аффинными многообразиями с направлением называются классы эквивалентности по отношению .

Существуют и другие способы определить ЛАМ пространства ℰ, но нам кажется, что данные выше определения ведут к наиболее простому способу изложения дальнейшего.

Случай векторного пространства.

Каждое векторное пространство канонически снабжено аффинной структурой, так как действует на себе трансляциями; в этом случае нулевой вектор называется также ”началом” и

ЛАМ пространства , проходящие через , суть векторные подпространства в ; ЛАМ, проходящие через точку , суть образы векторных подпространств при параллельном переносе .

Ради кратности ЛАМ, не проходящие через начало, будут называться собственно аффинными (поскольку они не являются ВПП в ).

Размерность линейного аффинного многообразия

Вернемся к случаю произвольного аффинного пространства ℰ; предшествующие рассмотрения позволяют определить размерность ЛАМ как размерность его направляющего ВПП. Отсюда появляются понятия: аффинной прямой (ЛАМ размерности 1) и аффинной плоскости (ЛАМ размерности 2). ЛАМ размерности суть точки ℰ.

Аффинной гиперплоскостью называется ЛАМ, направляющее подпространство которого есть векторная гиперплоскость.

Пересечение линейных аффинных многообразий

Предложение 3. 3. Пусть - семейство аффинных подпространств в ℰ и для каждого - направляющее подпространство для .

Если пересечение непусто, то оно является аффинным подпространством в с направляющим .

Доказательство сразу получается из определения 3.1. При тех же обозначениях имеет место

Предложение 3.4. Для того, чтобы пересечение двух ЛАМ в ℰ было непустым, необходимо и достаточно, чтобы существовали такие точки и , что , и тогда

Доказательство. Если , то для любых , имеем и . Таким образом, .

Обратно, если существуют и , такие, что , то можно представить в виде , где , . Тогда точка , определяемая условием , принадлежит и, как легко видеть, . Это доказывает, что принадлежит также , а тем самым не пусто.

Из предложения 3.4. можно получить примеры ЛАМ с пустым пересечением, а также

Предложение 3.5. Если , - аффинные подпространства в ℰ, направляющие которых взаимно дополняют друг друга в , то и имеют единственную общую точку.

Параллелизм

Определение 3.3. Говорят, что два линейных аффинных многообразий , вполне параллельны, если они имеют одно и то же направляющее подпространство: .

Более общо, говорят, что параллельно , если направляющие пространства , многообразий , удовлетворяют включению .

Можно проверить, что отношение ” вполне параллельно (соответственно параллельно) ” равносильно существованию трансляции пространства ℰ, такой, что (соответственно ).

Аффинное подпространство, порожденное подмножеством пространства ℰ

Предположение 3.6. Если - непустое подмножество в ℰ, то существует единственное аффинное подпространство в ℰ, обозначаемое , содержащее и обладающее следующим свойством:

Любое аффинное подпространство ℰ, содержащее , содержит и .

Говорят, что порождено .

Коротким способом доказательства предложения 3.6. является применение предложения 3.3.: есть пересечение всех ЛАМ, содержащих . Недостаток этого рассуждения в том, что приходится привлекать семейство ”всех ЛАМ, содержащих ”, о котором мало что известно и которое обычно даже несчетно!

Более элементарный и конструктивный способ состоит в выборе в начальной точки , что сводит задачу к отысканию наименьшего векторного подпространства в ℰA, содержащего (поскольку ЛАМ, содержащее , являются ВПП в ℰ). Таким образом, есть ВПП в ℰA, порожденное ; при этом сам характер задачи показывает, что это ВПП не зависит от выбора точки в . Если мы заметим, что направляющее подпространство для есть ВПП в , порожденное векторами , то получим также

Предложение 3.7. Пусть - непустое подмножество в ℰ; для каждой точки положим . Тогда векторное пространство не зависит от выбора и есть ЛАМ, проходящее через с направлением .

Можно дать прямое доказательство этого утверждения, аналогичное доказательству предложения 3.2.

В частности, если - конечное множество, то векторное пространство не зависит от и, следовательно, совпадает с

и .

Отсюда вытекает

Предложение 3.8. Размерность аффинного подпространства, порожденного точками пространства ℰ не превосходит ; его размерность равна тогда и только тогда, когда векторов () образуют свободное семейство.

Другие свойства ЛАМ изучаются в связи с понятием барицентра.

Барицентры: приложения к изучению аффинных подпространств

В последующем ℰ всегда обозначает аффинное пространство, ассоциированное с левым векторным пространством над, вообще говоря, некоммутативным телом . ”Взвешенной точкой” называется элемент ℰ.

Теорема 4.1. Для каждого конечного семейства (системы) взвешенных точек, такого, что , существует единственная точка , удовлетворяющая любому (а тогда и двум остальным) из следующих трех условий a), b), c):

a) ,

b) ℰ ,

c) ℰ .

Эта точка называется барицентром (центром тяжести) системы . Мы обозначим ее .

Эквивалентность трех условий легко устанавливается с помощью соотношения Шаля.

Свойства. a) Однородность (слева).

Предложение 4.2. Для любого имеем

b) Ассоциативность.

Предложение 4.3. Пусть - разбиение , т.е. совокупность непустых попарно непересекающихся подмножеств , таких, что .

Если для любого скаляр отличен от нуля и мы положим , то

Доказательства получаются непосредственно

Замечания. По определению 4.2. можно всегда привести дело к случаю, когда ”полная масса” системы , т.е. равна 1. В этом и только в этом случае можно положить

Для успешного использования этого обозначения следует заметить, что соотношение равносильно каждому из следующих утверждений:

и ℰ , (1)

ℰ , (2)

так как (2) влечет за собой (1).

Эквибарицентром конечного подмножества пространства ℰ называется точка . Она существует только тогда, когда характеристика не является делителем числа .

Следующее утверждение показывает, что отыскание барицентра сводится, за некоторыми исключениями, к последовательному построению барицентров пар точек.

Предложение 4.4. Пусть - конечное семейство взвешенных точек, таких, что для всех , и .

Если характеристика отлична от 2, то существует разбиение множества , такое, что

и .

Доказательство. Если одна из сумм отлична от нуля, то достаточно положить и .

Если все суммы равны нулю, то все равны одному и тому же элементу , такому, что , где .

Если характеристика отлична от 2, то , и, поскольку не равно нулю, получим искомое разбиение, выбирая как двухэлементное подмножество, а как подмножество из элементов.

Следствие. Если характеристика не равна 2, то построение барицентра точек приводится к последовательному построению барицентров пар.

Приложения к линейным аффинным многообразиям

Теорема 4.5. Если - непустое подмножество в ℰ, то есть множество барицентров конечных семейств взвешенных точек с носителями в .

Доказательство. Уточним сначала, что под носителем семейства понимается множество .

Условившись об этом, выберем некоторую точку в . Барицентры семейства с носителями в суть точки , удовлетворяющие соотношению вида

, (3)

где и . При этом соотношение (3) влечет за собой и поэтому (см. предложение 3.7). Обратно, если - точка из , то найдутся точки , принадлежащие , и скаляры ( с суммой, необязательно равной 1), такие, что ; это соотношение также записывается в виде

с и ;

таким образом, есть барицентр системы с носителем в .

Определение 4.1. Подмножество ℰ называется аффинно порождающим ℰ, если ℰ; оно называется аффинно свободным, если любая любая точка из единственным образом представляется в виде

, где и при любом .

Множество, одновременно аффинно свободное и аффинно порождающее, называется аффинным репером.

Выбирая начало в и пологая , легко видеть, что аффинно свободное (соответственно аффинно порождающее) тогда и только тогда, когда свободное (соответственно множество образующих). (Напомним, что не зависит от выбора .) Отсюда вытекает

Предложение 4.6. Для того, чтобы подмножество пространства ℰ было аффинно порождающим, необходимо и достаточно, чтобы не содержалось ни в какой аффинной гиперплоскости в ℰ.

Наконец, применяя предложение 3.7, получим

Предложение 4.7. Если ℰ- аффинное пространство конечной размерности , то любой его аффинный репер образован точками.

Обратно, для того, чтобы точек в ℰ образовали аффинный репер, необходимо и достаточно, чтобы векторов образовали базис , или (эквивалентное условие) чтобы точки не принадлежали одной аффинной гиперплоскости.

Заметим, что если есть ЛАМ конечной размерности в ℰ и - аффинный репер в , то есть множество точек с . Этот способ параметризации часто полезен. В частности, аффинная прямая, соединяющая две точки в ℰ, есть множество точек .

Характеризация аффинных подпространств

Следующая теорема оправдывает элементарное определение плоскости в школьном курсе геометрии как такого множества точек, что каждая прямая, имеющая с ним две общие точки, вся принадлежит .

Теорема 4.8. для того, чтобы непустая часть пространства была линейным аффинным многообразием, необходимо и достаточно, чтобы

a) если - любая прямая, соединяющая две точки , содержалась в ;

b) если - эвибарицентр любых трех точек лежал в .

Доказательство. Нам уже известна необходимость этого условия. Для доказательства достаточности выберем в точку и покажем, что есть ВПП пространства .

a) Предположив, что , установим прежде всего, что условия и влекут .

Действительно, по предположению существует точка , такая, что . Точка , определенная условием , принадлежит прямой (АВ) и, значит, , откуда следует, что .

Рассмотрим далее два любых вектора и в и выберем (что возможно, так как не сводится к ). Точки и (см. рис. 1) принадлежат соответственно прямым (АВ) и (АС), а поэтому и . Следовательно, точка принадлежит , откуда . Итак есть ВПП в .

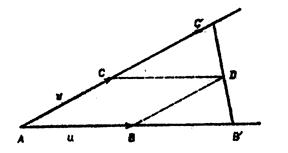
Рис. 1

b) Если , то тривиальным образом влечет (так как может принимать только два значения 0, 1). Если , - два вектора из , то точка , определяемая условием , есть эквибарицентр , откуда и вытекает наше утверждение.

Аффинные и полуаффинные отображения

Определение 5.1. Пусть ℰ, - два аффинных пространства, ассоциированных соответственно с векторными пространствами , .

Отображениеℰназывается полуаффинным (соответственно аффинным), если в ℰ существует такая точка , что отображение , полулинейно (соответственно линейно).

Предложение 5.1. Если в ℰ существует точка , удовлетворяющая вышеуказанным требованиям, то им удовлетворяет любая точка ℰ и отображение не зависит от .

Доказательство. Для любой пары ℰ имеем в силу линейности

что и доказывает требуемое.

Обозначения. Отображение обозначается и называется полулинейной (соответственно линейной) частью .

Истолкование. Фиксируем в ℰ некоторую точку и снабдим , векторными структурами, принимая за начало в ℰ точку , а в - точку . Тогда будет полуаффинным (соответственно аффинным) в том и только том случае, если - полулинейное (соответственно линейное) отображение ℰА в .

В частности, изучение полуаффинных (соответственно аффинных) отображений пространства ℰ в себя, допускающих неподвижную точку , сводится к изучению полулинейных (соответственно линейных) отображений ℰА в себя.

Так обстоит дело в случае геометрий, проектирований и симметрий (см. ниже).

Важно заметить, что полуаффинные (соответственно аффинные) отображения полностью определяется своей полулинейной (соответственно линейной) частью и образом одной точки.

Если , - два векторных пространства, то полуаффинное (соответственно аффинное) отображение и есть отображение вида , где полулинейно (соответственно линейно), а - постоянный элемент.

Непосредственные следствия. Если ℰ полуаффинно, то

1) Образ ЛАМ в ℰ есть ЛАМ в .

2) Прообраз ЛАМ в есть ЛАМ в ℰ или пустое множество.

3) Для любой системы взвешенных точек ℰ образ барицентра есть барицентр , где обозначает изоморфизм тел, ассоциированных с .

Применение аффинных реперов

Теорема 5.2. Пусть ℰ, - аффинные пространства над телами ,, - изоморфизм на , - аффинный репер в ℰ и - семейство точек , индексированное тем же множеством индексов .

Тогда существует единственное полуаффинное отображение пространства ℰ в , ассоциированное с изоморфизмом , такое, что для всех .

Более того, биективно (соответственно инъективно, сюръективно) тогда и только тогда, когда семейство есть аффинный репер (соответственно свободное семейство, семейство образующих) для .

Доказательство. Вернемся к теореме , взяв одну из точек в качестве начала в ℰ, а соответствующую точку - в ; отображение определяется равенством

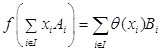
для любого конечного подмножества и любой системы скаляров , таких, что, .

В частности, аффинное отображение ℰ в определяется заданием образа аффинного репера из ℰ.

Приложение: уравнение аффинной гиперплоскости или ЛАМ

Опираясь на исследование, проведенное в параграфе II.6, легко получаем

Предложение 5.3. Пусть ℰ- аффинное пространство над телом . Тогда

a) Если ℰ - непостоянное аффинное отображение, то - аффинная гиперплоскость в ℰ с направлением .

b) Обратно, если - аффинная гиперплоскость в ℰ, то существует аффинное отображение ℰ, такое, что , и все аффинные отображения ℰ в с этим свойством суть отображения , где .

Если ℰ- аффинное пространство конечной размерности , то каждое ЛАМ размерности в ℰ определяется системой уравнений вида , где - аффинные отображения ℰ в , линейные части которых независимы.

Характеризация аффинных отображений

Теорема 5.4. Пусть ℰ- два аффинных пространства над одним и тем же телом . Для того, чтобы отображение ℰ было аффинным, необходимо и достаточно, чтобы

a) при

ℰℰ

;

b) при образ эквибарицентра любых трех точек ℰ был эквибарицентром их образов.

Доказательство (аналогичное случаю теоремы 4.8.).

a) При фиксированной точке ℰ соотношение a) показывает, что для любого вектора направляющего пространства имеем

Отображение удовлетворяет, следовательно, условию .

Чтобы доказать, что выполняется и условие для любых , выберем такие , что , и , определим точки , условиями , . Применяя условие a), получим тогда ,

откуда

Можно также сформулировать теорему 5.4. так: отображение ℰ в является аффинным тогда и только тогда, когда его ограничение на любую аффинную прямую в ℰ аффинно.

В дальнейшем мы дадим чисто геометрическую характеристику полуаффинных отображений.

Неподвижные точки аффинных и полуаффинных отображений.

Теорема 5.5. Если - полуаффинное отображение и множество его неподвижных точек не пусто, то оно является ЛАМ с направляющим множеством , состоящим из неподвижных элементов отображения .

С другой стороны, если конечномерно и не имеет других неподвижных элементов, кроме 0, то имеет единственную неподвижную точку.

Доказательство. Если фиксировать точку , условие равносильно и, значит, условию где

· Если - неподвижная точка то равносильно откуда вытекает первое утверждение.

· Если , то отображение инъективно и потому в случае конечной размерности биективно; в существует единственная точка такая, что откуда следует второе утверждение.

Важное замечание. Если - произвольное отображение и - биекция, то

Это общее замечание особенно полезно в случае аффинных отображений.

Аффинные и полуаффинные группы.

Если и - два аффинных (соотв. полуаффинных) отображения, то также есть аффинное (соотв. полуаффинное) отображение и Отсюда выводится

Теорема 5.6. Пусть - аффинное пространство, ассоциированное с векторным пространством Аффинные (соотв. полуаффинные) биекции на образуют группу, которую мы обозначаем (соотв. ). Отображение (линейная или полулинейная часть) есть гомоморфизм на и на группу полулинейных биекций на .

Наконец, для любой точки в ограничение на группу изотропии точки в (соотв. ) является изоморфизмом этой группы на (соотв. ).

Последнее утверждение получим, выбирая в качестве начала в .

Следствие. Если подгруппа в (соотв. в ), то есть подгруппа в (соотв. в ); при этом если инвариантная подгруппа, то такова же и .

В частности, если то есть инвариантная подгруппа в , образованная трансляциями.

Если то есть инвариантная подгруппа в , образованная трансляциям и центральными симметриями.

Если инвариантная подгруппа группы , образованная векторными гомотетиями, то есть инвариантная подгруппа в , называемая группой дилатаций.

Пусть дилатация, не сводящаяся к трансляции; тогда векторная гомотетия вида где В этом случае имеет единственную неподвижную точку определяемую из условия где произвольная точка . Таким образом, выражается как Такое отображение называется гомотетией с центром и коэффициентом

Сформулируем

Предложение 5.7. Трансляции и гомотетии составляют инвариантную подгруппу группы , называемую группой дилатаций . Мы обозначаем ее .

Если основное тело коммутативно, то группа является инвариантной подгруппой группы .

Проектирования

Назовем проектированием любое аффинное отображение пространства в себя, удовлетворяющее условию

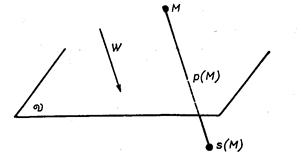
Рис. 2

Для такого отображения любая точка является неподвижной; принимая такую точку за начало, мы приходим к случаю проектирования для векторного пространства . Отсюда вытекает существование таких отображений, а также следующая их геометрическая характеризация:

Предложение 5.8. Отображение является проектированием, если существует ВПП пространства и ЛАМ в с направляющим подпространством дополнительным к , такие, что для любой точки ее образ есть точка пересечения с ЛАМ, проходящим через с направлением (рис. 2).

Аффинные симметрии

Теорема 5.9. Пусть 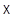- аффинное пространство, ассоциированное с векторным пространством 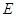над телом 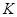характеристики .

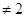Для того, чтобы аффинное отображение было инволютивным, необходимо и достаточно, чтобы оно имело по меньшей мере одну неподвижную точку и чтобы его линейная часть была векторной симметрией

Такое отображение называется аффинной симметрией.

Доказательство. Если и , то образом середины отрезка будет середина отрезка таким образом, эта точка инвариантна при отображении и, выбрав ее за начало, мы сведем дело к векторному случаю.

Предложение 5.10. Отображение является аффинной симметрией, если существуют ВПП пространства и ЛАМ с направлением, дополнительным к такие, что для любой точки (см.рис.2)

1).

2). Середина принадлежит .

Если сводится к одной точке то и есть центральная симметрия с центром

Теорема Фалеса

Пусть по-прежнему есть ВПП в и - два аффинных пространства в , направляющие которых соответственно дополнительны к Обозначим через (соотв. ) ограничение проектирования на (соотв.) параллельно Тогда, как легко видеть, является аффинной биекцией на , обратная к которой есть . Образ точки определяется условиями и (см. рис. 3).

В более общей форме теорема Фалеса есть не что иное, как констатация того факта, что установленное

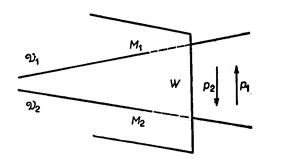
Рис.3

указанным способом соответствие между и является аффинным.

В частности, если векторная гиперплоскость, то справедлива

Теорема 5.11. Аффинные гиперплоскости, параллельные некоторой фиксированной гиперплоскости, высекают на произвольной паре не параллельных им прямых пропорциональные отрезки.

§6. Каноническое погружение аффинного пространства в векторное. Приложения.

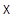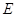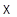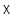Пусть снова - аффинное пространство, ассоциированное с векторным пространством . Как мы уже видели, выбор начала в позволяет отождествить с 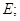теперь мы докажем, что 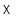канонически отождествляется с аффинной гиперплоскостью некоторого пространства 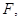изоморфного

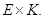
Метод будет состоять в сопоставлении каждой точке отображения

Предварительно сформулируем такое утверждение:

Лемма. Пусть левое векторное пространство над телом а произвольное множество. Тогда множество отображений в есть левое векторное пространство над по отношению к обычным операциям сложения функций и умножению их слева на скаляры:

В силу доказанного искомое векторное пространство будет ВПП в , порожденным отображениями Поэтому мы начнем с изучения этого пространства

Предложение 6.1. Пусть - векторное подпространство в , порожденное функциями пуст, далее, элемент из . Тогда

А). Сумма зависит только от функции и притом линейно, т.е. является линейным отображением в которое мы обозначим

Б). Если то существует единственная точка , такая, что .

В). Если то постоянна.

Доказательство. Заметим сначала, что утверждение А) не очевидно, так как могут существовать различные системы взвешенных точек , такие, что но оно легко вытекает из того факта, что для любой пары выполнено соотношение

, (1)

которое доказывает существование и линейность функции

Б). Если выберем в произвольную точку Соотношение (1) показывает, что в существует единственная точка такая, что она определяется условием Из (1) также видно, что эта точка – единственная, для которой Таким образом, барицентр семейства зависит только от функции

В). Наконец, последнее утверждение также вытекает из (1).

Следствие. является теоретико-множественным объединением векторного пространства постоянных функций и множества функций вида

Предложение 6.2. Пусть отображение и пусть отображение в которое любому вектору ставит в соответствие постоянную функцию, равную на .

Тогда аффинно с линейной частью и потому инъективно; при этом есть аффинная гиперплоскость в с уравнением

Доказательство. Для любой пары разность есть постоянная функция ; положим . Таким образом, аффинно, и инъективно, как и

С другой стороны, как показывает предыдущее предложение, функции суть элементы удовлетворяющие условию .

Теорема 6.3. К каждому аффинному пространству , ассоциированному с векторным -пространством , можно канонически присоединить:

· Векторное пространство изоморфное ,

· Ненулевую линейную форму на ,

· Аффинную инъекцию , такую, что - аффинная гиперплоскость в с уравнением

Доказательство. Остается только установить изоморфизм между и . Для этого достаточно заметить, что какова бы ни была точка, отображение , линейно и биективно. Установленный таким путем изоморфизм очевидным образом зависит от выбора точки .

Заметим, что аффинная гиперплоскость имеет в качестве направляющей векторную гиперплоскость постоянных функций, которая отождествляется с .

Замечания. 1). Векторную структуру на множестве можно определить непосредственно, не прибегая к векторному пространству , но это связано с утомительными выкладками.

2). Особый интерес теоремы 6.3 в том, что она обеспечивает каноническое погружение единственным образом определяемое заданием.

Обозначения. Векторное пространство , построенное таким образом, называется векторным продолжением и обозначается .

Если имеет размерность то размерность равна . Мы увидим, что введение этого пространства позволяет прояснить многие вопросы.

§7. Приложения теоремы о погружении.

Векторная интерпретация барицентров.

Вернемся к обозначениям §6. Инъекция позволяет нам отождествить с аффинной гиперплоскостью в , в то время как ее линейная часть позволяет отождествить с векторной гиперплоскостью

Предложение 7.1. Пусть конченое семейство взвешенных точек , где точки отождествлены с элементами . Для того, чтобы элемент из принадлежал (соотв. ), необходимо и достаточно, чтобы (соотв. ).

Доказательство. Это вытекает из соотношения

Правило. Отождествление с подмножеством в позволяет без предосторожностей записывать любые конечные линейные комбинации элементов . Но такая комбинация представляет элемент из только тогда, когда ( этот элемент будет барицентром системы ); если же то представляет элемент из равный для любой точки .

Приложения. 1). Для того, чтобы три точки из были коллинеарны, необходимо и достаточно, чтобы существовали не равные одновременно нулю скаляры такие, что

и (1)

Соотношения (1) на самом деле равносильны одному соотношению ; они интересны своей симметричной формой относительно и возможностью складывать подобные соотношения.

2). Если то барицентром системы является точка пересечения с векторной прямой с направляющей в .

3). Для того чтобы семейство точек из было аффинно свободным (соотв. аффинно порождающим), необходимо и достаточно, чтобы семейство было свободным (соотв. семейством образующих) в векторном пространстве

В частности, аффинный репер является базисом содержащимся в

Векторная интерпретация аффинных отображений.

Мы начнем с установления одного общего результата, независимого от теории векторных продолжений

Предложение 7.2. Пусть , - два векторных пространства над одним и тем же телом и (соответственно ) – аффинная гиперплоскость в (соотв. ), не проходящая через начало; обозначим (соответственно ) векторную гиперплоскость, параллельную (соответственно ).

А) Если - линейное отображение, такое, что , то ограничение на есть аффинное отображение в , линейная часть которого есть ограничение на .

Б) обратно, если - аффинное отображение, то существует единственное линейное отображение , ограничения которого на совпадает с .

Доказательство.

А) Если линейно и , то для любых точек из имеем и . Ограничения на аффинно с линейной частью , .

Б) Обратно, пусть- аффинное отображение. Фиксируем точку в и обозначим через (соответственно ) векторную прямую в (соответственно ), порожденную (соответственно ) (рис 4). Тогда , , и искомое линейное отображение должно удовлетворять следующим двум условиям:

1. ,

2. Ограничения на равно линейной части .

Но существует единственное линейное отображение из в , удовлетворяющее этим условиям ( определено своими ограничениями на дополнительные ВПП и пространства ); тогда ограничение на - есть аффинное отображение с той же линейной частью, что и , и принимающее в то же значение, что и , а тем самым равное , откуда вытекает доказываемый результат.

Существует, следовательно, биективное соответствие между аффинными отображениями в и линейными отображениями в , удовлетворяющими условию .

С другой стороны, если , и , это соответствие сохраняет композицию отображений (композиция ограничений двух отображений совпадает с ограничением их композиции).

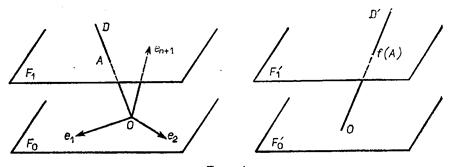
Рис.4

Наконец, если - автоморфизм и - аффинная гиперплоскость в , то включение влечет равенства . В самом деле, есть аффинная гиперплоскость в , и достаточно применить следствие теоремы II 6.2, вернувшись к векторному случаю путем замены начала в .

Т.о. мы можем сформулировать

Предложение 7.3. Пусть - векторное пространство, - аффинная гиперплоскость в , не проходящая через начало. Существует изоморфизм группы аффинных биекций на стабилизаторе в (подгруппу , состоящую из изоморфизмов , для которых ).

Эти результаты применимы, в частности, к случаю, когда, , - векторные продолжения аффинных пространств , , а , - образы , при канонических погружениях , : всякое аффинное отображение в , отождествляется с линейным отображением пространства в пространство , удовлетворяющим требованию , и группа аффинных биекций отождествляется с подгруппой , сохраняющей аффинную гиперплосклость

Случай конечной размерности.

Если аффинное пространство имеет конечную размерность , то в можно выбрать базис так, что при и . Тогда есть декартов репер в с началом (рис 4).

В этом случае является множеством точек пространства , таких, что ; следовательно, это аффинная гиперплоскость с уравнением в базисе . Эндоморфизмы пространства , удовлетворяющие условию , - это те эндоморфизмы, матрица которых в базисе имеет вид

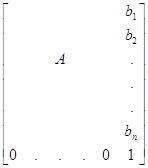, (2)

где - квадратная матрица порядка . Эндоморфизму с матрицей (2) соответствует аффинное отображение , координатное выражение которого в декартовом репере имеет форму

, (3)

Матричные вычисления показали бы, что для этого соответствия соблюдаются правила композиции отображений. С другой стороны, эндоморфизм с матрицей (2) обратим тогда и только тогда, когда обратима матрица (2), и тогда выполняется и равенство . Таким образом, получается

Теорема 7.4. Группа аффинных биекций -мерного аффинного пространства изоморфна подгруппе линейной группы , образованной матрицами вида (2), где принадлежит .

В частности, группа аффинных биекций тела изоморфна подгруппе в , состоящей из матриц вида .

8.Геометрическая характеризация инъективных полуаффинных отображений.

Ниже мы обозначаем через , два аффинных пространства, ассоциированных соответственно с векторными пространствами над произвольными телами . Мы дадим чисто геометрическую характеризацию полуаффинных отображений в . Для ясности начнем со случая инъективных отображений.

Теорема 8.1. Допустим, что . Для того, чтобы инъективное отображение было полуаффинным, необходимо и достаточно, чтобы оно удовлетворяло следующим двум условиям:

1. Образ любой аффинной прямой из был аффинной прямой в ;

2. Образы двух параллельных прямых был параллельными прямыми.

Доказательство. Необходимость условия очевидна. Доказательство

достаточности проведем в несколько этапов, все время предполагая, что удовлетворяет условиям 1) и 2).

А). Образы при двух различных прямых , из суть также две различные прямые.

В самом деле, пусть , - прямые в , имеющие один и тот же образ , пусть - две различные точки их общего образа. Тогда прообразы точек и принадлежат и одновременно и различны (в силу иньективности ), откуда следует, что .

Б). Отображение , не зависит от выбора в .

В самом деле, пусть другая точка и , таковы, что . Если

- несплющенный параллелограмм, то из 2) и А) следует, что его образ тоже настоящий параллелограмм, откуда

Если точки принадлежат одной прямой , то предположение позволяет выбрать в точки так, что . Применяя предыдущий случай, имеем

откуда.

Отображение обозначаем отныне просто .

В). Отображение инъективно и удовлетворяет условию

. (1)

Инъективность сразу следует из инъективности . С другой стороны, для любых данных выберем в такие точки , , , и . Тогда .

Д). Существует отображение , такое, что

. (2)

Доказательство. Достаточно найти , удовлетворяющее условию (2) при . Для заданной пары выберем , , в так, что , . Так как точки , и коллинеарны, то коллинеарны и векторы ; отсюда вытекает существование некоторого скаляра, скажем , такого, что . Остается доказать, что не зависит от вектора (по предположению ненулевого).

1). Если два неколлинеарных вектора, то неколлинеарны и , ; в противном случае образы двух прямых , , проходящих через одну и ту же точку с направляющими , совпадали бы, что невозможно в силу А).

Для любого имеем

откуда в силу неколлинеарности ,

2). Если , - коллинеарные ненулевые векторы, то предположение позволяет выбрать так, что пары и свободны. Отсюда находим, что

Так для каждого отображение , есть константа, мы обозначим ее через .

Е). Отображение является изоморфизмом тел.

Выбрав , мы увидим прежде всего, что соотношения и влекут (с учетом )

и ,

т.е. показывают, что - гомоморфизм тел.

Наконец, для любой точки отображение есть биекция на прямую ; ограничение на есть биекция на прямую . Следовательно, композиция , биективна. Отсюда вытекает, что отображение биективно.

Итак, изоморфизм тел, полулинейное отображение, ассоциированное с , и полуаффинное отображение.

Случай плоскости.

Если и двумерны, то условие 2) в теореме 8.1 следует из условия 1) и инъективности . Мы можем, таким образом, сформулировать

Следствие. Если ,аффинные плоскости и - инъективное отображение, такое, что образ любой прямой в есть прямая в , то полуаффинное отображение.

Замечание. Условия теоремы 8.1 выполняются, в частности, если инъективное отображение в себя, такое, что образ любой прямой есть прямая, параллельная ; тогда можно непосредственно доказать, что дилатация.

9.Основная теорема аффинной геометрии.

Исходя из теоремы 8.1 и опираясь на характеризацию аффинных многообразий, представленную теоремой 4.8, мы докажем здесь следующую теорему:

Теорема 9.1. Пусть ,аффинные пространства над телами , , отличными от поля ; для того, чтобы отображение было полуаффинным, достаточно, чтобы

1). Образ любой прямой в был прямой в , либо сводился к одной точке.

2). Аффинное подпространство в , порожденное , имело размерность .

Мы подразделим доказательство этой теоремы на семь лемм; в каждой из них предполагается, что удовлетворяет условиям 1) и 2).

Лемма 1. Если есть ЛАМ в , то - ЛАМ в .

Доказательство. Пусть и - две различные точки в . Тогда прямая есть по условию 1) образ прямой ; так как прямая содержится в , прямая содержится в . Результат теперь вытекает из теоремы 4.8.

Лемма 2. Если - ЛАМ в и множество непусто, то оно является ЛАМ в .

Доказательство. Результат очевиден, если сводится к одной точке. В противном случае для любой пары различных точек , прямая содержится в согласно 1). Таким образом, прямая содержится в и теорема 4.8 показывает, что есть ЛАМ.

Лемма 3. Для любой непустой части пространства

. (1)

Доказательство. есть ЛАМ в , содержащее ; по лемме 1, есть ЛАМ в , содержащее . Отсюда следует включение

Аналогично, по лемме 2, есть ЛАМ в , содержащее , а потому и ; имеет место включение ; применение отображения дает .

Окончательно получаем равенство (1).

Лемма 4. Пусть - пара параллельных прямых в . Если сводится к точке, то же имеет место и для . Если - прямая, то и - прямая, параллельная .

Доказательство. Мы можем предположить, что . Тогда есть ЛАМ размерности 2 в , порожденное двумя точками , одной из прямых и точкой другой прямой; по леммам 2и 3, есть ЛАМ размерности .

А). Покажем сначала, что либо .

Допустим, что и действительно имеют общую точку. Тогда найдутся точки и , такие, что . Выбирая и полагая по-прежнему , получим с помощью леммы 3, что

и аналогично

откуда .

Поскольку сформулированное утверждение при очевидно, будем далее полагать , т.е. считать, что и не имеют общих точек.

Б). Предположим, что - прямая в и ; тогда имеет размерность 2.

Если бы на прямой существовали две точки , такие, что , то для любой точки мы имели бы и , и тогда не было бы двумерным вопреки предположению. Отсюда следует, что - прямая.

Значит, и - две прямые без общих точек, лежащие в одном ЛАМ размерности 2, т.е. параллельные.

В). Если сводится к одной точке, то меняя ролями ии применяя результат Б), мы видим, что также сводится к точке.

Лемма 5. Если пара точек в , таких, что множества ,

непусты, то и - ЛАМ с общим направлением.

Доказательство. По лемме 2, и суть ЛАМ в . Предполагая, что , фиксируем точку в и точку в ; параллельный перенос на вектор обозначим через . Для любой точки прямая параллельна прямой, и поскольку образ прямой сводится к одной точке , то образ прямой сводится к одной точке . Таким образом, влечет и имеет место включение .

Меняя ролями и , получим включение , откуда . Итак, , имеют общее направление.

Лемма 6. Обозначим через общее направление непустых ЛАМ в вида , где , и пусть - факторпространство по отношению эквивалентности , определенному условием .

Тогда имеет единственную аффинную структуру, такую, что каноническая проекция является аффинной.

Доказательство. Выбор начала в сводит дело к случаю факторпространства векторного пространства По его векторному подпространству , и оказывается, что достаточно применить теорему II.4.3, приняв точку за начало в .

Отметим, что является пространством орбит действия группы трансляций на ; это есть множество ЛАМ с направлением .(см. §2).

Лемма 7. В обозначениях леммы 6 отображение представляется в виде , где - инъективное полуаффинное отображение; отсюда вытекает, что полуаффинно.

Доказательство. Существование и инъективность вытекают из того, что соотношение равносильно (см. лемму 5), и тем самым . Для доказательства полуаффинности покажем, что оно удовлетворяет условиям теоремы 8.1.

Пусть – произвольная аффинная прямая , порожденная двумя различными элементами из . Без труда проверяется, что есть ЛАМ в , порожденное .

По лемме 3, есть ЛАМ, порожденное ; итак (в силу инъективности ), является аффинной прямой .

Наконец, не может сводиться к одной точке или прямо, так как тогда к точке или прямой сводилось бы и , что противоречит условию 2). Поэтому .

Отсюда следует, что удовлетворяет условиям 1) и 2), наложенным на , при условии замены на . Лемма 4 показывает тогда, что образы при отображении двух параллельных прямых , из - две параллельные прямые. Наконец, удовлетворяет всем условиям теоремы 8.1 (после замены на ). Следовательно, полуаффинно и так же обстоит дело с .

Теорема 9.1 тем самым полностью установлена.

Этот результат особенно интересен в случае, когда тела и совпадают и не допускают других автоморфизмов, кроме тождественного (например, когда или при : в этом случае мы получаем чисто геометрическую характеризацию аффинных отображений ранга пространства в .

Кроме того, очевидно, что теорема 9.1 потеряла бы силу при отсутствии условия 2): ведь любое отображение на прямую тривиальным образом удовлетворяет условию 1).

Так же и в случае условие 1) выполнено для любого отображения в (поскольку каждая прямая в и состоит из двух точек). Теорема 9.1 теряет силу и в этом случае.

Наконец, нельзя заменить требование «образ прямой есть прямая или точка» более слабым условием «образы коллинеарных точек коллинераны», даже при условии, что биективно.

Например, , есть биекция векторного пространства над в векторное пространство над , и образ каждой прямой из при отображении содержится в фнекоторой прямой пространства , но не является полулинейным (поскольку и не изоморфны).

Тогда имеет единственную аффинную структуру, такую, что каноническая проекция является аффинной.

По лемме 3, есть ЛАМ, порожденное ; итак (в силу инъективности ), является аффинной прямой .

Теорема 9.1 тем самым полностью установлена.

Например, , есть биекция векторного пространства над в векторное пространство над , и образ каждой прямой из при отображении содержится в некоторой прямой пространства , но не является полулинейным (поскольку и не изоморфны).