
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Сборник Лекций 2 по Мат.Анализу
Реферат: Сборник Лекций 2 по Мат.Анализу
Глава 3. Функция нескольких переменных
§1. Основные понятия
Пусть имеется n+1 переменная x1, x2, ..., xn, y, которые связаны между собой так, что каждому набору числовых значений переменных x1, x2, ..., xn соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x1, x2, ..., xn называется значением функции f в точке (x1, x2, ..., xn), что записывается в виде формулы y = f(x1,x2,..., xn) или y =y(x1,x2,..., xn).
Переменные x1, x2, ..., xn являются аргументами этой функции, а переменная y функцией от n переменных.
Далее будем говорить лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать как правило x и y, а значение функции z.
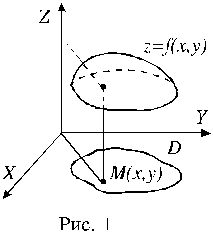
Множество D называется областью определения функции.
Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f(x,y) можно писать z=f(M).При этом аргументами функции будут координаты x,y точки M.
Числа
x,y
можно рассматривать
как координаты
вектора
![]() ,
исходящего
из начала координат
и с концом в
точке M(x,y).
Тогда функция
двух переменных
будет функцией
вектора,
что записывается
в виде формулы
z = f(
,
исходящего
из начала координат
и с концом в
точке M(x,y).
Тогда функция
двух переменных
будет функцией
вектора,
что записывается
в виде формулы
z = f(![]() ),
причем аргументами
функции являются
координаты
вектора
),
причем аргументами
функции являются
координаты
вектора ![]() .
.
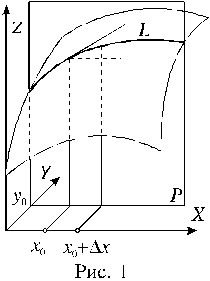
График функции двух переменных есть множество точек (x,y,f(x,y)), где (x,y)D. График представляет собой некоторую поверхность. Пример такой
поверхности приводится на рисунке 1.
Одним из подходов к исследованию функций двух переменных является изучение поведения функции в точке, то есть определение направлений, в которых функция убывает или возрастает, и определение скорости возрастания или убывания.
Можно использовать другой подход. Пусть имеется функция z = f(x,y) c графиком, представляющим собой некоторую поверхность.
В микроэкономике, в предположении что потребитель приобретает лишь два вида товаров: A и B, вводится понятие общей полезности TU, как функции двух аргументов: Q1 и Q2 – количеств потребленных товаров A и B, соответственно:
TU = TU(Q1,Q2). (1)
Очевидно, что все линии уровня функции TU(Q1,Q2) составляют семейство кривых безразличия (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 125).
Пусть в плоскости XOY заданы две точки: M0(x0,y0) и M1(x1,y1). Расстояние между этими точками рассчитывается по формуле
![]() . (2)
. (2)
Пусть некоторое положительное число. -окрестностью V точки M0(x0,y0) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам
![]() .
.
Очевидно, что -окрестность точки M0(x0,y0) представляет собой круг радиуса с выколотым центром.
Точка M0(x0,y0) называется точкой минимума функции z = f(x,y), если существует такое положительное число , что из условия M(x,y) V (x0,y0) следует f(x,y) > f(x0,y0).
Точка M0(x0,y0) называется точкой максимума функции z = f(x,y), если существует такое положительное число , что из условия M(x,y) V (x0,y0) следует: f(x,y) < f(x0,y0).
Точки минимума и максимума называются точками экстремума.
Число A называется пределом функции z = f(x,y) в точке M0(x0,y0):
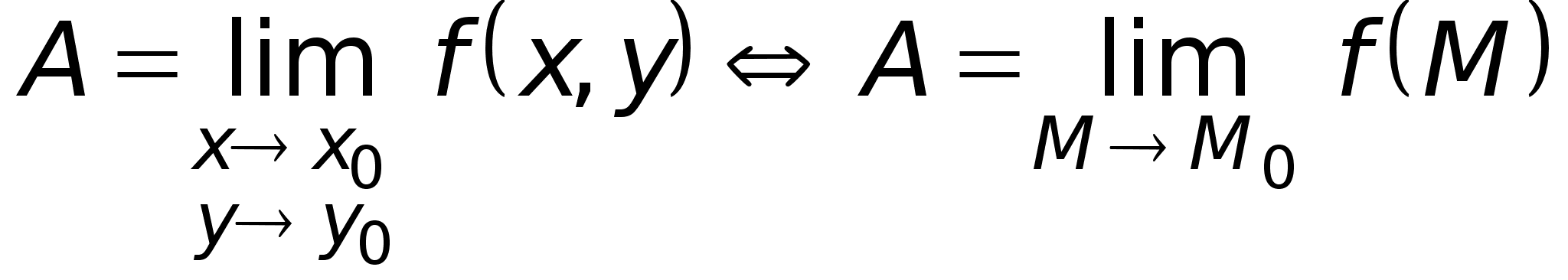 ,
,
если для произвольного числа > 0 найдется такое число > 0, что для всех точек M(x,y) из -окрестности точки M0(x0,y0) выполняется неравенство
|f(x,y) - A| .
Функция z = f(x,y) называется непрерывной в точке M0(x0,y0), если
![]() .
.
Два последних определения фактически повторяют определения предела и непрерывности в точке для функции одной переменной.
§2. Частные производные
Частной производной по x функции z = f(x,y) в точке M0(x0,y0) называется предел
![]()
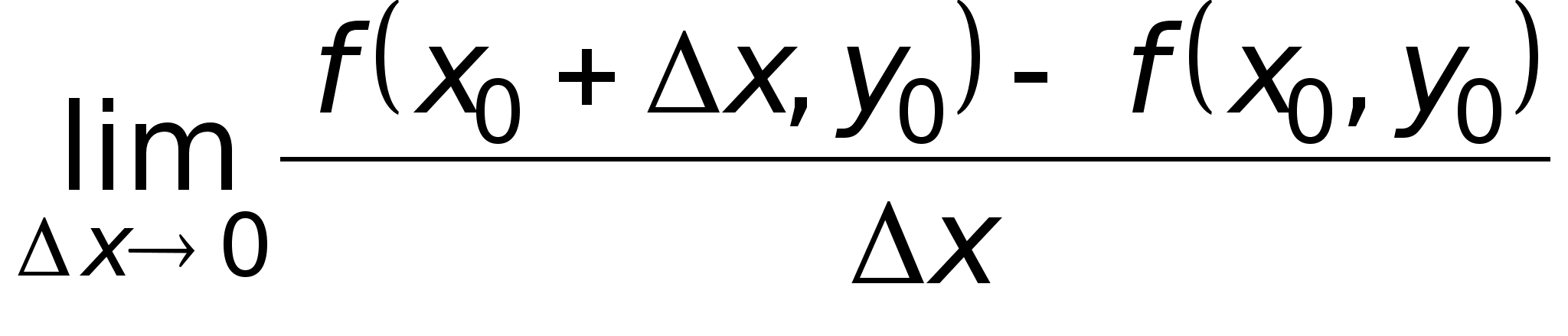 ,
,
если этот предел существует. Обозначается эта частная производная любым из следующих символов:
![]() ;
;![]() ;
;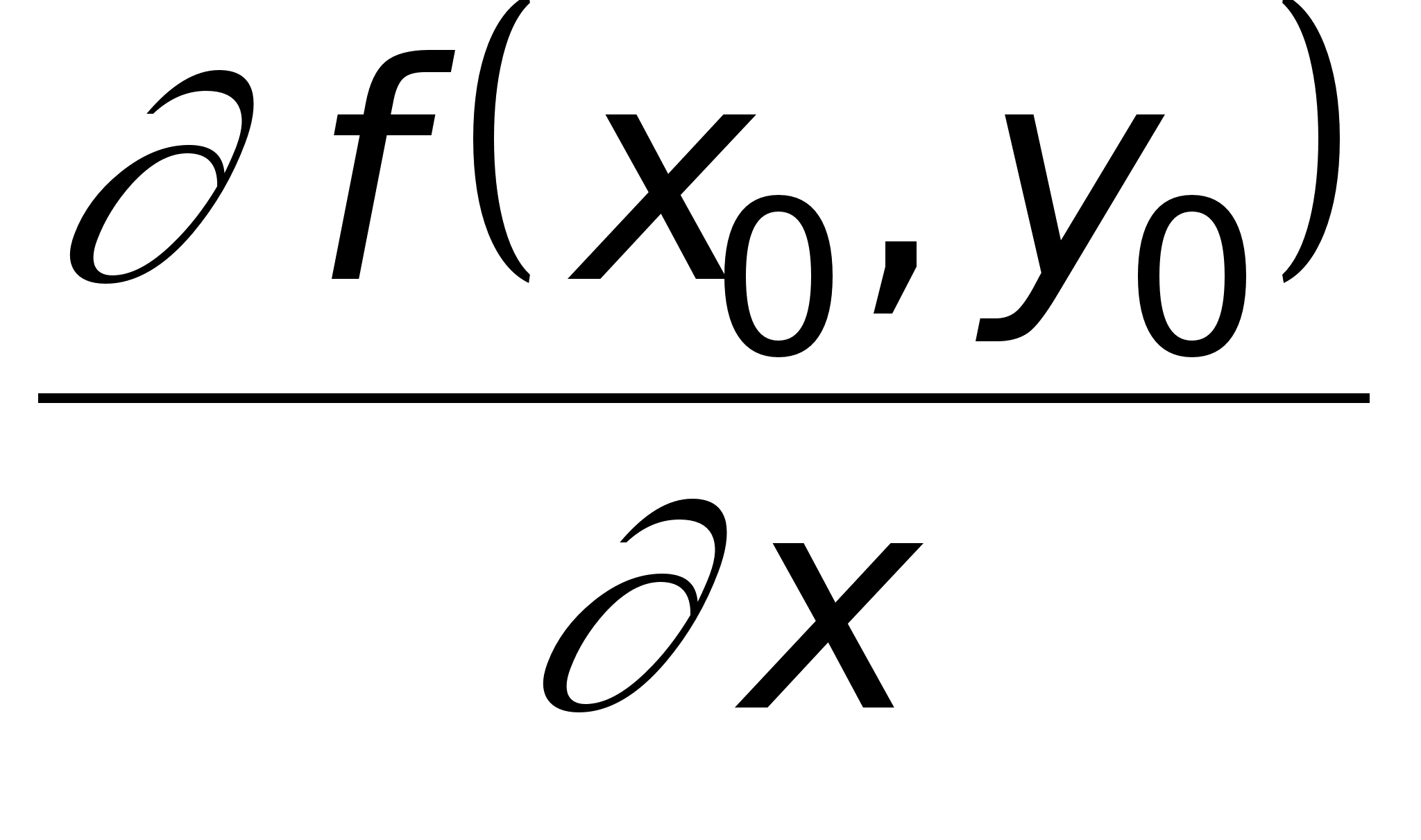 .
.
Частная производная по x есть обычная производная от функции z = f(x,y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функции z = f(x,y) в точке M0(x0,y0):
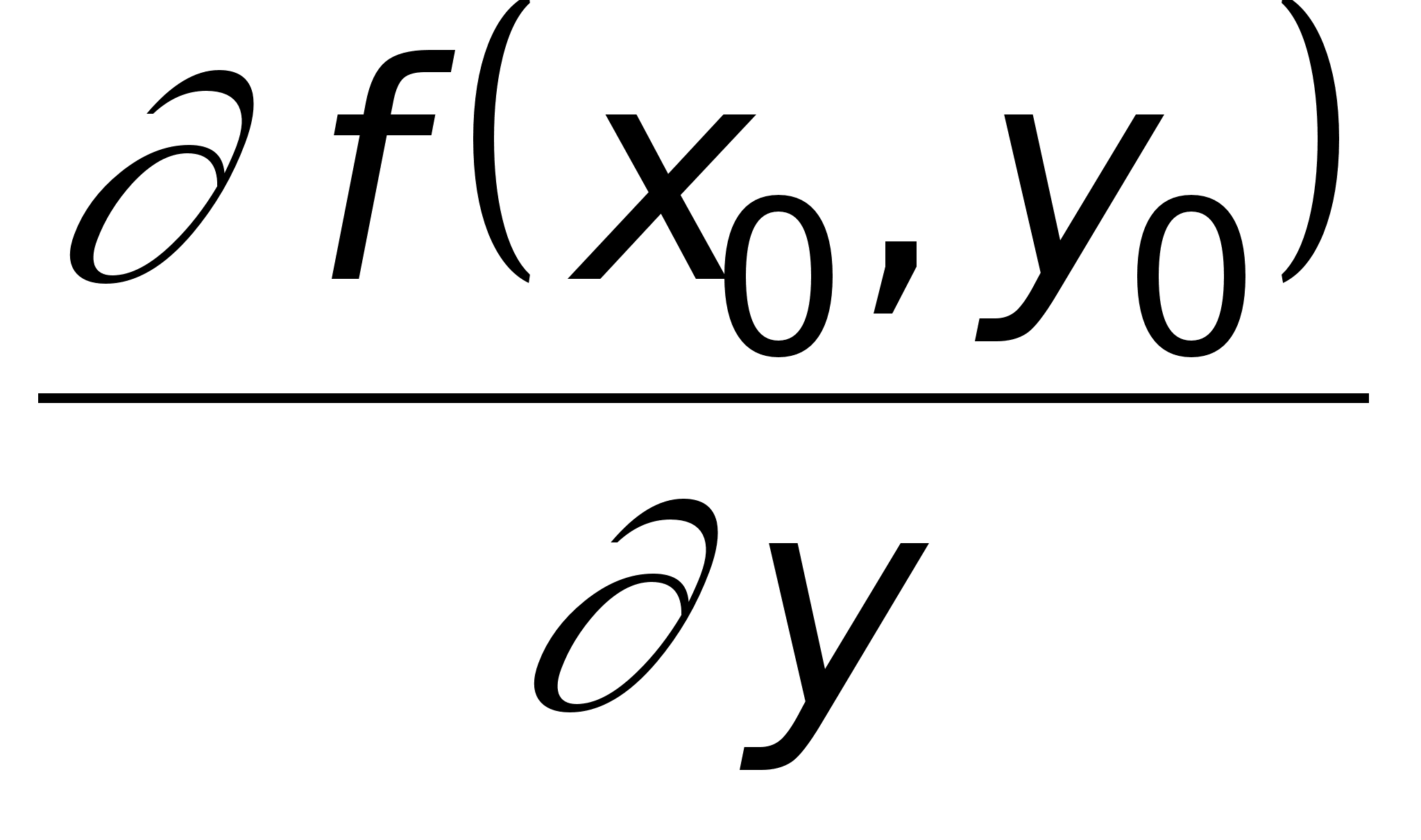 =
=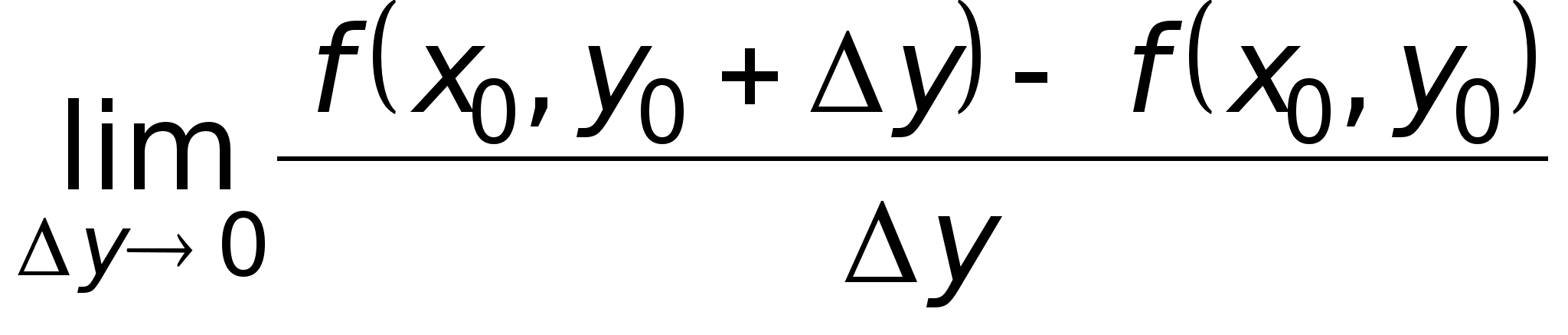 .
.
Аналогичное заключение можно сделать относительно частной производной по y.
Приведем примеры вычисления частных производных. Как говорилось выше, для вычисления частной производной по x функции z = f(x,y) нужно положить переменную y равной константе, а при нахождении частной производной по y нужно считать константой переменную x.
Примеры.
1.
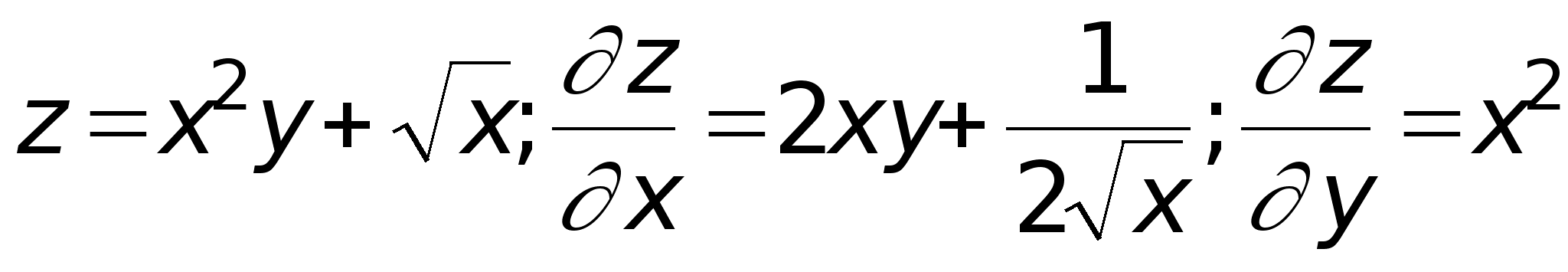 .
.
2.
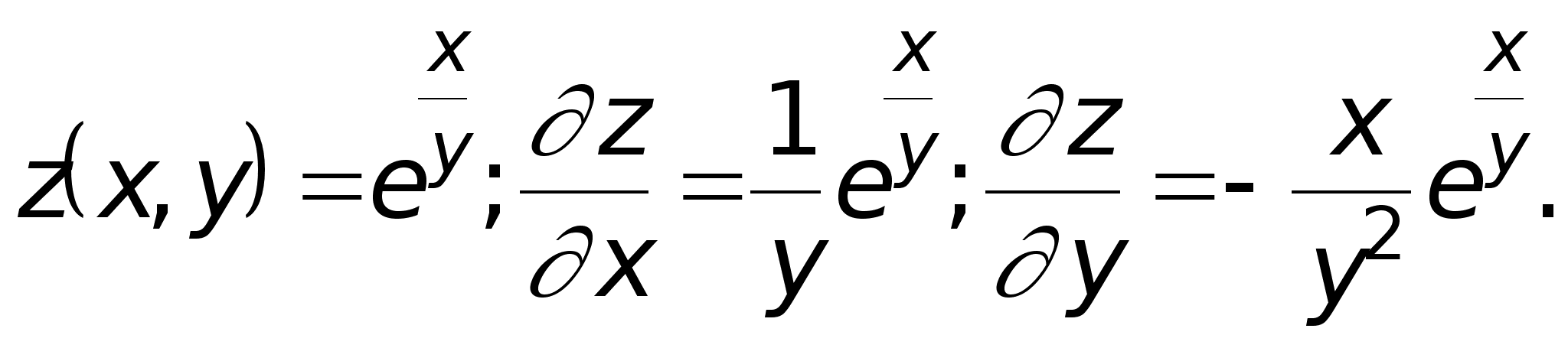
Если частные производные функции z = f(x,y) существуют на некотором множестве, а точка, в которой вычисляются частные производные несущественна, то пользуются более короткими обозначениями:
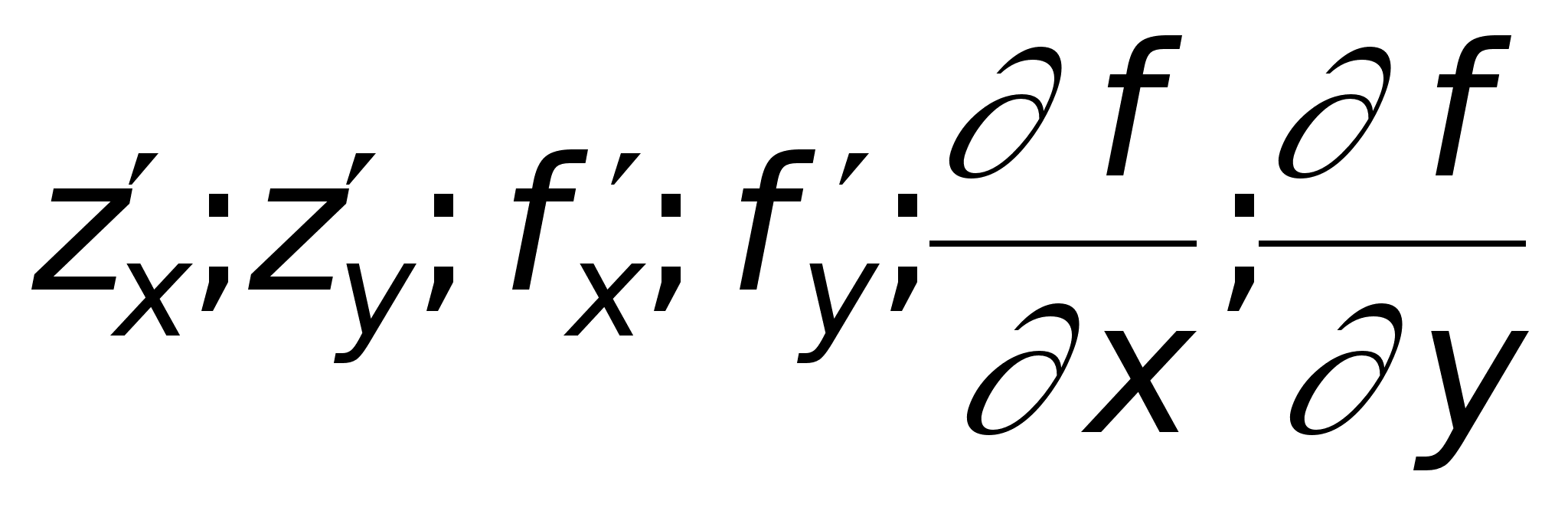 .
.
Сами
частные производные
могут являться
функциями от
нескольких
переменных
на некотором
множестве. У
этих функций
тоже могут
существовать
частные производные
по x
и по y.
Они называются
вторыми частными
производными
или частными
производными
второго порядка
и обозначаются
zxx, zyy, zxy
или
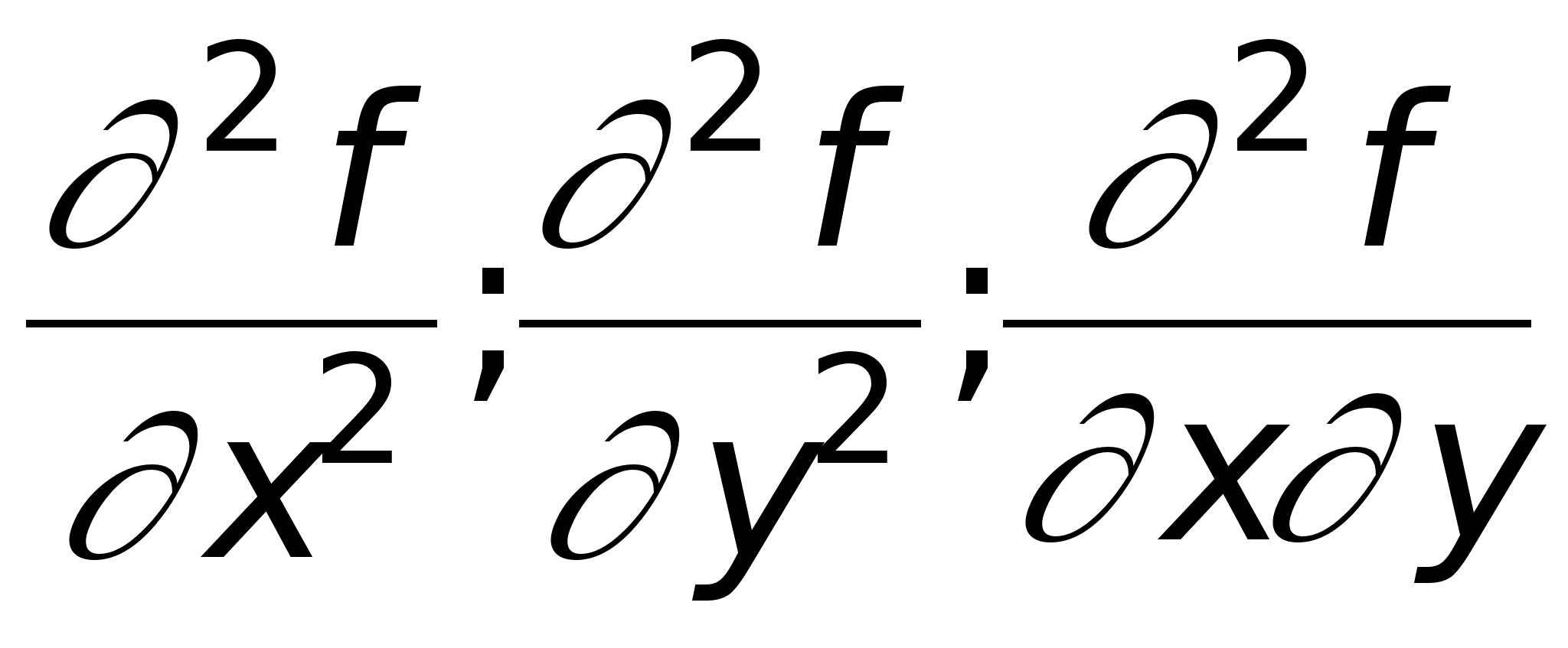 .
Согласно определению
.
Согласно определению
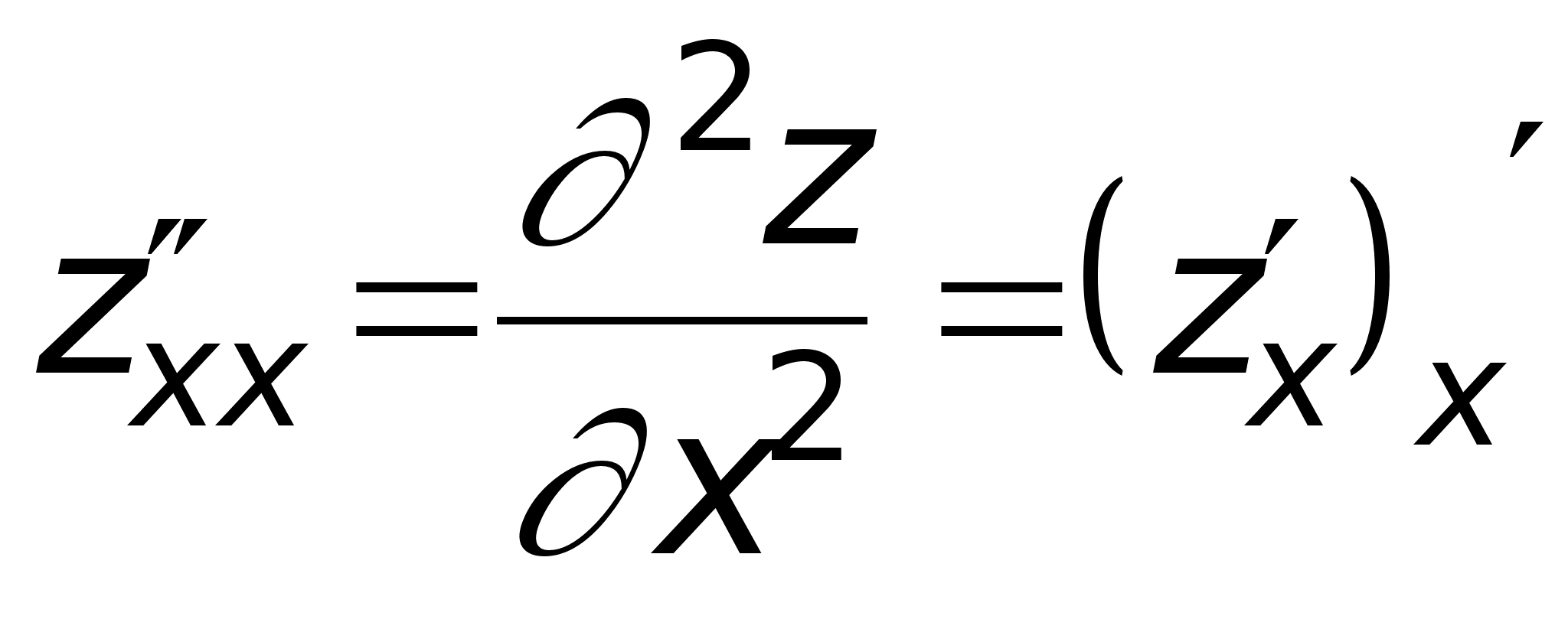 ;
;
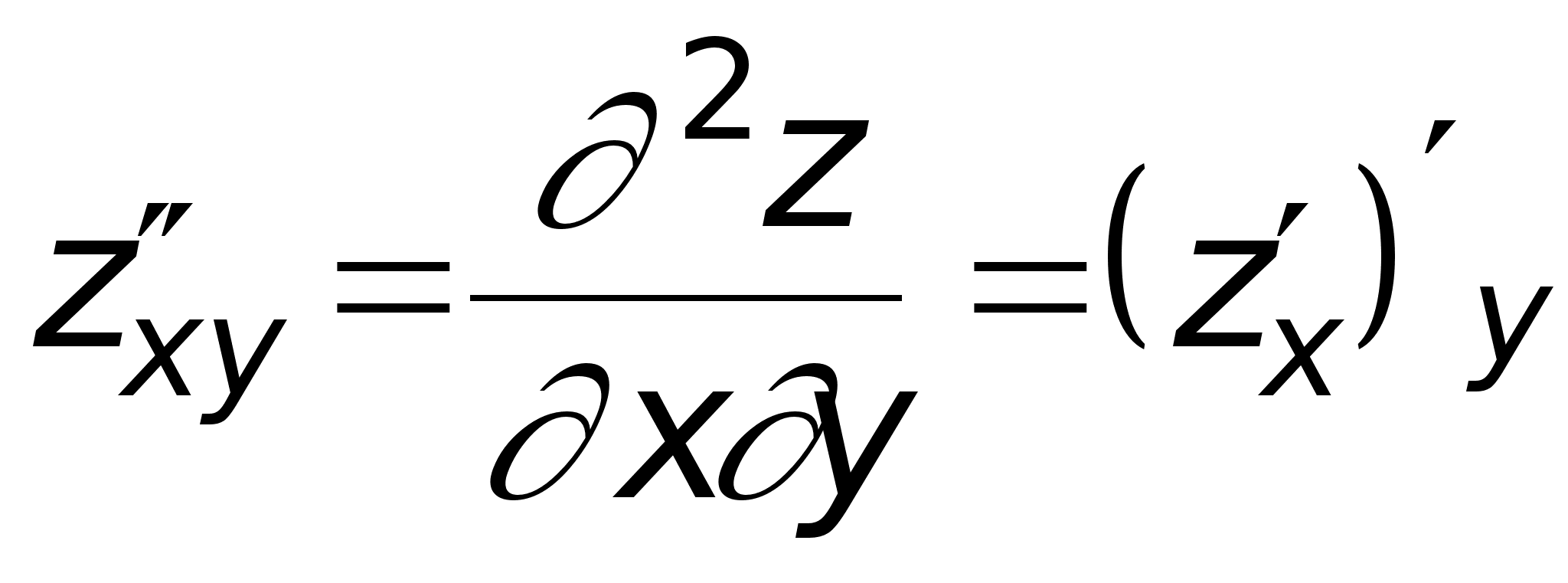 .
Последняя
частная производная
второго порядка
называется
смешанной.
Смешанная
частная производная
второго порядка,
вообще говоря,
зависит от
того, в какой
последовательности
берутся переменные,
по которым
вычисляется
производная.
Так,
производная
zxy = (zx
)y
может не быть
равной zyx = (zy
)x.
Однако существует
теорема, утверждающая,
что если
смешанные
частные производные
второго порядка
непрерывны,
то они не зависят
от того, в какой
последовательности
вычислялись
частные производные
по x
и по y.
(Рекомендуем
читателю самому
убедиться в
справедливости
этой теоремы
для функций,
рассмотренных
в приведенных
выше примерах
1 и 2.)
.
Последняя
частная производная
второго порядка
называется
смешанной.
Смешанная
частная производная
второго порядка,
вообще говоря,
зависит от
того, в какой
последовательности
берутся переменные,
по которым
вычисляется
производная.
Так,
производная
zxy = (zx
)y
может не быть
равной zyx = (zy
)x.
Однако существует
теорема, утверждающая,
что если
смешанные
частные производные
второго порядка
непрерывны,
то они не зависят
от того, в какой
последовательности
вычислялись
частные производные
по x
и по y.
(Рекомендуем
читателю самому
убедиться в
справедливости
этой теоремы
для функций,
рассмотренных
в приведенных
выше примерах
1 и 2.)
Отметим очень важное отличие функции двух переменных от функции одной переменной. Из существования первых частных производных в точке не следует непрерывность функции в этой точке. Рассмотрим, например, функцию
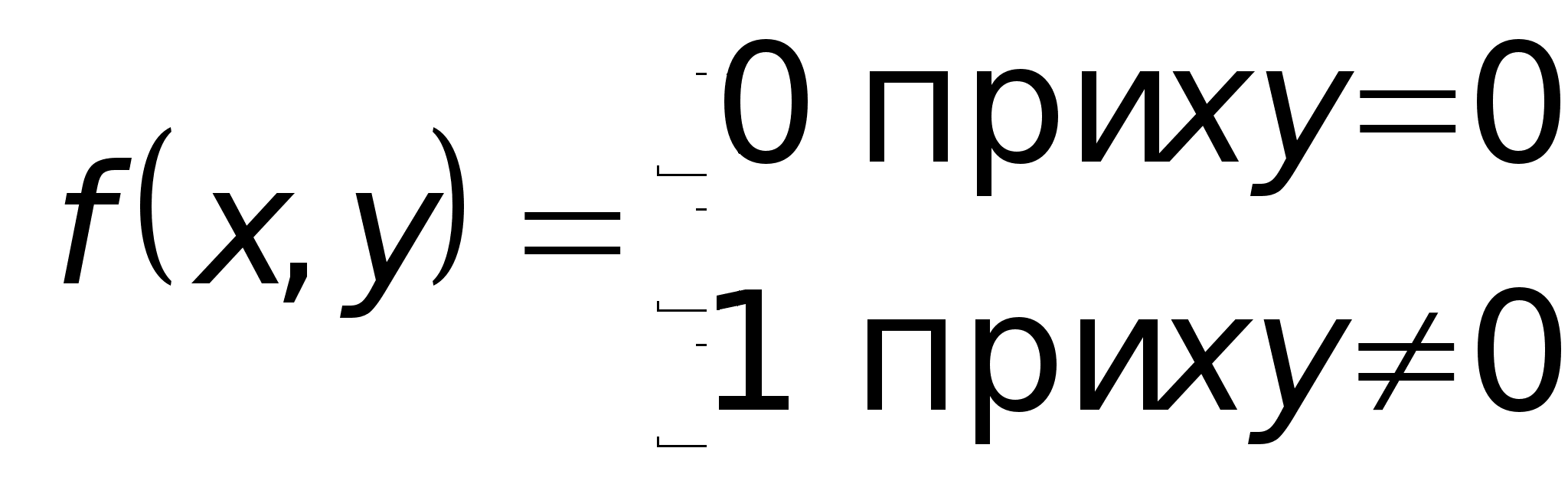 .
.
График этой функции во всех точках, не принадлежащих осям координат OX и OY, представляет собой плоскость, параллельную плоскости XOY, поднятую на 1. Сами эти оси координат также принадлежат графику рассматриваемой функции. Очевидно, что в точке (0,0) функция имеет частные производные по обоим аргументам, обе равные нулю. Очевидно также, что в любой окрестности точки (0,0) можно найти точку M такую, что f(M) = 1, в то время как f(0, 0) = 0. Это означает существование разрыва функции в точке (0,0). (Пример взят из книги О.С.Ивашева-Мусатова “Начала математического анализа”).
84
§3. Дифференциал функции двух переменных
Рассмотрим функцию z = f(x,y), имеющую в точке Р0(х0,у0) частные производные fx(х0,у0) и fу(х0,у0). Перейдём от точки Р0 к точке R0(x0+x,y0+у), придавая переменным х и у в точке Р0 произвольные приращения x и у, соответственно. При этом функция в точке Р0 получит приращение
f(х0,у0) = f(x0+x,y0+y) – f(x0,y0) = f(R0) – f(P0).
Если приращение функции f(x,y) можно представить в виде
f(х0,у0) = fx(х0,у0)x + fу(х0,у0)у + (x;у) x + (x;у)у, (1)
где
![]() ,
то функция
называется
дифференцируемой
в
точке Р0(х0,у0).
Сумма первых
двух слагаемых
в правой части
равенства (1)
называется
дифференциалом
функции f(x,y)
в точке Р0
и обозначается
df(x0,y0):
,
то функция
называется
дифференцируемой
в
точке Р0(х0,у0).
Сумма первых
двух слагаемых
в правой части
равенства (1)
называется
дифференциалом
функции f(x,y)
в точке Р0
и обозначается
df(x0,y0):
df(x0,y0) = fx(х0,у0)x + fу(х0,у0)у. (2)
Если точка, в которой вычисляется дифференциал не существенна, его принято обозначать просто df. Из определения следует, что дифференциал представляет собой главную часть приращения функции, линейную относительно приращений её аргументов. Полагая поочерёдно f(x,y) = х и f(x,y) = у, получим, что дифференциалы dх и dy независимых аргументов функции х и у равны соответственно x и у . Таким образом
df = fx dх + fу dу.
Раньше говорилось о том, что из существования частных производных в точке не следует непрерывности функции в этой точке. Однако, из справедливости равенства (1) следует
![]() ,
,
а это означает непрерывность функции в точке (х0,у0). Следовательно, дифференцируемая в точке функция обязательно непрерывна в этой точке.
Из сказанного следует, что существование обеих частных производных функции в точке не означает, что функция дифференцируема в этой точке. В курсе математического анализа доказывается теорема, что функция дифференцируема в точке, если обе частные производные этой функции непрерывны в этой точке.
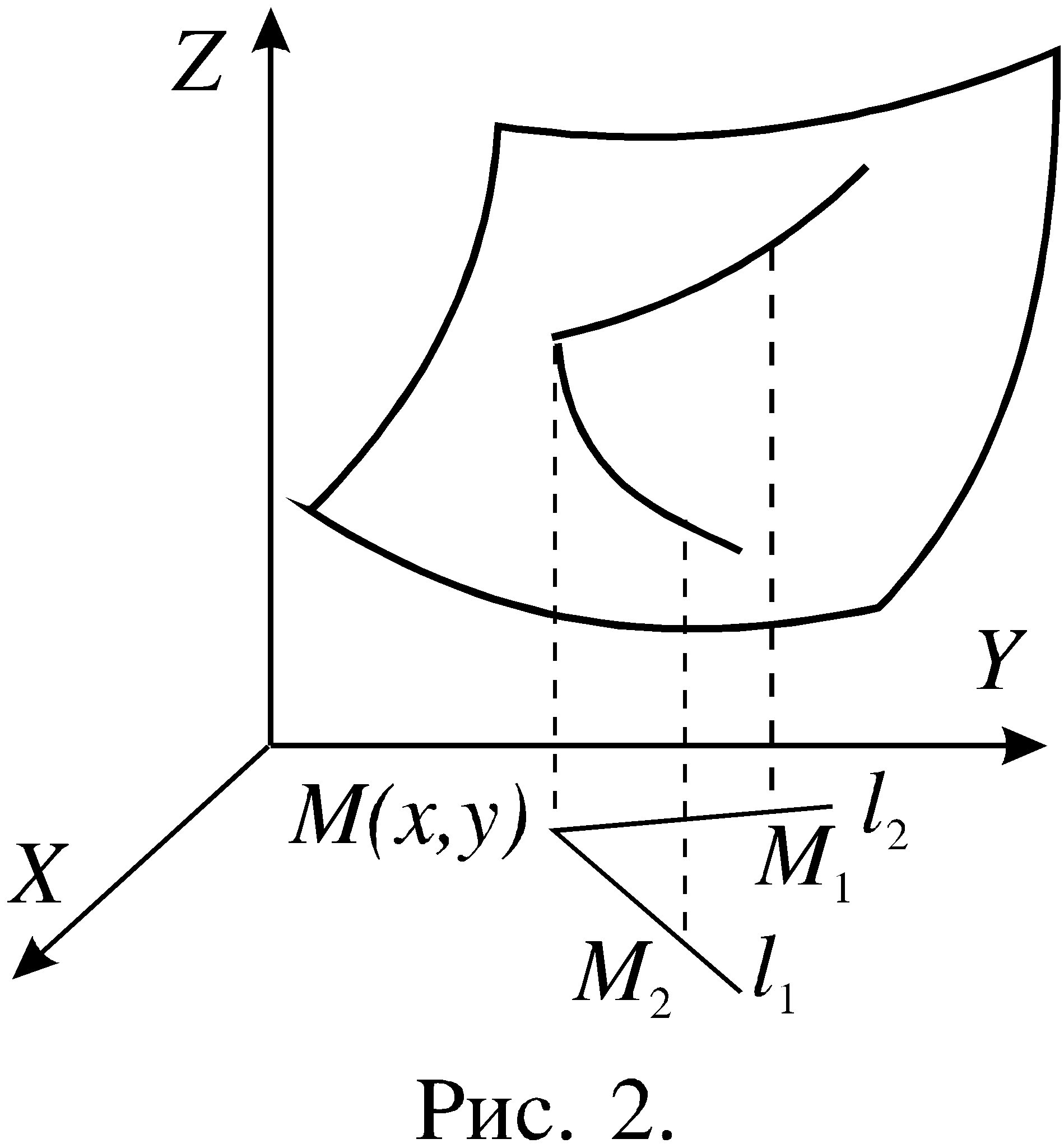
На рисунке 1 график функции z = f(x,y) представляет собой поверхность F. Длина отрезка Р0Р равна значению функции z в точке P0,
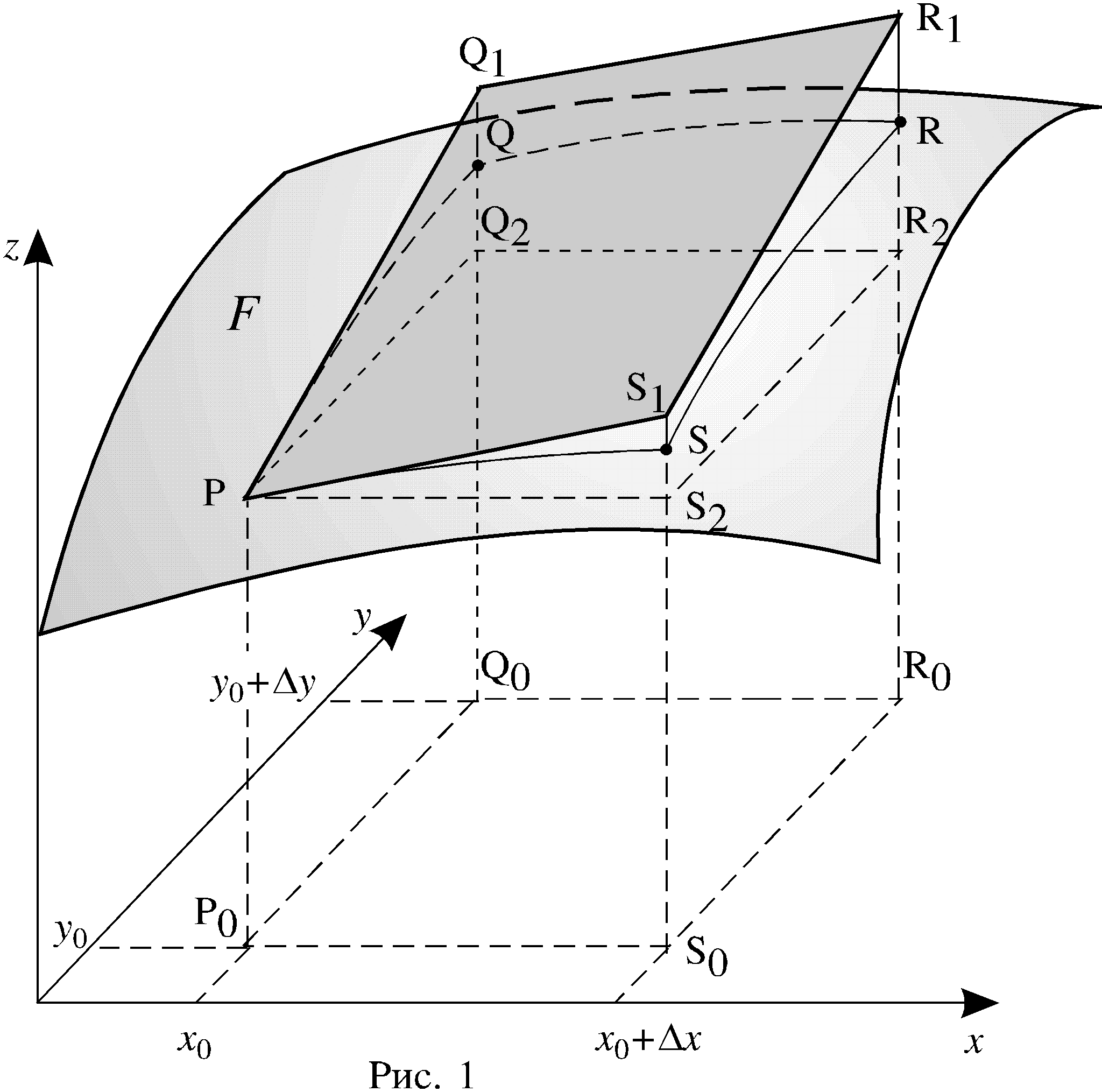
то есть Р0Р = f(x0,y0) (на рисунке для наглядности поверхность F выбрана так, что все рассматриваемые значения функции и приращения в точке P0 положительны, но это не ограничивает справедливости приведенных выше выводов и формул в общем случае). Координатами точек Q0, S0 и R0 являются пары чисел соответственно (x0,y0+у); (x0+x,y0) и (x0+x,y0+у), причём Q0Q = f(Q0), S0S = f(S0) и R0R = f(R0). Приращение f(х0,у0) функции в точке Р0 равно RR2.
Параллелограмм PQ1R1S1 лежит в плоскости, которая касается поверхности F в точке Р. Прямоугольник PQ2R2S2 расположен в горизонтальной плоскости. Очевидно: Q2Q1 = fy(x0,y0)y и S2S1 = fx(x0,y0)x.
Из легко доказываемого равенства
R2R1 = S2S1 + Q2Q1
и формулы (2) следует, что дифференциал функции в точке Р0 равен R2R1.
Так как df(x0,y0) f(x0,y0), дифференциал df даёт приближенное значение приращения функции при малых значениях приращений аргументов.
88
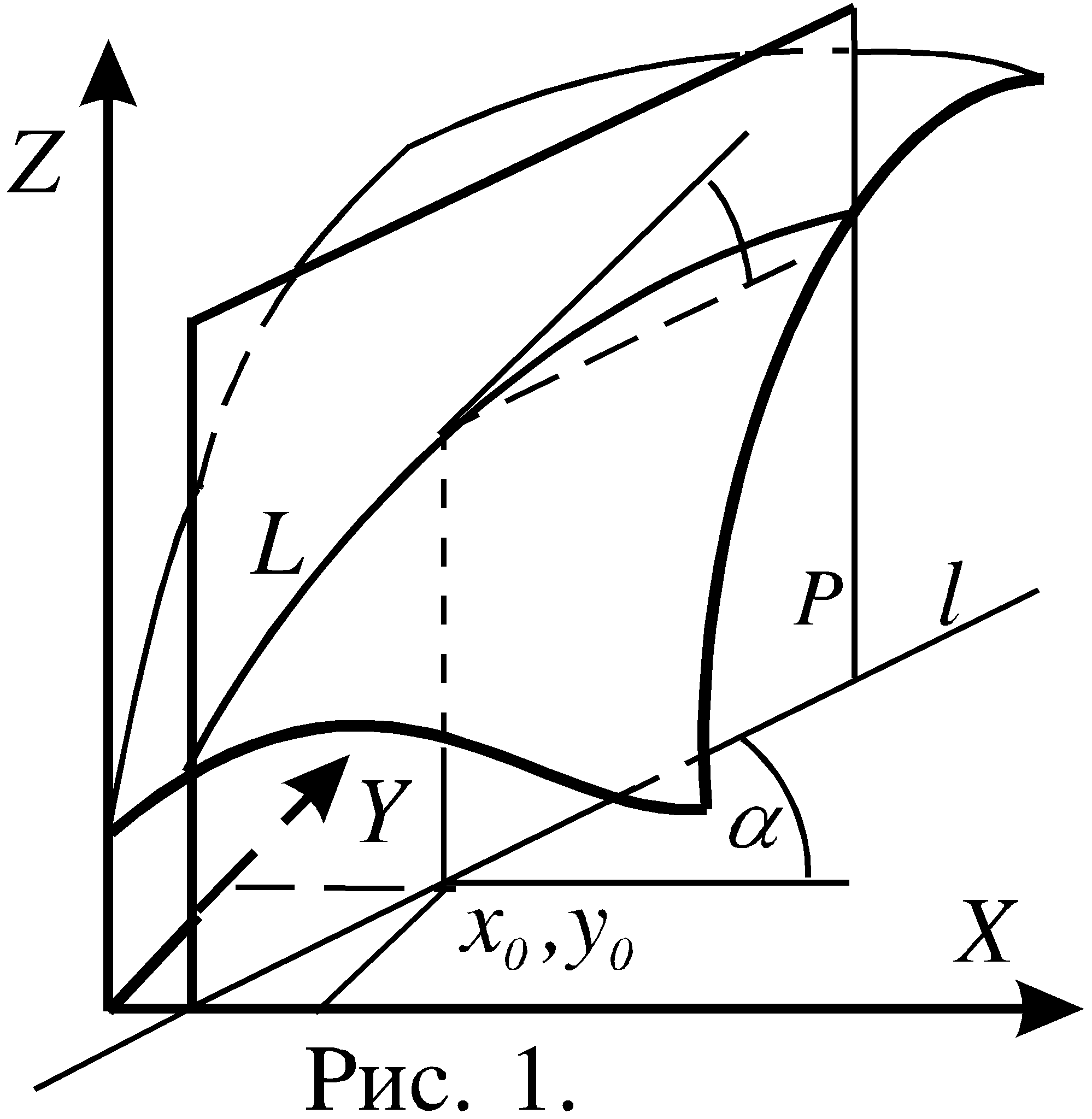
§4. Производная по направлению.
Пусть в плоскости XOY расположена точка M0(x0,y0). Зададим произвольный угол и рассмотрим множество точек на той же плоскости, координаты которых определяются из формул
x = x0 + t cos, y = y0 + t sin. (1)
Здесь t параметр, который может быть равен любому числу. Из формул (1) следует:
(y - y0)/(x - x0) = tg
Это означает, что все точки M(x,y), координаты которых удовлетворяют равенствам (1), лежат на прямой, проходящей через точку M0(x0,y0) и составляющей угол с осью OX. Каждому значению t соответствует единственная точка M(x,y), лежащая на этой прямой, причем согласно формуле (1) из §1 расстояние между точками M0(x0,y0) и M(x,y) равно t. Можно считать эту прямую числовой осью с положительным направлением, определяемым возрастанием параметра t. Обозначим положительное направление этой оси символом l.
Производной функции z = f(x,y) в точке M0(x0,y0) по направлению l называется число
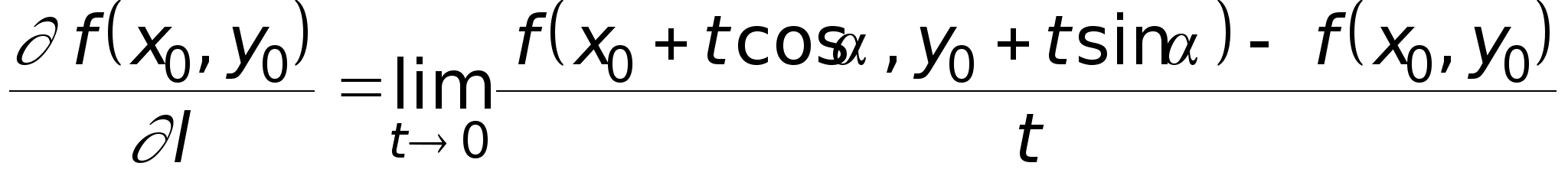 . (2)
. (2)
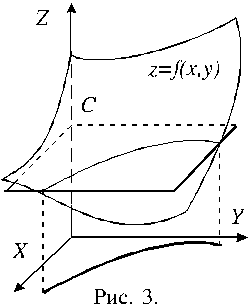
Производной функции по направлению можно дать геометрическую интерпретацию. Если через прямую l, определяемую формулами (1), провести вертикальную плоскость P (на самом деле в трехмерном пространстве уравнения (1) определяют эту самую плоскость), то эта плоскость пересечет поверхность-график функции z = f(x,y) вдоль
![]() В
любом курсе
математического
анализа доказывается,
что производная
по направлению,
определяемая
формулой (2), может
быть представлена
в виде
В
любом курсе
математического
анализа доказывается,
что производная
по направлению,
определяемая
формулой (2), может
быть представлена
в виде
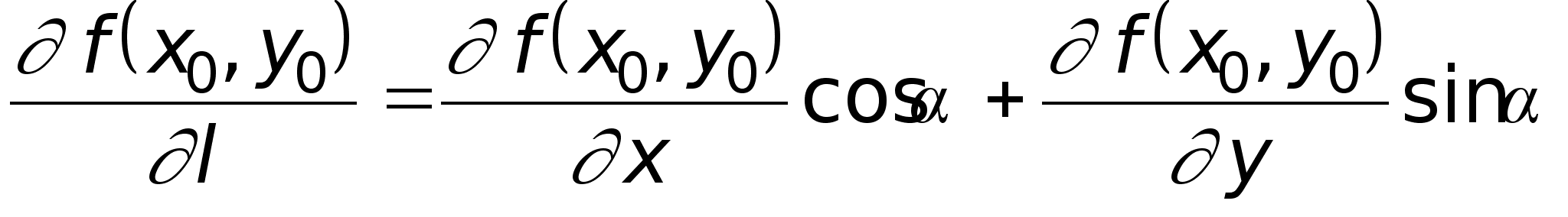 . (3)
. (3)
Заметим, что частная производная по x тоже является производной по направлению. Это направление определяется равенствами: cos = 1; sin = 0. Аналогично частная производная по y — это производная по направлению, которое можно задать условиями cos = 0; sin = 1.
Прежде,
чем анализировать
формулу (3), приведем
некоторые
понятия и факты
из курса векторной
алгебры. Пусть
в плоскости
с системой
координат XOY
задан направленный
отрезок
![]() или (что то же
самое) вектор,
причем точка
M0(x0,y0)
является
его начальной
точкой, а M1(x1,y1)
конечной точкой.
Определим
координату
вектора по оси
OX
как число, равное
x1 x0,
а координату
по оси
или (что то же
самое) вектор,
причем точка
M0(x0,y0)
является
его начальной
точкой, а M1(x1,y1)
конечной точкой.
Определим
координату
вектора по оси
OX
как число, равное
x1 x0,
а координату
по оси
![]() ,
как число, равное
y1 y0.
Если задать
упорядоченную
пару любых
чисел a
и b,
то эти числа
можно рассматривать
как координаты
некоторого
вектора
,
как число, равное
y1 y0.
Если задать
упорядоченную
пару любых
чисел a
и b,
то эти числа
можно рассматривать
как координаты
некоторого
вектора
![]() в плоскости
XOY,
причем длина
этого вектора
определена
формулой
в плоскости
XOY,
причем длина
этого вектора
определена
формулой
![]() ,
,
а тангенс угла наклона вектора к оси OX определяется из формулы tg = b/a (отметим, что зная величину tg , а также знак любого из чисел a и b, мы можем определить угол с точностью до 2 ).
Представление
вектора в виде
пары его координат
будем записывать
в виде
![]() или
или
![]() .
Такое представление
имеет одну
характерную
особенность:
оно не
определяет
местоположение
вектора на
плоскости
XOY.
Чтобы его определить,
нужно наряду
с координатами
вектора задавать,
например, координаты
его начальной
точки или, как
её можно назвать,
точки приложения
вектора.
.
Такое представление
имеет одну
характерную
особенность:
оно не
определяет
местоположение
вектора на
плоскости
XOY.
Чтобы его определить,
нужно наряду
с координатами
вектора задавать,
например, координаты
его начальной
точки или, как
её можно назвать,
точки приложения
вектора.
Если
заданы два
вектора:
![]() и
и
![]() ,
то скалярным
произведением
,
то скалярным
произведением
![]() этих векторов
называется
число
этих векторов
называется
число
![]() (
угол между
векторами).
(
угол между
векторами).
В
любом курсе
векторной
алгебры доказывается,
что скалярное
произведение
векторов
![]() и
и
![]() равно сумме
произведений
одноименных
координат этих
векторов:
равно сумме
произведений
одноименных
координат этих
векторов:
![]() = a1b1 + a2b2. (4)
= a1b1 + a2b2. (4)
Пусть
в некоторой
области G
плоскости XOY
задана
функция z = f(x,y),
имеющая непрерывные
частные производные
по обоим аргументам.
Градиентом
или вектором-градиентом
![]() функции f(x,y)
в точке (x,y) G
называется
вектор, который
задается формулой
функции f(x,y)
в точке (x,y) G
называется
вектор, который
задается формулой
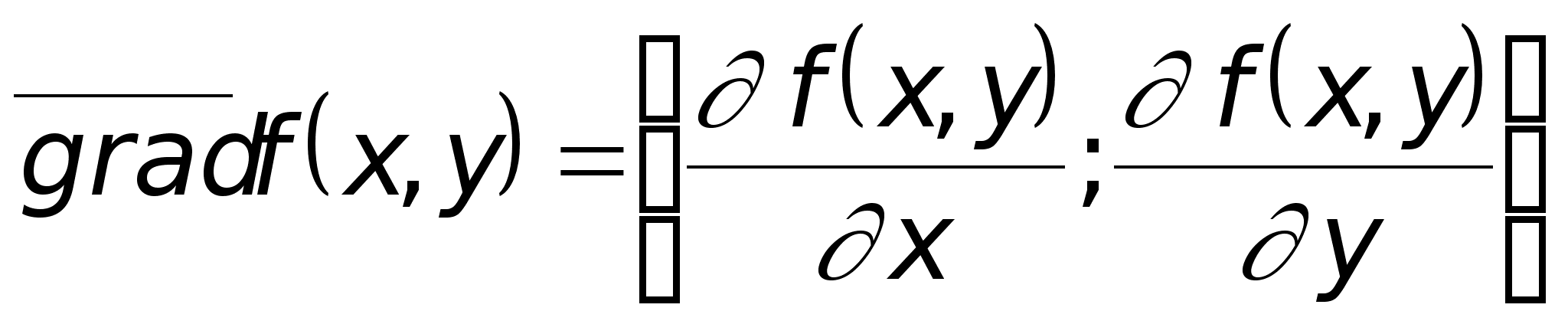 .
.
Функция f определяет для каждой точки области G вектор-градиент, исходящий из этой точки.
Возвратимся теперь к формуле (3). Ее правую часть мы можем рассматривать, как скалярное произведение векторов. Первый из них вектор-градиент функции z = f(x,y) в точке M0(x0,y0):
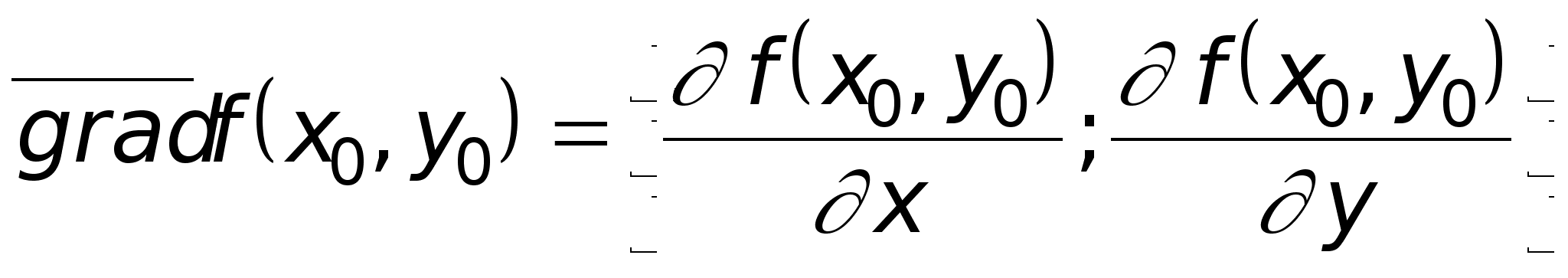 .
.
Второй
– вектор
![]() .
Это вектор,
имеющий длину
1 и угол наклона
к оси
.
Это вектор,
имеющий длину
1 и угол наклона
к оси
![]() ,
равный .
,
равный .
Теперь можно сделать вывод, что производная функции z = f(x,y) по направлению, определяемому углом наклона к оси OX, в точке M0(x0,y0) может быть вычислена по формуле
 . (5)
. (5)
Здесь
угол между
вектором
![]() и вектором
и вектором
![]() ,
задающим направление,
по которому
берется производная.
Здесь также
учтено, что
,
задающим направление,
по которому
берется производная.
Здесь также
учтено, что
![]() .
.
Из формулы (5) можно сделать очень важное заключение: производная по направлению от функции z = f(x,y) в точке M0(x0,y0) достигает наибольшего значения, если это направление совпадает с направлением вектора-градиента функции в рассматриваемой точке, так как cos 1, и равенство достигается только если = 0 (очевидно, что другие решения уравнения cos = 1 нас в данном случае не интересуют). Иначе можно сказать, что вектор-градиент функции в точке направлен в сторону наискорейшего возрастания функции в этой точке.
Кроме того из формулы (5) следует, что наибольшее значение производной по направлению в точке или наибольшее значение скорости возрастания функции в точке равно длине вектора-градиента функции в этой точке.
Пример.
Требуется найти
производную
функции
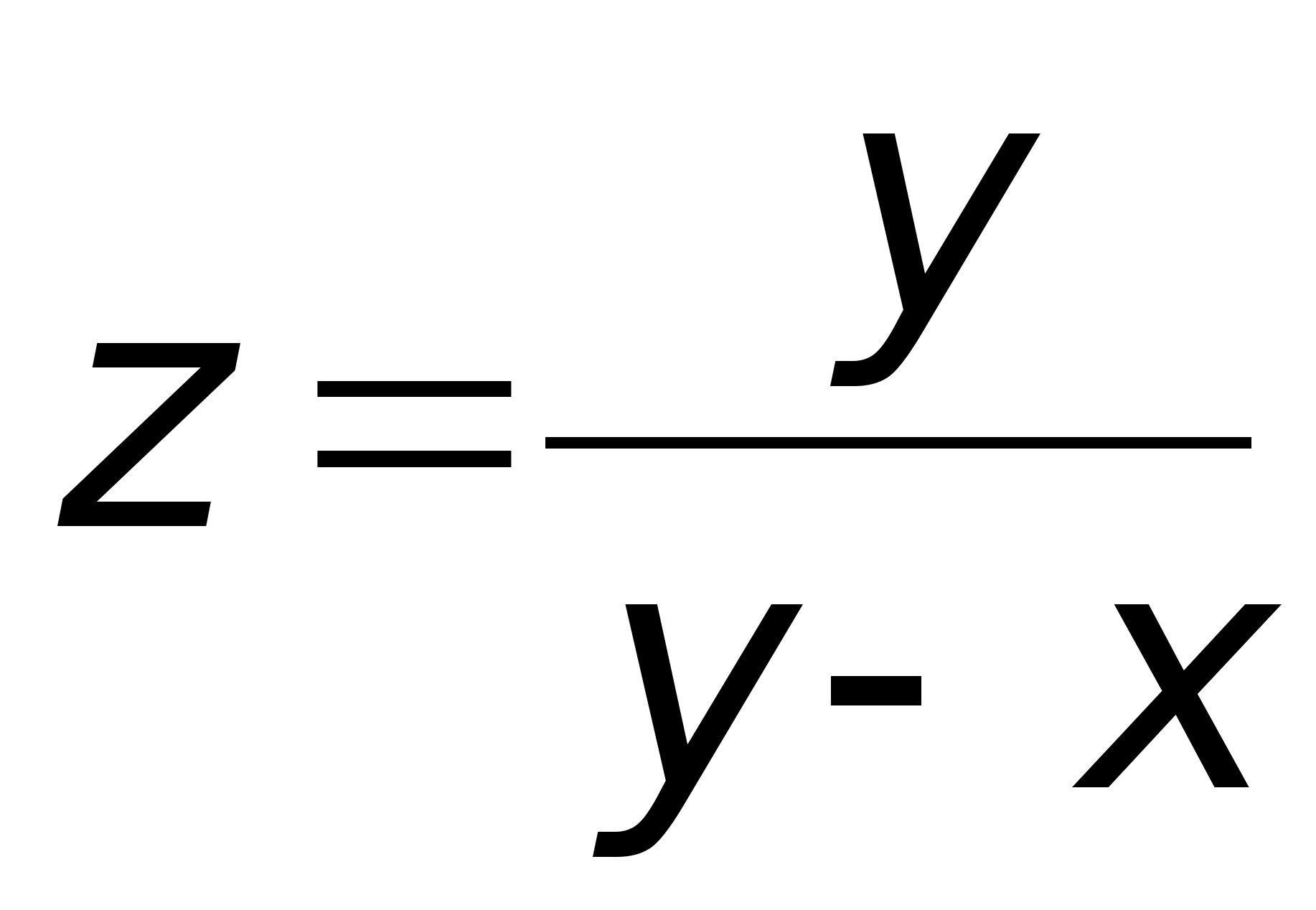 по направлению,
составляющему
угол в 60
с осью OX,
в точке (1;3).
по направлению,
составляющему
угол в 60
с осью OX,
в точке (1;3).
Найдем
частные производные
функции:
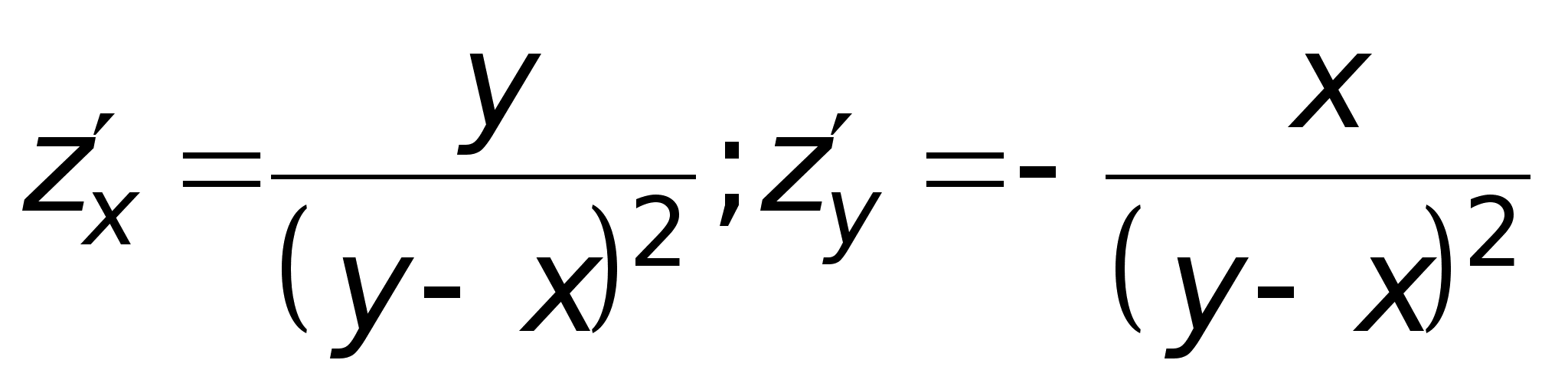 Теперь можно
определить
градиент функции
в точке (1;3):
Теперь можно
определить
градиент функции
в точке (1;3):
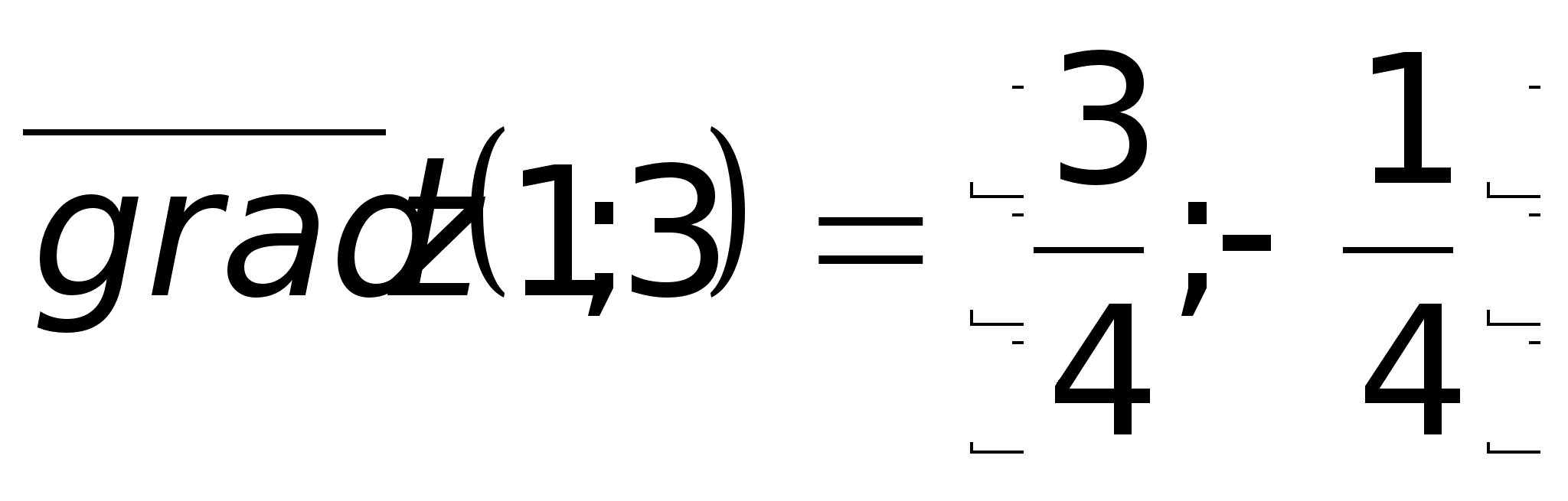 .
Принимая во
внимание равенство
.
Принимая во
внимание равенство
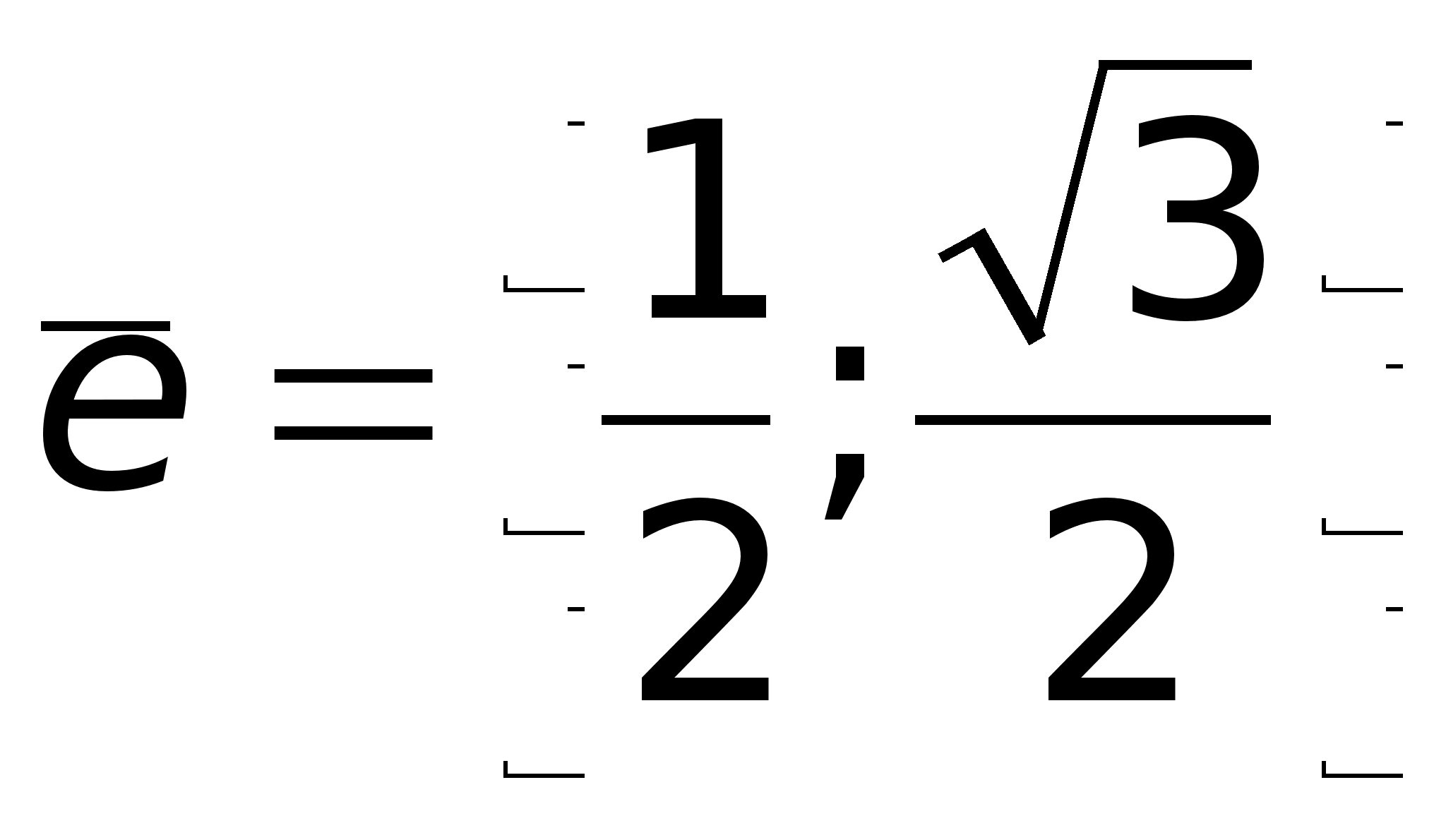 ,
воспользуемся
формулой (4):
,
воспользуемся
формулой (4):
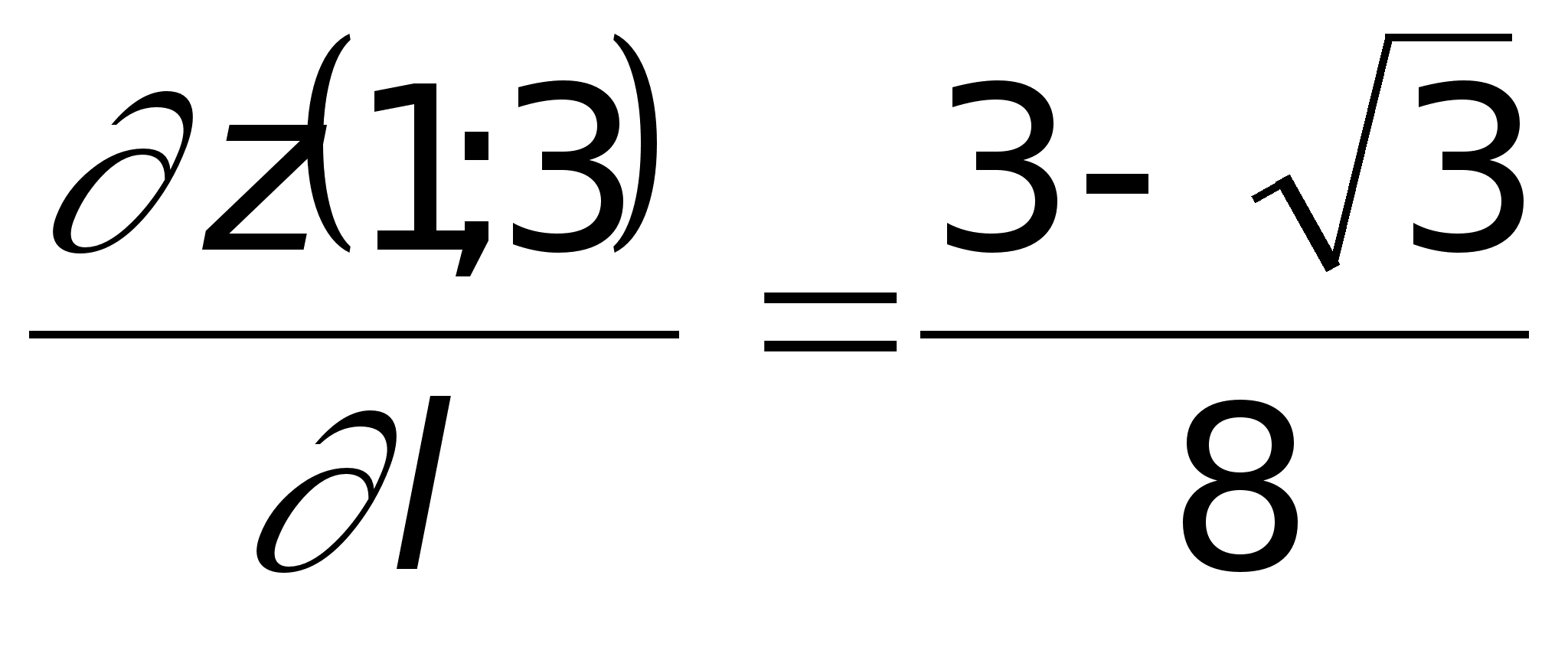 .
.
92
§5. Экстремум функции двух переменных.
Точка M0(x0,y0) является точкой максимума (минимума) функции z = f(x,y), если найдется такая окрестность точки M0, что для всех точек M(x,y) из этой окрестности выполняется неравенство f(x,y) f(x0,y0) ( f(x,y)> f(x0,y0)).
Точки максимума и минимума называются точками экстремума.
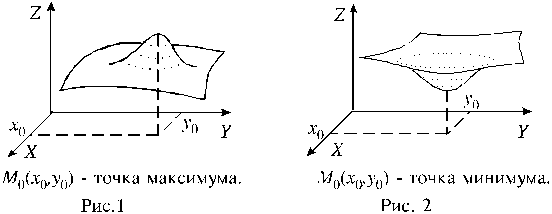
Сформулируем необходимое условие экстремума.Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.
Точки экстремума дифференцируемой функции (то есть функции, имеющей непрерывные частные производные во всех точках некоторой области) надо искать только среди тех точек, в которых все первые частные производные равны нулю.
Там, где выполняется необходимое условие, экстремума может и не быть (здесь полная аналогия с функцией одной переменной).
Пример:
z = xy; zx = y; zy = x; zx(0,0) = 0; zy(0,0) = 0.
Обе частные производные в точке (0,0) обращаются в 0. Однако точка (0,0) не является точкой экстремума, так как в ней самой z = 0, а в любой её окрестности есть точки, где z(x,y) > 0 (это точки, лежащие внутри первого и третьего координатных углов), и есть точки, где z(x,y) < 0 (это точки, лежащие внутри второго и четвертого координатных углов).
Для ответа на вопрос, является ли точка области определения функции точкой экстремума, нужно использовать достаточное условие экстремума. Ниже приводится его формулировка.
Пусть zx(x0,y0) = 0 и zy(x0,y0) = 0, а вторые частные производные функции z непрерывны в некоторой окрестности точки (x0,y0). Введем обозначения: A = zxx(x0,y0); B = zxy(x0,y0); C = zyy(x0,y0); D = AC - B2.
Тогда, если D < 0, то в точке (x0,y0) экстремума нет.
Если D > 0, то в точке (x0,y0) экстремум функции z, причем если A > 0, то минимум, а если A < 0, то максимум.
Если D = 0, то экстремум может быть, а может и не быть. В данном случае требуются дополнительные исследования.
Исследование функции двух переменных на экстремум сводится к следующему: сначала выписываются необходимые условия экстремума:
zx(x,y) = 0;
zy(x,y) = 0
которые рассматриваются как система уравнений. Ее решением является некоторое множество точек. В каждой из этих точек вычисляются значения D и проверяется выполнение достаточных условий экстремума.
§6. Метод наименьших квадратов
Пусть проводится n однородных испытаний или экспериментов, и результатом каждого испытания является пара чисел – значений некоторых переменных x и y. Испытание с номером i приводит к числам xi, yi. В качестве испытания можно, например, рассматривать выбор определенного предприятия в данной отрасли промышленности, величиной x считать объем производства продукции (например в миллионах рублей), величиной y – объем экспорта этого вида продукции (в миллионах рублей), и обследовать n предприятий отрасли.
Итогом этих испытаний является таблица:
|
|
|
|
. . . |
|
|
|
|
|
. . . |
|
В
качестве значений
![]() часто рассматриваются
моменты времени:
t1, t2, ..., tn,
взятые через
равные промежутки.
Тогда таблица
часто рассматриваются
моменты времени:
t1, t2, ..., tn,
взятые через
равные промежутки.
Тогда таблица
|
|
|
|
. . . |
|
|
|
|
|
. . . |
|
Нас интересует вопрос, как найти приближенную формулу для функции y = f(x), которая “наилучшим образом” описывала бы данные таблицы.
Пусть точки с координатами (xi,yi) группируются на плоскости вдоль некоторой прямой. Задача заключается в том, чтобы найти параметры a0 и a1 этой прямой:
y = a0 + a1x, (1)
причем это нужно сделать так, чтобы она лучше любой другой прямой соответствовала расположению на плоскости экспериментальных точек (xi, yi).
Признаком наилучшей прямой считается минимум суммы квадратов отклонений фактических значений y, полученных из таблицы, от вычисленных по формуле (1). Эта сумма квадратов рассчитывается по формуле
S2 = (y1 – (a0 + a1x1))2 + (y2 – (a0 + a1x2))2 +...+ (yn – (a0 + a1xn))2 =
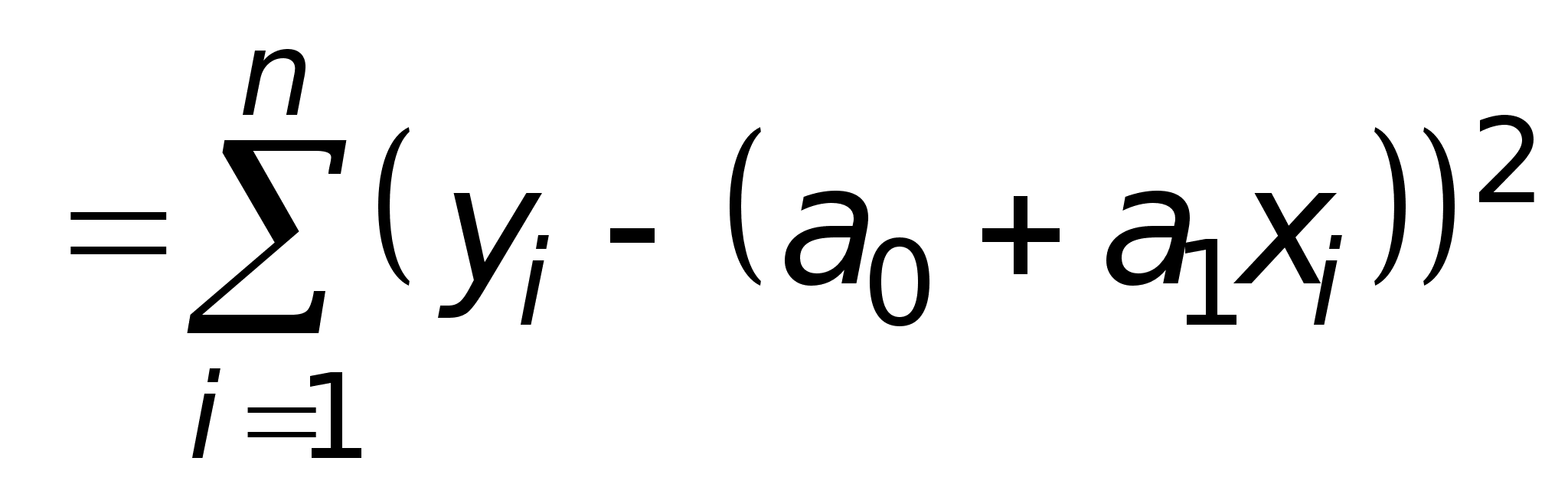 .
.
Обратим внимание на то, что все xi и yi — известные из таблицы числа, а S2 есть функция двух переменных a0 и a1.
S2 = S2(a0,a1)
Отсюда следует, что точку минимума можно искать, используя лишь необходимые условия экстремума:
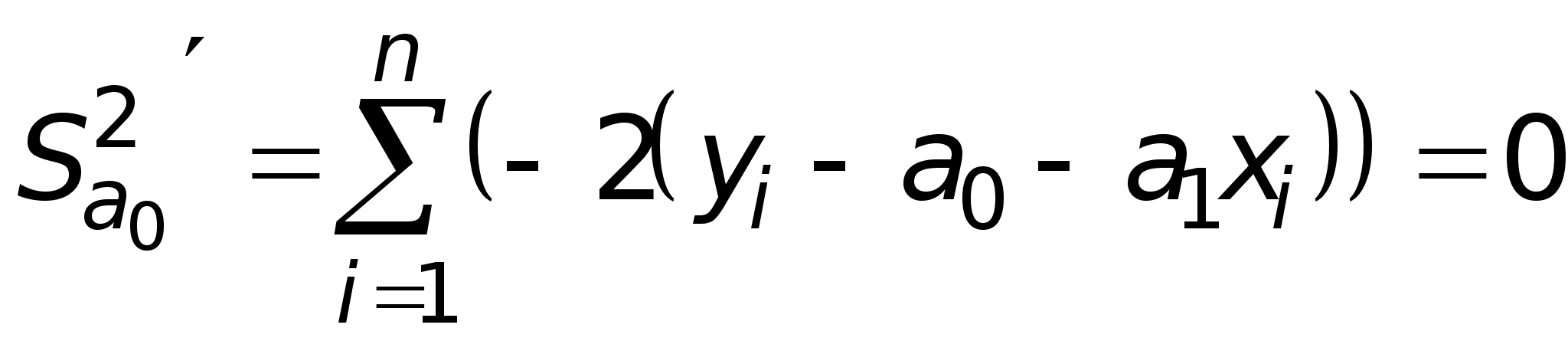 , (2)
, (2)
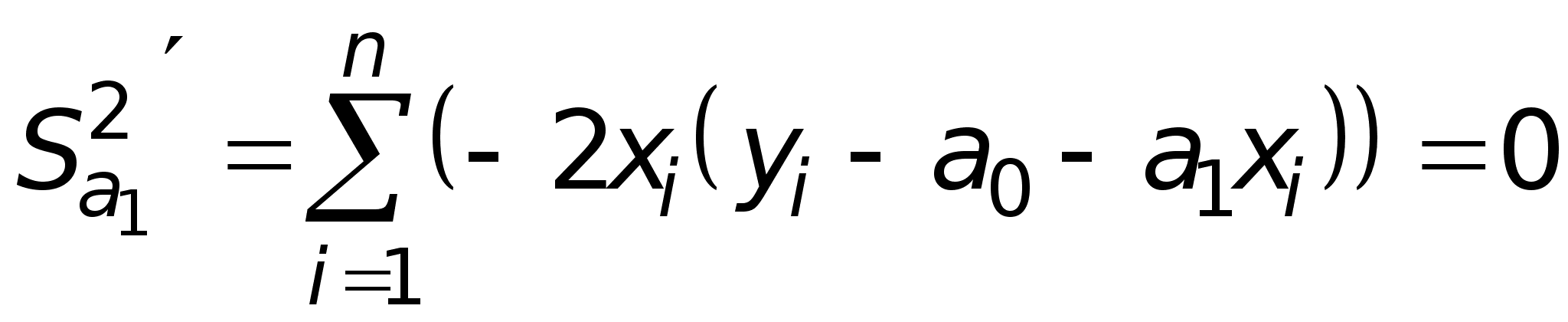 . (3)
. (3)
На самом деле для фунуции S2 = S2(a0,a1) достаточно легко проверить выполнение достаточных условия экстремума, тогда не нужно обращаться к графику функции. Проверку выполнения достаточных условий предоставляем читателю сделать самому.
Уравнения (2) и (3) можно преобразовать:
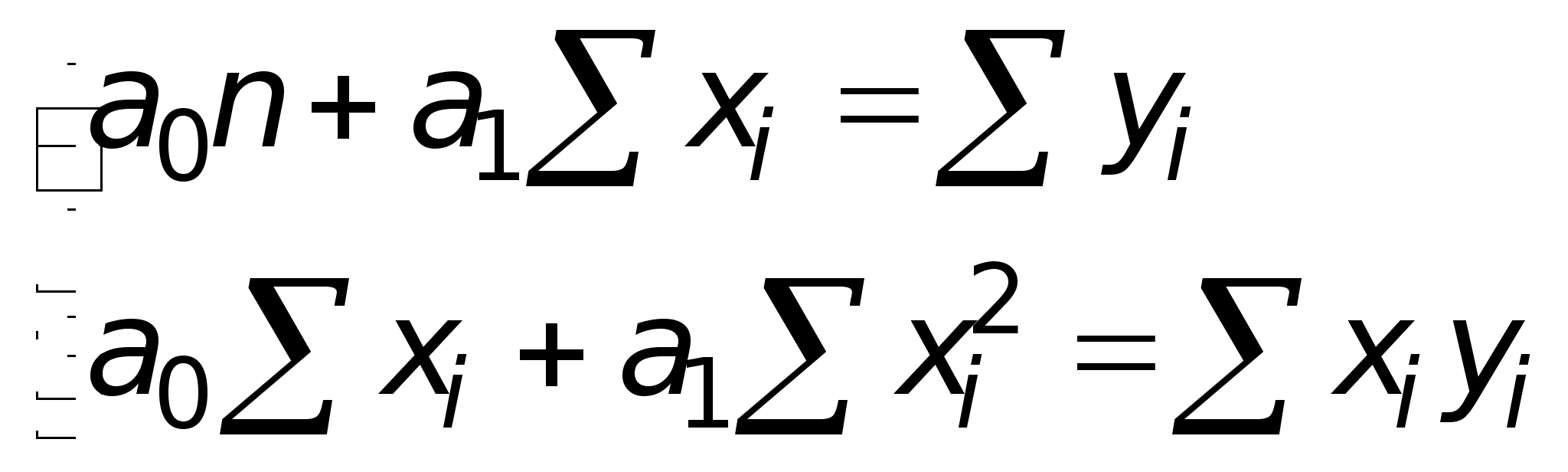 . (4)
. (4)
Получилась так называемая система нормальных уравнений относительно неизвестных величин a0 и a1.
Формула (1) с параметрами a0, a1 определенными из системы (4), называется уравнением регрессии. Прямая линия, описываемая этим уравнением, называется линией регрессии. Для временных рядов обычно вместо слова “регрессия” употребляется слово тренд.
Если
экспериментальные
точки в плоскости
![]() группируются
вдоль некоторой
кривой линии,
то можно подобрать
вместо формулы
(1) другую подходящую
формулу, например,
y = a0 + a1x + a2x2
или y = a0 exp(a1x)
с параметрами
соответственно
a0, a1, a2
и a0, a1,
подставить
ее в выражение
группируются
вдоль некоторой
кривой линии,
то можно подобрать
вместо формулы
(1) другую подходящую
формулу, например,
y = a0 + a1x + a2x2
или y = a0 exp(a1x)
с параметрами
соответственно
a0, a1, a2
и a0, a1,
подставить
ее в выражение
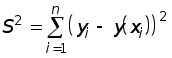 и искать минимум
получившейся
функции S2
при помощи
частных производных
по параметрам.
и искать минимум
получившейся
функции S2
при помощи
частных производных
по параметрам.
Упражнения
1. Найти
частные производные
первого порядка
от следующих
функций:
| 1) |
|
2) |
|
| 3) |
|
4) |
|
| 5) |
|
6) |
|

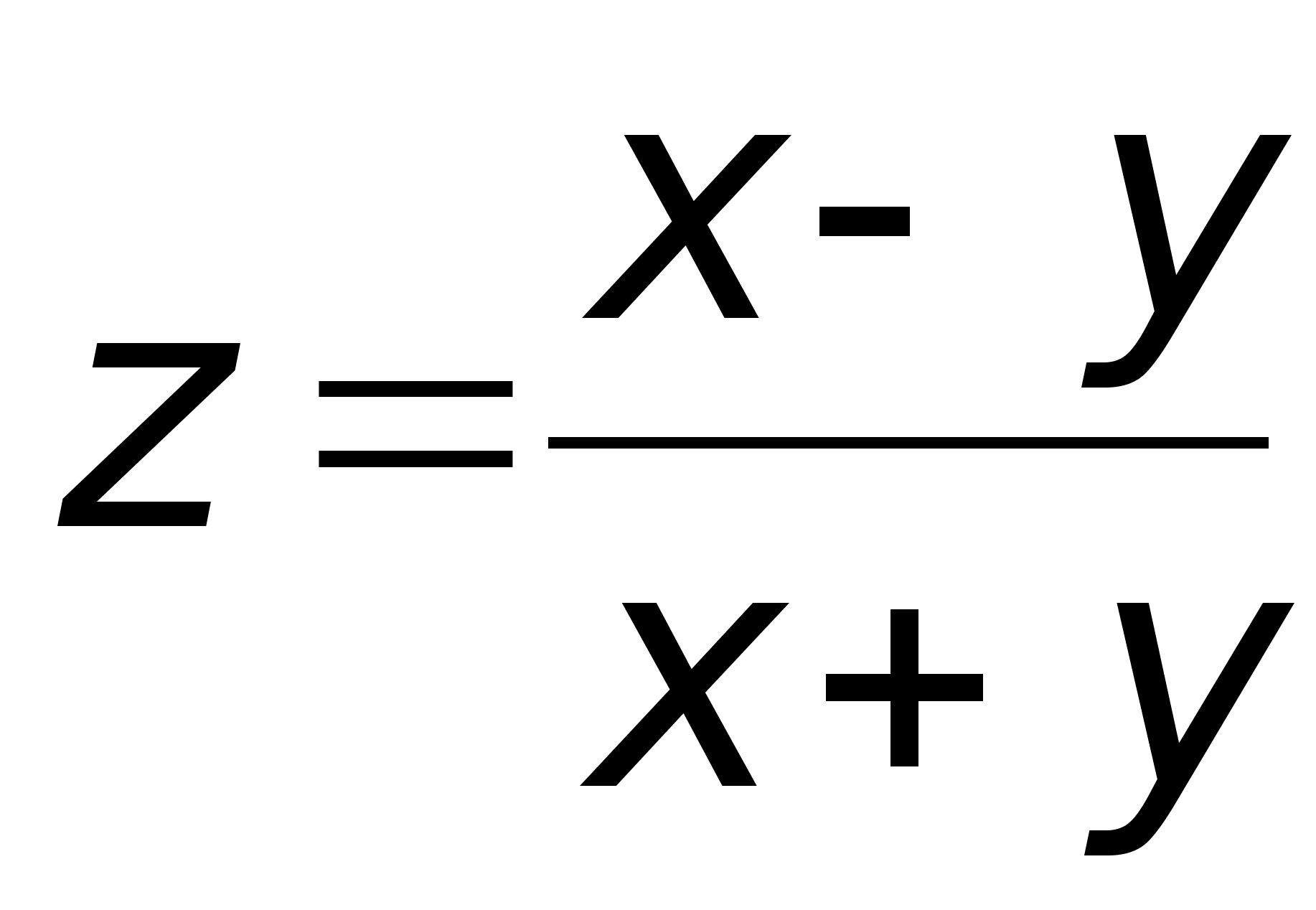 ;
;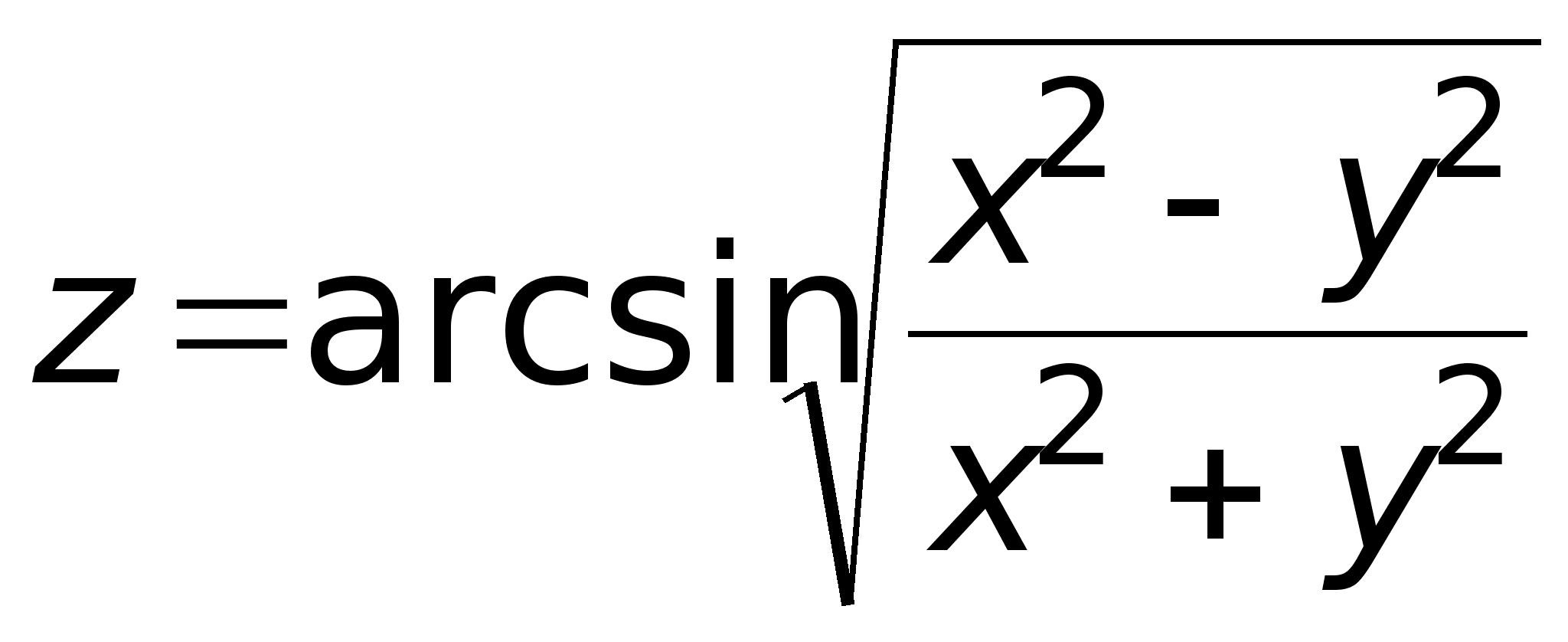 ;
;