
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Решение дифференциального уравнения с последующей аппроксимацией
Реферат: Решение дифференциального уравнения с последующей аппроксимацией
МИНИСТЕРСТВО СВЯЗИ РФ
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ
ХАБАРОВСКИЙ ФИЛИАЛ
К У Р С О В А Я Р А Б О Т А
ПО ИНФОРМАТИКЕ
на тему:
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
С ПОСЛЕДУЮЩЕЙ АППРОКСИМАЦИЕЙ РЕЗУЛЬТАТОВ
Работу выполнила:
студентка I курса
специальности РРТ (ускор.)
Турчина
шифр: 011р-469
2001 г.
С О Д Е Р Ж А Н И Е
Индивидуальное задание - 3
1. Решение дифференциального уравнения методом Эйлера - Коши - 4
1.1. Теоретические сведения - 4
1.2. Ручной расчёт решаемой задачи - 6
2. Аппроксимация. Метод наименьших квадратов - 9
2.1. Теоретические сведения - 9
2.2. Ручной расчёт коэффициентов системы линейных уравнений - 10
3. Решение системы уравнений методом Гаусса - 11
4. Нахождение значений аппроксимирующей функции - 13
5. Расчёт погрешности аппроксимации - 14
6. Построение блок-схемы и разработка программы аппроксимации - 16
Литература - 21
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
1. Решить дифференциальное уравнение y = x + cos ( y / Ö0.3 ) с начальными условиями x0 = 0.7 y0 = 2.1 на интервале [ 0.7 ; 1.7 ] с шагом h = 0.1.
2. Оценить погрешность вычислений при решении дифференциального уравнения методом Эйлера - Коши.
3. Аппроксимировать полученное в п.1. решение параболой методом наименьших квадратов.
4. Рассчитать погрешность аппроксимации.
5. Построить графики решения дифференциального уравнения, аппроксимирующей функции и погрешности аппроксимации.
6. Составить блок-схемы алгоритмов и программы для решения дифференциального уравнения, вычисления коэффициентов аппроксимирующей параболы, расчёта погрешности аппроксимации на языке QBASIC. На печать выдать :
- значения функции y( xi ), являющейся решением дифференциального уравнения в точках xi, найденные с шагом h и с шагом h/2 ;
- значения аппроксимирующей функции F( xi ) в точках xi ;
-
значение погрешности аппроксимации ![]() i = F( xi ) - yi.
i = F( xi ) - yi.
- величину средне - квадратичного отклонения.
1. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
МЕТОДОМ ЭЙЛЕРА - КОШИ
1.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В соответствии с постановкой задачи нужно найти решение дифференциального уравнения первого порядка, т.е. найти такие решения y(x), которые превратили бы дифференциальное уравнение в тождество. Но так как таких решений множество, заданы начальные условия - значения функции y(x) в точке x0, т.е. y(x0) = y0, а так же интервал [ x0 - xn ].
Рис. 1. показывает, что с помощью начальных условий из множества решений можно выбрать одно.
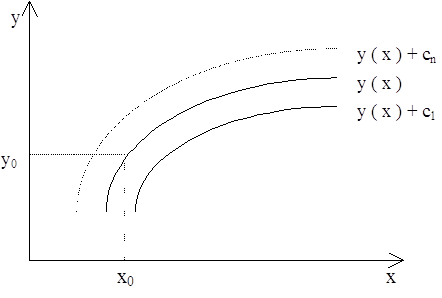
Рис 1. Множество решений дифференциального уравнения.
Метод Эйлера - Коши - наиболее точный метод решения дифференциального уравнения (второй порядок точности). Этот метод предполагает следующий порядок вычислений:
yi+1* = yi + h f( xi ; yi ), где i = 0,1,2 ... n
yi+1 = yi + h (f( xi ; yi ) + f( xi+1 ; yi+1*)) / 2
Число значений n можно найти, разделив интервал на шаг:
n = (xn - xo) / h
Геометрически это означает, что определяется направление касательной к интегральной кривой в исходной точке хi,yi и во вспомогательной точке хi+1,yi+1*, а в качестве окончательного направления берется среднее этих направлений (показано пунктирной линией на рис. 2)

Рис.2. Графическая интерпретация метода Эйлера - Коши.
Решение yi+1, найденное методом Эйлера - Коши, намного ближе к точному решению, чем решение yi+1*, найденное методом Эйлера. Погрешность метода пропорциональна шагу h во второй степени, т.е. метод Эйлера - Коши имеет второй порядок точности.
1.2. РУЧНОЙ РАСЧЁТ РЕШАЕМОЙ ЗАДАЧИ
По условию задачи нужно решить дифференциальное уравнение y = x + cos ( y / Ö0.3 ) с начальными условиями x0 = 0.7, y0 = 2.1 на интервале [ 0.7 ; 1.7 ] с шагом h = 0.1 .
По формуле метода Эйлера -Коши
yi+1* = yi + h f( xi ; yi ),
yi+1 = yi + h (f( xi ; yi ) + f( xi+1 ; yi+1*)) / 2
Найдем y1* и y1
f( x0 ; y0 ) = 0.7 + cos (2.1 / Ö0.3 ) = - 0.069675
x1 = x0 + h = 0.7 + 0.1=0.8
y1* = y0 + h * f( x0 ; y0 ) = 2.1 + 0.1 * (- 0.069675) = 2.093032
y1 = y0 + h * (f( x0 ; y0 ) + f( x0 + h ; y1* )) / 2 = 2.1 + 0.1 * ((- 0.069675) + 0.022266)/2 =
= 2.09763
Аналогично найдём остальные значения x и y :
f( x1 ; y1 ) = 0.8 + cos (2.09763/ Ö0.3 ) = 0.02757
x2 = 0.8 + 0.1 = 0.9
y2* = 2.09763 + 0.1 * 0.02757 = 2.100387
y2 = 2.09763 + 0.1 * (0.02757 + 0.130776) / 2 = 2.105547
f( x2 ; y2 ) = 0.9 + cos (2.105547 / Ö0.3 ) = 0.136831
x3 = 0.9 + 0.1 = 1
y3* = 2.105547 + 0.1 * 0.136831 = 2.11923
y3 = 2.105547 + 0.1 * (0.136831 + 0.25321) / 2 = 2.125049
f( x3 ; y3 ) = 1 + cos (2.125049 / Ö0.3 ) = 0.260317
x4 = 1+ 0.1 = 1.1
y4* = 2.125049 + 0.1 * 0.260317 = 2.1510807
y4 = 2.125049 + 0.1 * (0.260317 + 0.393124) / 2 = 2.157721
f( x4 ; y4 ) = 1.1 + cos (2.157721 / Ö0.3 ) = 0.401751
x5 = 1.1 + 0.1 = 1.2
y5* = 2.157721+ 0.1 * 0.401751 = 2.1978961
y5 = 2.157721 + 0.1 * (0.401751 + 0.556089) / 2 = 2.205613
f( x5 ; y5 ) = 1.2 + cos (2.205613 / Ö1.3 ) = 0.566933
x6 = 1.2 + 0.1 = 1.3
y6* = 2.205613 + 0.1 * 0.566933 = 2.2623063
y6 = 2.205613 + 0.1 * (0.566933 + 0.750302) / 2 = 2.271475
f( x6 ; y6 ) = 1.3 + cos (2.271475 / Ö0.3 ) = 0.764362
x7 = 1.3 + 0.1 = 1.4
y7* = 2.271475 + 0.1 * 0.764362 = 2.347911
y7 = 2.271475 + 0.1 * (0.764362 + 0.987033) / 2 = 2.359045
f( x7 ; y7 ) = 1.4 + cos (2.359045/ Ö0.3 ) = 1.005629
x8 = 1.4 + 0.1 = 1.5
y8* = 2.359045 + 0.1 * 1.005629 = 2.4596079
y8 = 2.359045 + 0.1 * (1.005629 + 1.280033) / 2 = 2.473328
f( x8 ; y8 ) = 1.5 + cos (2.473328 / Ö0.3 ) = 1.304536
x9 = 1.5+ 0.1 = 1.6
y9* = 2.473328 + 0.1 * 1.304536 = 2.6037816
y9 = 2.473328 + 0.1 * (1.304536 + 1.6414317) / 2 = 2.620626
f( x9 ; y9 ) = 1.6 + cos (2.620626 / Ö0.3 ) = 1.6721351
x10 = 1.6 + 0.1 = 1.7
y10* = 2.620626 + 0.1 * 1.6721351 = 2.7878395
y10 = 2.620626 + 0.1 * (1.6721351 + 2.068584) / 2 = 2.807662
Для оценки погрешности вычислений найдём решение дифференциального уравнения с шагом h / 2 до третьей точки:
f( x0 ; y0 ) = 0.7 + cos (2.1 / Ö0.3 ) = - 0.069675
x1 = 0.7 + 0.05 = 0.75
y1* = 2.1 + 0.05 * (- 0.069675) = 2.096516
y1 = 2.1 + 0.05 * ((- 0.069675) + ( - 0.02372)) / 2 = 2.097665
f( x1 ; y1 ) = 0.75 + cos (2.097665 / Ö0.3 ) = - 0.022389
x2 = 0.75 + 0.05 = 0.8
y2* = 2.097665 + 0.05 * (- 0.022389) = 2.096546
y2 = 2.097665 + 0.05 * ((- 0.022389) + 0.026314) / 2 = 2.097763
f( x2 ; y2) = 0.8 + cos (2.097763 / Ö0.3 ) = 0.027724
x3 = 0.8 + 0.05 = 0.85
y3* = 2.097763 + 0.05 * 0.027724 = 2.0991492
y3 = 2.097763 + 0.05 * (0.027724 + 0.079334) / 2 = 2.10044
f( x3 ; y3) = 0.85 + cos (2.10044 / Ö0.3 ) = 0.080838
x4 = 0.85 + 0.05 = 0.9
y4* = 2.10044 + 0.05 * 0.080838 = 2.1044819
y4 = 2.10044 + 0.05 * (0.080838 + 0.135575) / 2 = 2.10585
f( x4; y4) = 0.9 + cos (2.10585 / Ö0.3 ) = 0.137188
x5 = 0.9 + 0.05 = 0.95
y5* = 2.10585 + 0.05 * 0.137188 = 2.1127094
y5 = 2.10585 + 0.05 * (0.137188 + 0.195345) / 2 = 2.114164
f( x5; y5) = 0.95 + cos (2.114164 / Ö0.3 ) = 0.19709
x6 = 0.95 + 0.05 = 1
y6* = 2.114164 + 0.05 * 0.19709 = 2.1240185
y6 = 2.114164 + 0.05 * (0.19709 + 0.259053) / 2 = 2.125567
Для оценки погрешности вычислений используется правило Рунге:
yi+1 = yih + (yih/2 - yih ) / (2p - 1) , где:
р - порядок метода, для Эйлера - Коши р = 2
Рассчитаем погрешность вычисления в точке х = 1. Найдем уточненное решение:
y(1) = 2.125049 + (2.125567 - 2.125049) / (22 - 1) = 2.1252216
e ih = 2p (yih - yih/2) / (2p - 1) = 22 (2.125567 - 2.125049) / 3 = 6.9 * 10 -4
e ih/2 = (yih - yih/2) / (2p - 1) = (2.125567 - 2.125049) / 3 = 1.73 * 10 -4
Таблица 1. Значения X и Y, полученные с помощью ручного расчёта.
| I | X ( I ) | Y ( I ) |
| 0 | 0.7 | 2.1 |
| 1 | 0.8 | 2.09763 |
| 2 | 0.9 | 2.105547 |
| 3 | 1 | 2.125049 |
| 4 | 1.1 | 2.157721 |
| 5 | 1.2 | 2.205613 |
| 6 | 1.3 | 2.271475 |
| 7 | 1.4 | 2.359045 |
| 8 | 1.5 | 2.473328 |
| 9 | 1.6 | 2.620626 |
| 10 | 1.7 | 2.807662 |
График решения дифференциального уравнения представлен на рисунке 3.
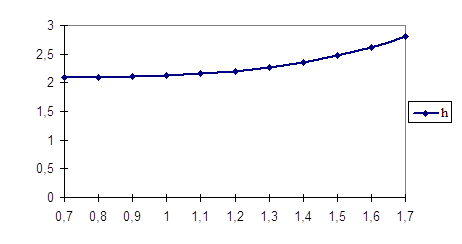
2. АППРОКСИМАЦИЯ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
2.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Исходя из постановки задачи, нужно аппроксимировать полученное в п.1. решение ( Таблица 1. ) параболой методом наименьших квадратов, т.е. нужно найти функцию, в данном случае параболу, которая в точках X ( I ) принимала бы значения, как можно более близкие к значениям Y ( I ). Парабола является функцией с тремя параметрами: F (x) = ax2 + bx + c
Сумма квадратов разностей значений функции и решений дифференциального уравнения (Таблица 1.) должна быть минимальной, т.е.:
![]() ( ax2 + bx + c - yi
)2 => min
( ax2 + bx + c - yi
)2 => min
Функция будет иметь минимум, когда все частные производные равны нулю.
DF / da = 0, dF / db = 0, dF / dc = 0
После преобразований получим систему уравнений:
a11a + a12b + a13c = b1
a21a + a22b + a23c = b2
a31a + a32b + a33c = b3
где a11 = ![]() , a12 = a21 =
, a12 = a21 = ![]() , a13 = a22 =
a31 =
, a13 = a22 =
a31 = ![]() , a23 = a32
=
, a23 = a32
=![]() xi , a33 = n +
1
xi , a33 = n +
1
b1 = ![]() yi , b2 =
yi , b2 =![]() xi yi , b3 =
xi yi , b3 =![]() yi .
yi .
2.2. РУЧНОЙ РАСЧЁТ КОЭФФИЦИЕНТОВ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Рассчитаем коэффициенты системы трёх линейных уравнений по формулам, взятым из п.2.2.:
а11 = 0.74 + 0.84 + 0.94 + 1.04 + 1.14 + 1.24 + 1.34 + 1.44 + 1.54 + 1.64 + 1.74 = 32.5094
а12 = а21 = 0.73 + 0.83 + 0.93 + 1.03 + 1.13 + 1.23 + 1.33 + 1.43 + 1.53 + 1.63 + 1.73 = 22.9680
а13 = а22 = а31 = 0.72 + 0.82 + 0.92 + 1.02 + 1.12 + 1.22 + 1.32 +1.42+1.52+1.62+1.72 = 16.9400
а23 = а32 = 0.7 + 0.8 + 0.9 + 1 + 1.1 + 1.2 + 1.3 + 1.4 + 1.5 + 1.6 + 1.7 = 13.2000
а33 = n + 1 = 11
b1 = 2.1 * 0.72 + 2.09763 * 0.82 + 2.105547 * 0.92 + 2.125049 * 1.02 + 2.157721 * 1.12 + 2.205613 * 1.22 + 2.271475 * 1.32 + 2.359045 * 1.42 + 2.473328 * 1.52 + 2.620626 * 1.62 + 2.807662 * 1.72 = 40.83941
b2 = 2.1 * 0.7 + 2.09763 * 0.8 + 2.105547 * 0.9 + 2.125049 * 1.0 + 2.157721 * 1.1 + 2.205613 * 1.2 + 2.271475 * 1.3 + 2.359045 * 1.4 + 2.473328 * 1.5 + 2.620626 * 1.6 + 2.807662 * 1.7 = 31.119972
b3 = 2.1 + 2.09763 + 2.105547 + 2.125049 + 2.157721 + 2.205613 + 2.271475 + 2.359045 + 2.473328 + 2.620626 + 2.807662 = 25.3237
Получим систему уравнений:
32.5094a + 22.968b + 16.94c = 40.83941
22.968a + 16.94b + 13.2c = 31.119972
16.94a + 13.2b + 11c = 25.3237
Теперь нужно решить эту систему методом Гаусса и найти коэффициенты a,b,c.
3. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ ГАУССА
Суть этого метода состоит в том, что систему линейных уравнений преобразуют к системе с треугольной матрицей, а потом решают уравнения, начиная с последнего.
Решим систему уравнений, полученную в п. 2.2.:
Первое уравнение считается основным, его мы не изменяем. Второе уравнение нужно преобразовать так, чтобы первый его коэффициент стал равен нулю. Для этого второе уравнение нужно умножить на такой множитель, чтобы первые коэффициенты первого и второго уравнения стали равны.
Найдём множитель:
μ21 = а21 / а11 = 22.968 / 32.5094 = 0.7065
Умножим на него первое уравнение:
32.5094a * 0.7065 + 22.968b * 0.7065 + 16.94 * 0.7065 = 40.83941 * 0.7065
Получим:
22.968a + 16.2269b + 11.9681c = 28.853043
Теперь нужно это уравнение почленно вычесть из второго:
0a + 0.7131b + 1.2319c = 2.266929
Аналогично преобразуем третье уравнение:
i31 = a31 / a11 = 16.94 / 32.5094 = 0.5211
32.5094a * 0.5211 + 22.968b * 0.5211 + 16.94c * 0.5211 = 40.83941 * 0.5211
16.94a + 11.9686b + 8.8274c = 21.281416
Вычтем это уравнение из третьего, получим:
0a +1.2314b + 2.1726c = 4.042284
Таким образом, получится система, эквивалентная исходной:
32.5094a + 22.968b + 16.94c = 40.83941
0.7131b + 1.2319c = 2.266929
1.2314b + 2.1726c = 4.042284
Третье уравнение нужно преобразовать так, чтобы второй его коэффициент стал равен нулю. Найдём множитель:
μ32 = a32 / a22 = 1.2314 / 0.7131 = 1.7268
Умножим второе уравнение на него:
0.7131b * 1.7268 + 1.2319c * 1.7268 = 2.266929 * 1.7268
1.2314b + 2.1272c = 3.914533
Вычтем получившееся уравнение из третьего:
0b + 0.0454c = 0.127751
Получим треугольную матрицу, эквивалентную исходной:
32.5094a + 22.968b + 16.94c = 40.83941
0.7131b + 1.2319c = 2.266929
0.0454c = 0.127751
Теперь найдём коэффициенты:
c = 0.127751 / 0.0454 = 2.813899
b = (2.266929 - 1.2319 * 2.813899) / 0.7131 = - 1.682111
a = (40.83941 - 16.94 * 2.813899 - 22.968 * (- 1.682111) ) / 32.5094 = 0.978384
Проверим результаты вычислений, подставив полученные значения корней в исходную систему:
32.5094 * 0.978384 + 22.968 * (- 1.682111) + 16.94 * 2.813899 = 40.83941
22.968 * 0.978384 + 16.94 * (- 1.682111) + 13.2 * 2.813899 = 31.119972
16.94 * 0.978384 + 13.2 * (- 1.682111) + 11 * 2.813899 = 25.3237
40.8394 » 40.83941
31.12 » 31.119972
25.3228 » 25.3237
Таким образом, уравнение аппроксимирующей параболы имеет вид:
F (x) = 0.978384x2 - 1.682111x + 2.813899
4. НАХОЖДЕНИЕ ЗНАЧЕНИЙ АППРОКСИМИРУЮЩЕЙ ФУНКЦИИ
Найдём значения функции F(x) = 0.978384 x2 - 1.682111 x + 2.813899
на интервале [0.7; 1.7] с шагом h=0.1
x0 = 0.7
F( x0 ) = 0.978384 * 0.72 - 1.682111 * 0.7 + 2.813899 = 2.118622
x1 = x0 + h = 0.7 + 0.1 = 0.8
F( x1 ) = 0.978384 * 0.82 - 1.682111 * 0.8 + 2.813899 = 2.095734
x2 = 0.8 + 0.1 = 0.9
F( x2 ) = 0.978384 * 0.92 - 1.682111 * 0.9 + 2.813899 = 2.092711
x3 = 0.9 + 0.1 = 1.0
F( x3 ) = 0.978384 * 1.02 - 1.682111 * 1.0 + 2.813899 = 2.109553
x4 = 1.0 + 0.1 = 1.1
F( x4 ) = 0.978384 * 1.12 - 1.682111 * 1.1 + 2.813899 = 2.14626
x5 = 1.1 + 0.1 = 1.2
F( x5 ) = 0.978384 * 1.22 - 1.682111 * 1.2 + 2.813899 = 2.202831
x6 = 1.2 + 0.1 = 1.3
F( x6 ) = 0.978384 * 1.32 -1.682111 * 1.3 + 2.813899 = 2.279266
x7 = 1.3 + 0.1 = 1.4
F( x7 ) = 0.978384 * 1.42 - 1.682111 * 1.4 + 2.813899 = 2.375567
x8 = 1.4 + 0.1 = 1.5
F( x8 ) = 0.978384 * 1.52 - 1.682111 * 1.5 + 2.813899 = 2.491732
x9 = 1.5 + 0.1 = 1.6
F( x9 ) = 0.978384 * 1.62 - 1.682111 * 1.6 + 2.813899 = 2.627762
x10 = 1.6 + 0.1 = 1.7
F( x10 ) = 0.978384 * 1.72 - 1.682111 * 1.7 + 2.813899= 2.783656
5. РАСЧЕТ ПОГРЕШНОСТИ АПРОКСИМАЦИИ.
Для вычисления погрешности аппроксимации вычислим величину среднеквадратичного отклонения:
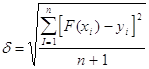
Здесь yi - значения решения дифференциального уравнения, полученные в п.1.2. (см. Таблицу 1), F(xi) - значения аппроксимирующей функции при тех же значениях xi, полученные в п. 4. Их разность показывает величину отклонения аппроксимирующей функции от аппроксимируемой в узлах xi.
Рассчитаем погрешность аппроксимации:
![]() 0 = F( x0 ) - y0 = 2.118622 - 2.1 = 0.018622
0 = F( x0 ) - y0 = 2.118622 - 2.1 = 0.018622
![]() 02
= 3.46779 * 10 - 4
02
= 3.46779 * 10 - 4
![]() 1 = F( x1 ) - y1 = 2.095734 - 2.09763 = - 0.001896
1 = F( x1 ) - y1 = 2.095734 - 2.09763 = - 0.001896
![]() 12
= 3.59482 *10 - 6
12
= 3.59482 *10 - 6
![]() 2 = F( x2 ) - y2 = 2.092711 - 2.105547 = - 0.012836
2 = F( x2 ) - y2 = 2.092711 - 2.105547 = - 0.012836
![]() 22
= 1.64763 * 10 - 4
22
= 1.64763 * 10 - 4
![]() 3 = F( x3 ) - y3 = 2.109553 - 2.125049 = - 0.015496
3 = F( x3 ) - y3 = 2.109553 - 2.125049 = - 0.015496
![]() 32
= 2.40126 * 10 - 4
32
= 2.40126 * 10 - 4
![]() 4 = F( x4 ) - y4 = 2.14626 - 2.157721 = - 0.011461
4 = F( x4 ) - y4 = 2.14626 - 2.157721 = - 0.011461
![]() 42
= 1.31355 * 10 - 4
42
= 1.31355 * 10 - 4
![]() 5 = F( x5 ) - y5 = 2.202831 - 2.205613 = - 0.002782
5 = F( x5 ) - y5 = 2.202831 - 2.205613 = - 0.002782
![]() 52
= 7.73953 * 10 - 6
52
= 7.73953 * 10 - 6
![]() 6 = F( x6 ) - y6 = 2.279266 - 2.271475 = 0.007791
6 = F( x6 ) - y6 = 2.279266 - 2.271475 = 0.007791
![]() 62
= 6.06997 * 10 - 5
62
= 6.06997 * 10 - 5
![]() 7 = F( x7 ) - y7 = 2.375567 - 2.359045 = 0.06522
7 = F( x7 ) - y7 = 2.375567 - 2.359045 = 0.06522
![]() 72
= 2.72977 * 10 - 4
72
= 2.72977 * 10 - 4
![]() 8 = F( x8 ) - y8 = 2.491732 - 2.473328 = 0.08404
8 = F( x8 ) - y8 = 2.491732 - 2.473328 = 0.08404
![]() 82
= 3.38707 * 10 - 4
82
= 3.38707 * 10 - 4
![]() 9 = F( x9 ) - y9 = 2.627762 - 2.620626 = 0.007136
9 = F( x9 ) - y9 = 2.627762 - 2.620626 = 0.007136
![]() 92
= 5.09225 * 10 - 5
92
= 5.09225 * 10 - 5
![]() 10 = F( x10 ) - y10 = 2.783656 - 2.807662 = - 0.024006
10 = F( x10 ) - y10 = 2.783656 - 2.807662 = - 0.024006
![]() 102
= 5.76288 * 10 -4
102
= 5.76288 * 10 -4
![]()
![]()
|
Данные расчётов снесены в Таблицу 2.
Таблица 2. Расчёт погрешности аппроксимации.
| I |
xi |
yi |
F(xi) |
|
|
| 0 | 0.7 | 2.1 | 2.118622 | 0.018622 |
3.46779 * 10 - 4 |
| 1 | 0.8 | 2.09763 | 2.095734 | - 0.001896 |
3.59482 * 10 - 6 |
| 2 | 0.9 | 2.105547 | 2.092711 | - 0.012836 |
1.64763 * 10 - 4 |
| 3 | 1.0 | 2.125049 | 2.109553 | - 0.015496 |
2.40126 * 10 - 4 |
| 4 | 1.1 | 2.157721 | 2.14626 | - 0.011461 |
1.31355 * 10 - 4 |
| 5 | 1.2 | 2.205613 | 2.202831 | - 0.002782 |
7.73953 * 10 - 6 |
| 6 | 1.3 | 2.271475 | 2.279266 | 0.007791 |
6.06997 * 10 - 5 |
| 7 | 1.4 | 2.359045 | 2.375567 | 0.06522 |
2.72977 * 10 - 4 |
| 8 | 1.5 | 2.473328 | 2.491732 | 0.08404 |
3.38707 * 10 - 4 |
| 9 | 1.6 | 2.620626 | 2.627762 | 0.007136 |
5.09225 * 10 - 5 |
| 10 | 1.7 | 2.807662 | 2.783656 | - 0.024006 |
5.76288 * 10 - 4 |
График погрешности аппроксимации представлен на рисунке 4.
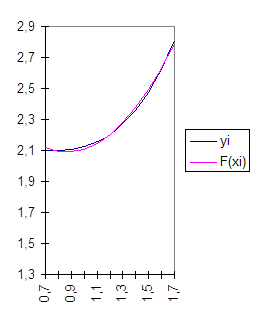
График аппроксимирующей
функции представлен на рисунке 5.
6. ПОСТРОЕНИЕ БЛОК-СХЕМЫ И РАЗРАБОТКА ПРОГРАММЫ АППРОКСИМАЦИИ
Блок-схема алгоритма решения задачи аппроксимации методом наименьших квадратов представлена на Рис. 6.
Первым шагом осуществляется ввод значений X(I),Y(I),N.
Далее обнуляются значения всех коэффициентов. В цикле рассчитываются коэффициенты 3-х линейных уравнений. (см. п. 2.2). После цикла приравниваем одинаковые коэффициенты в матрице. Потом выполняется подпрограмма решения линейных уравнений.
Следующим шагом происходит описание функции пользователя:
FNY(X) = K(1) X 2 + K(2) X + K(3)
Следующий цикл находит значения аппроксимирующей функции, разность между этими значениями и корнями дифференциального уравнения Y(I), квадрат разности, а также производит их суммирование. Далее находится величина погрешности аппроксимации и все данные выводятся на экран.
Общая программа решения дифференциального уравнения с последующей аппроксимацией результатов представлена на рис. 7 вместе с программой решения дифференциального уравнения, так как из нее получают значения X(I) и Y(I).
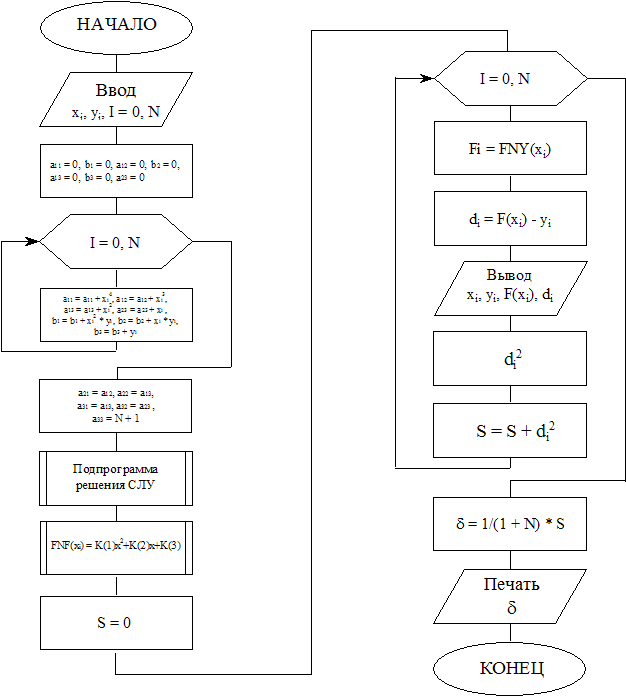
Рис. 6. Блок-схема алгоритма решения задачи аппроксимации методом наименьших квадратов.
CLS
PRINT " Нахождение коэффициентов по методу Эйлера - Коши"
X0 = 0.7
XN = 1.7
Y0 = 2.1
H = 0.1
N = (XN - X0) / H
DIM X(N)
DIM Y(N)
X(0) = X0
Y(0) = Y0
FOR I = 0 TO N - 1
X(I + 1) = X(I) + H
Y(I + 1)* = Y(I) + H * (X(I) + COS(Y(I) / SQR(0.3)))
Y(I +1) = Y(I)+H*((X(I)+COS(Y(I)/SQR(0.3)))+(X(I+1)+COS(Y(I+1)* / SQR(0.3))))/2
PRINT " X("; I; ")="; X(I), , "Y("; I; ")="; Y(I)
NEXT I
I = 10: PRINT " X("; I; ")="; X(I), "Y("; I; ")="; Y(I)
PRINT "Нахождение коэффициентов по методу наименьших квадратов"
PRINT "и погрешности аппроксимации"
a11 = 0: b1 = 0: a12 = 0: b2 = 0: a13 = 0: b3 = 0: a23 = 0: a33 = N + 1
FOR I = 0 TO N
a11 = a11 + X(I) ^ 4
a12 = a12 + X(I) ^ 3
a13 = a13 + X(I) ^ 2
a23 = a23 + X(I)
b1 = b1 + (X(I) ^ 2) * Y(I)
b2 = b2 + X(I) * Y(I)
b3 = b3 + Y(I)
NEXT I
a21 = a12: a22 = a13: a31 = a13: a32 = a23: S = 0
REM Начало подпрограммы решения СЛУ методом Гаусса
DIM К(3)
m21 = a21 / a11
m31 = a31 / a11
a22 = a22 - a12 * m21
a23 = a23 - a13 * m21
b2 = b2 - b1 * m21
a32 = a32 - a12 * m31
a33 = a33 - a13 * m31
b3 = b3 - b1 * m31
m32 = a32 / a22
a33 = a33 - a23 * m32
b3 = b3 - b2 * m32
К(3) = b3 / a33
К(2) = (b2 - К(3) * a23) / a22
К(1) = (b1 - К(3) * a13 - К(2) * a12) / a11
REM Конец подпрограммы решения СЛУ методом Гаусса
DIM F(N)
DEF FNY(X) = K(1) * X ^ 2 + K(2) * X + K(3)
PRINT "-----------------------------------------------------------------------------------"
PRINT " X(I) | y(I) | F(x(I)) | F(x(I))-y(I) | d^2 "
PRINT "-----------------------------------------------------------------------------------"
FOR I = 0 TO N
F(I) = FNY(X(I))
D = F(I) - Y(I)
S = S + D ^ 2
PRINT X(I), Y(I), f(I), D, D^2
NEXT I
E = SQR(S / (N + 1))
PRINT "Погрешность ="; E
END
ЛИТЕРАТУРА
1. Витенберг И.М. Программирование на языке БЕЙСИК. Москва. «Радио и связь».1991.
2. Гери М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. Пер. с англ. – Москва. «МИР» 1982.
3. Горбунова Н.Г. Методические указания к лабораторным работам по курсу Информатика, ч.2 «Численные методы» - Хабаровск, 1996.
4. Спесивцев А.В. Руководство пользователя по языку Бейсик. Москва. «Радио и связь». 1992. «ВЕСТА».
5. Методические указания для оформления пояснительных записок курсовых и дипломных проектов - Хабаровск, 1997.
