
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Применение алгоритма RSA для шифрования потоков данных
Реферат: Применение алгоритма RSA для шифрования потоков данных
СОДЕРЖАНИЕ
| Введение | 5 |
|
1.Постановка задачи |
10 |
| 2. Алгоритм RSA | 11 |
| 2.1. Система шифрования RSA | 12 |
| 2.2.Сложность теоретико-числовых алгоритмов | 16 |
| 2.2.1. Алгоритм вычисления | 17 |
| 2.2.2. Алгоритм Евклида | 18 |
| 2.2.3. Алгоритм решения уравнения | 18 |
| 2.2.4. Алгоритм нахождения делителей многочлена в кольце | 21 |
| 3. Качественная теория алгоритма RSA | 23 |
| 3.1. Алгоритм, доказывающий непростоту числа | 24 |
| 3.2. Нахождение больших простых чисел | 26 |
| 3.3. Проверка большого числа на простоту | 30 |
| 4. Практическая реализация алгоритма | 37 |
| 4.1. Реализованные алгоритмы | 37 |
| 4.2. Анализ результатов | 38 |
| 5. Выводы | 39 |
| 5.1 Алгоритм | 39 |
| 5.2 Алгоритм и программа | 39 |
| Заключение | 41 |
| Список использованных источников | 42 |
| Приложение 1. Листинг программы | 43 |
| Приложение 2. Главная форма программы | 46 |
|
Приложение 3. Форма базы данных абонентов |
47 |
|
Приложение 4. Форма нахождения простых чисел и генерации ключей |
48 |
ВВЕДЕНИЕ
Проблема защиты информации путем ее преобразования, исключающего ее прочтение посторонним лицом, волновала человеческий ум с давних времен. История криптографии - ровесница истории человеческого языка. Более того, первоначально письменность сама по себе была своеобразной криптографической системой, так как в древних обществах ею владели только избранные. Священные книги древнего Египта, древней Индии тому примеры.
История криптографии условно можно разделить на 4 этапа.
1) наивная криптография.
2) формальная криптография.
3) научная криптография.
4) компьютерная криптография.
Для наивной криптографии (до нач. XVI века) характерно использование любых (обычно примитивных) способов запутывания противника относительно содержания шифруемых текстов. На начальном этапе для защиты информации использовались методы кодирования и стеганографии, которые родственны, но не тождественны криптографии.
Большинство из используемых шифров сводились к перестановке или моноалфавитной подстановке. Одним из первых зафиксированных примеров является шифр Цезаря, состоящий в замене каждой буквы исходного текста на другую, отстоящую от нее в алфавите на определенное число позиций. Другой шифр, полибианский квадрат, авторство которого приписывается греческому писателю Полибию, является общей моноалфавитной подстановкой, которая проводится с помощью случайно заполненной алфавитом квадратной таблицейдля греческого алфавита размер составляет 5x5). Каждая буква исходного текста заменяется на букву, стоящую в квадрате снизу от нее.
Этап формальной криптографии (кон. XV века - нач. XX века) связан с появлением формализованных и относительно стойких к ручному криптоанализу шифров. В европейских странах это произошло в эпоху Возрождения, когда развитие науки и торговли вызвало спрос на надежные способы защиты информации. Важная роль на этом этапе принадлежит Леону Батисте Альберти, итальянскому архитектору, который одним из первых предложил многоалфавитную подстановку. Данный шифр, получивший имя дипломата XVI века Блеза Вижинера, состоял в последовательном «сложении» букв исходного текста с ключом (процедуру можно облегчить с помощью специальной таблицы). Его работа «Трактат о шифре» (1466) считается первой научной работой по криптологии.
Одной из первых печатных работ, в которой обобщены и сформулированы известные на тот момент алгоритмы шифрования является труд «Полиграфия» (1508 г.) немецкого аббата Иоганна Трисемуса. Ему принадлежат два небольших, но важных открытия: способ заполнения полибианского квадрата (первые позиции заполняются с помощью легко запоминаемого ключевого слова, остальные - оставшимися буквами алфавита) и шифрование пар букв (биграмм).
Простым но стойким способом многоалфавитной замены (подстановки биграмм) является шифр Плейфера, который был открыт в начале XIX века Чарльзом Уитстоном. Уитстону принадлежит и важное усовершенствование - шифрование «двойным квадратом». Шифры Плейфера и Уитстона использовались вплоть до первой мировой войны, так как с трудом поддавались ручному криптоанализу.
В XIX веке голландец Керкхофф сформулировал главное требование к криптографическим системам, которое остается актуальным и поныне: секретность шифров должна быть основана на секретности ключа, но не алгоритма.
Наконец, последним словом в донаучной криптографии, которое обеспечили еще более высокую криптостойкосить, а также позволило автоматизировать (в смысле механизировать) процесс шифрования стали роторные криптосистемы.
Одной из первых подобных систем стала изобретенная в 1790 году Томасом Джефферсоном, будущим президентом США механическая машина. Многоалфавитная подстановка с помощью роторной машины реализуется вариацией взаимного положения вращающихся роторов, каждый из которых осуществляет «прошитую» в нем подстановку.
Практическое распространение роторные машины получили только в начале XX века. Одной из первых практически используемых машин, стала немецкая Enigma, разработанная в 1917 году Эдвардом Хеберном и усовершенствованная Артуром Кирхом. Роторные машины активно использовались во время второй мировой войны. Помимо немецкой машины Enigma использовались также устройства Sigaba (США), Турех (Великобритания), Red, Orange и Purple2 (Япония). Роторные системы -вершина формальной криптографии так как относительно просто реализовывали очень стойкие шифры. Успешные криптоатаки на роторные системы стали возможны только с появлением ЭВМ в начале 40-х годов.
Главная отличительная черта научной криптографии (30-е - 60-е годы XX века) - появление криптосистем со строгим математическим обоснованием криптостойкости. К началу 30-х годов окончательно сформировались разделы математики, являющиеся научной основой криптологии: теория вероятностей и математическая статистика, общая алгебра, теория чисел, начали активно развиваться теория алгоритмов, теория информации, кибернетика. Своеобразным водоразделом стала работа Клода Шеннона «Теория связи в секретных системах» (1949), где сформулированы теоретические принципы криптографической защиты информации. Шеннон ввел понятия «рассеивание» и «перемешивание», обосновал возможность создания сколь угодно стойких криптосистем.
В 60-х годах ведущие криптографические школы подошли к созданию блочных шифров, еще более стойких по сравнению с роторными криптосистемами, однако допускающие практическую реализацию только в виде цифровых электронных устройств.
Компьютерная криптография (с 70-х годов XX века) обязана своим появлением вычислительным средствам с производительностью, достаточной для реализации критосистем, обеспечивающих при большой скорости шифрования на несколько порядков более высокую криптостойкость, чем «ручные» и «механические» шифры.
Первым классом криптосистем, практическое применение которых стало возможно с появлением мощных и компактных вычислительных средств, стали блочные шифры. В 70-е годы был разработан американский стандарт шифрования DES (принят в 1978 году). Один из его авторов, Хорст Фейстел (сотрудник IBM), описал модель блочных шифров, на основе которой были построены другие, более стойкие симметричные криптосистемы, в том числе отечественный стандарт шифрования ГОСТ 28147-89.
С появлением DES обогатился и криптоанализ, для атак на американский алгоритм был создано несколько новых видов криптоанализа (линейный, дифференциальный и т.д.), практическая реализация которых опять же была возможна только с появлением мощных вычислительных систем.
В середине 70-х годов произошел настоящий прорыв в современной криптографии - появление асимметричных криптосистем, которые не требовали передачи секретного ключа между сторонами. Здесь отправной точкой принято считать работу, опубликованную Уитфилдом Диффи и Мартином Хеллманом в 1976 году под названием «Новые направления в современной криптографии». В ней впервые сформулированы принципы обмена шифрованной информацией без обмена секретным ключом. Независимо к идее асимметричных криптосистем подошел Ральф Меркли. Несколькими годами позже Рон Ривест, Ади Шамир и Леонард Адлеман открыли систему RSA, первую практическую асимметричную криптосистему, стойкость которой была основана на проблеме факторизации больших простых чисел. Асимметричная криптография открыла сразу несколько новых прикладных направлений, в частности системы электронной цифровой подписи (ЭЦП) и электронных денег.
В 80-90-е годы появились совершенно новые направления криптографии: вероятностное шифрование, квантовая криптография и другие. Осознание их практической ценности еще впереди. Актуальной остается и задача совершенствования симметричных криптосистем. В 80-90-х годах были разработаны нефейстеловские шифры (SAFER, RC6 и др.), а в 2000 году после открытого международного конкурса был принят новый национальный стандарт шифрования США - AES.
1. ПОСТАНОВКА ЗАДАЧИ
Безопасность передачи данных по каналам связи является актуальной. Современные компьютерные сети не исключение. К сожалению, в сетевых операционных системах (Windows NT/XP, Novell и т.д.) иностранного производства, как следствие, из-за экспортных соображений уровень алгоритмов шифрования заметно снижен.
Задача: исследовать современные методы шифрования и их приложимость к шифрованию потоков данных. Разработать собственную библиотеку алгоритмов шифрования и программный продукт, демонстрирующий работу этих алгоритмов при передаче данных в сети.
2. АЛГОРИТМ RSA
Труды Евклида и Диофанта, Ферма и Эйлера, Гаусса, Чебышева и Эрмита содержат остроумные и весьма эффективные алгоритмы решения диофантовых уравнений, выяснения разрешимости сравнений, построения больших по тем временам простых чисел, нахождения наилучших приближений и т.д. В последние два десятилетия, благодаря в первую очередь запросам криптографии и широкому распространению ЭВМ, исследования по алгоритмическим вопросам теории чисел переживают период бурного и весьма плодотворного развития.
Вычислительные машины и электронные средства связи проникли практически во все сферы человеческой деятельности. Немыслима без них и современная криптография. Шифрование и дешифрование текстов можно представлять себе как процессы переработки целых чисел при помощи ЭВМ, а способы, которыми выполняются эти операции, как некоторые функции, определённые на множестве целых чисел. Всё это делает естественным появление в криптографии методов теории чисел. Кроме того, стойкость ряда современных криптосистем обосновывается только сложностью некоторых теоретико-числовых задач.
Но возможности
ЭВМ имеют
определённые
границы. Приходится
разбивать
длинную цифровую
последовательность
на блоки ограниченной
длины и шифровать
каждый такой
блок отдельно.
Мы будем считать
в дальнейшем,
что все шифруемые
целые числа
неотрицательны
и по величине
меньше некоторого
заданного
(скажем, техническими
ограничениями)
числа m.
Таким же условиям
будут удовлетворять
и числа, получаемые
в процессе
шифрования.
Это позволяет
считать и те,
и другие числа
элементами
кольца вычетов
![]() .
Шифрующая
функция при
этом может
рассматриваться
как взаимнооднозначное
отображение
колец вычетов
.
Шифрующая
функция при
этом может
рассматриваться
как взаимнооднозначное
отображение
колец вычетов
![]()
а число
![]() представляет
собой сообщение
представляет
собой сообщение
![]() в зашифрованном
виде.
в зашифрованном
виде.
Простейший
шифр такого
рода - шифр замены,
соответствует
отображению
![]() при некотором
фиксированном
целом k.
Подобный шифр
использовал
еще Юлий Цезарь.
Конечно, не
каждое отображение
при некотором
фиксированном
целом k.
Подобный шифр
использовал
еще Юлий Цезарь.
Конечно, не
каждое отображение
![]() подходит для
целей надежного
сокрытия информации.
подходит для
целей надежного
сокрытия информации.
В 1978 г. американцы
Р. Ривест, А. Шамир
и Л. Адлеман
(R.L.Rivest.
A.Shamir.
L.Adleman)
предложили
пример функции
![]() ,
обладающей
рядом замечательных
достоинств.
На её основе
была построена
реально используемая
система шифрования,
получившая
название по
первым буквам
имен авторов
-система RSA.
Эта функция
такова, что
,
обладающей
рядом замечательных
достоинств.
На её основе
была построена
реально используемая
система шифрования,
получившая
название по
первым буквам
имен авторов
-система RSA.
Эта функция
такова, что
1) существует
достаточно
быстрый алгоритм
вычисления
значений
![]() ;
;
2) существует
достаточно
быстрый алгоритм
вычисления
значений обратной
функции
![]() ;
;
3) функция
![]() обладает некоторым
«секретом»,
знание которого
позволяет
быстро вычислять
значения
обладает некоторым
«секретом»,
знание которого
позволяет
быстро вычислять
значения
![]() ;
в противном
же случае вычисление
;
в противном
же случае вычисление
![]() становится
трудно разрешимой
в вычислительном
отношении
задачей, требующей
для своего
решения столь
много времени,
что по его
становится
трудно разрешимой
в вычислительном
отношении
задачей, требующей
для своего
решения столь
много времени,
что по его
прошествии
зашифрованная
информация
перестает
представлять
интерес для
лиц, использующих
отображение
![]() в качестве
шифра.
в качестве
шифра.
Еще до выхода из печати статьи копия доклада в Массачусетском Технологическом институте, посвящённого системе RSA. была послана известному популяризатору математики М. Гарднеру, который в 1977 г. в журнале Scientific American опубликовал статью посвящённую этой системе шифрования. В русском переводе заглавие статьи Гарднера звучит так: Новый вид шифра, на расшифровку которого потребуются миллионы лет. Именно эта статья сыграла важнейшую роль в распространении информации об RSA, привлекла к криптографии внимание широких кругов неспециалистов и фактически способствовала бурному прогрессу этой области, произошедшему в последовавшие 20 лет.
2.1. система шифрования RSA
Пусть
![]() и
и
![]() натуральные
числа. Функция
натуральные
числа. Функция
![]() реализующая
схему RSA,
устроена следующим
образом
реализующая
схему RSA,
устроена следующим
образом
![]() .
(1)
.
(1)
Для расшифровки
сообщения
![]() достаточно
решить сравнение
достаточно
решить сравнение
![]() .
(2)
.
(2)
При некоторых
условиях на
![]() и
и
![]() это сравнение
имеет единственное
решение
это сравнение
имеет единственное
решение
![]() .
.
Для того,
чтобы описать
эти условия
и объяснить,
как можно найти
решение, нам
потребуется
одна теоретико-числовая
функция, так
называемая
функция Эйлера.
Эта функция
натурального
аргумента
![]() обозначается
обозначается
![]() и равняется
количеству
целых чисел
на отрезке от
1 до
и равняется
количеству
целых чисел
на отрезке от
1 до
![]() ,
взаимно простых
с
,
взаимно простых
с
![]() .
Так
.
Так
![]() и
и
![]() для любого
простого числа
для любого
простого числа
![]() и натурального
и натурального
![]() .
Кроме того,
.
Кроме того,
![]() для любых
натуральных
взаимно простых
для любых
натуральных
взаимно простых
![]() и
и
![]() .
Эти свойства
позволяют легко
вычислить
значение
.
Эти свойства
позволяют легко
вычислить
значение
![]() ,
если известно
разложение
числа
,
если известно
разложение
числа
![]() на простые
сомножители.
на простые
сомножители.
Если показатель
степени
![]() в сравнении
(2) взаимно прост
с
в сравнении
(2) взаимно прост
с
![]() ,
то сравнение
(2) имеет единственное
решение. Для
того, чтобы
найти его, определим
целое число
,
то сравнение
(2) имеет единственное
решение. Для
того, чтобы
найти его, определим
целое число
![]() ,
удовлетворяющее
условиям
,
удовлетворяющее
условиям
![]() .
(3)
.
(3)
Такое число
существует,
поскольку
![]() ,
и притом единственно.
Здесь и далее
символом
,
и притом единственно.
Здесь и далее
символом
![]() будет обозначаться
наибольший
общий делитель
чисел
будет обозначаться
наибольший
общий делитель
чисел
![]() и
и
![]() .
Классическая
теорема Эйлера,
утверждает,
что для каждого
числа
.
Классическая
теорема Эйлера,
утверждает,
что для каждого
числа
![]() ,
взаимно простого
с
,
взаимно простого
с
![]() ,
выполняется
сравнение
,
выполняется
сравнение
![]() и, следовательно.
и, следовательно.
![]() .
(4)
.
(4)
Таким
образом, в
предположении
![]() ,
единственное
решение сравнения
(2) может быть
найдено в виде
,
единственное
решение сравнения
(2) может быть
найдено в виде
![]() .
(5)
.
(5)
Если дополнительно
предположить,
что число
![]() состоит из
различных
простых сомножителей,
то сравнение
(5) будет выполняться
и без предположения
состоит из
различных
простых сомножителей,
то сравнение
(5) будет выполняться
и без предположения
![]() .
Действительно,
обозначим
.
Действительно,
обозначим
![]() и
и
![]() .
Тогда
.
Тогда
![]() делится на
делится на
![]() ,
а из (2) следует,
что
,
а из (2) следует,
что
![]() .
Подобно (4), теперь
легко находим
.
Подобно (4), теперь
легко находим
![]() .
А кроме того,
имеем
.
А кроме того,
имеем
![]() .
Получившиеся
сравнения в
силу
.
Получившиеся
сравнения в
силу
![]() дают нам (5).
дают нам (5).
Функция
(1), принятая в
системе RSA,
может быть
вычислена
достаточно
быстро. Обратная
к
![]() функция
функция
![]() вычисляется
по тем же правилам,
что и
вычисляется
по тем же правилам,
что и
![]() ,
лишь с заменой
показателя
степени
,
лишь с заменой
показателя
степени
![]() на
на
![]() .
Таким образом,
для функции
(1) будут выполнены
указанные выше
свойства 1) и
2).
.
Таким образом,
для функции
(1) будут выполнены
указанные выше
свойства 1) и
2).
Для вычисления
функции (1) достаточно
знать лишь
числа
![]() и
и
![]() .
Именно они
составляют
открытый ключ
для шифрования.
А вот для вычисления
обратной функции
требуется знать
число
.
Именно они
составляют
открытый ключ
для шифрования.
А вот для вычисления
обратной функции
требуется знать
число
![]() .
оно и является
«секретом»,
о котором речь
идёт в пункте
в). Казалось
бы. ничего не
стоит. зная
число
.
оно и является
«секретом»,
о котором речь
идёт в пункте
в). Казалось
бы. ничего не
стоит. зная
число
![]() .
разложить его
на простые
сомножители,
вычислить затем
с помощью известных
правил значение
.
разложить его
на простые
сомножители,
вычислить затем
с помощью известных
правил значение
![]() и, наконец, с
помощью (3) определить
нужное число
и, наконец, с
помощью (3) определить
нужное число
![]() .
Все шаги этого
вычисления
могут быть
реализованы
достаточно
быстро, за
исключением
первого. Именно
разложение
числа
.
Все шаги этого
вычисления
могут быть
реализованы
достаточно
быстро, за
исключением
первого. Именно
разложение
числа
![]() на простые
множители и
составляет
наиболее трудоемкую
часть вычислений.
В теории чисел
несмотря на
многолетнюю
её историю и
на очень интенсивные
поиски в течение
последних 20
лет, эффективный
алгоритм разложения
натуральных
чисел на множители
так и не найден.
Конечно, можно,
перебирая все
простые числа
до
на простые
множители и
составляет
наиболее трудоемкую
часть вычислений.
В теории чисел
несмотря на
многолетнюю
её историю и
на очень интенсивные
поиски в течение
последних 20
лет, эффективный
алгоритм разложения
натуральных
чисел на множители
так и не найден.
Конечно, можно,
перебирая все
простые числа
до
![]() ,
и. деля на них
,
и. деля на них
![]() ,
найти требуемое
разложение.
Но, учитывая,
что количество
простых в этом
промежутке,
асимптотически
равно
,
найти требуемое
разложение.
Но, учитывая,
что количество
простых в этом
промежутке,
асимптотически
равно
![]() ,
находим, что
при
,
находим, что
при
![]() ,
записываемом
100 десятичными
цифрами, найдётся
не менее
,
записываемом
100 десятичными
цифрами, найдётся
не менее
![]() простых чисел,
на которые
придётся делить
простых чисел,
на которые
придётся делить
![]() при разложении
его на множители.
Очень грубые
прикидки показывают,
что компьютеру,
выполняющему
миллион делений
в секунду, для
разложения
числа
при разложении
его на множители.
Очень грубые
прикидки показывают,
что компьютеру,
выполняющему
миллион делений
в секунду, для
разложения
числа
![]() таким способом
на простые
сомножители
потребуется
не менее, чем
таким способом
на простые
сомножители
потребуется
не менее, чем
![]() лет. Известны
и более эффективные
способы разложения
целых чисел
на множители,
чем простой
перебор простых
делителей, но
и они работают
очень медленно.
лет. Известны
и более эффективные
способы разложения
целых чисел
на множители,
чем простой
перебор простых
делителей, но
и они работают
очень медленно.
Авторы
схемы RSA
предложили
выбирать число
![]() в виде произведения
двух простых
множителей
в виде произведения
двух простых
множителей
![]() и
и
![]() ,
примерно одинаковых
по величине.
Так как
,
примерно одинаковых
по величине.
Так как
![]() ,
(6)
,
(6)
то единственное
условие на
выбор показателя
степени
![]() в отображении
(1) есть
в отображении
(1) есть
![]() .
(7)
.
(7)
Итак, лицо,
заинтересованное
в организации
шифрованной
переписки с
помощью схемы
RSA,
выбирает два
достаточно
больших простых
числа
![]() и
и
![]() .
Перемножая
их, оно находит
число
.
Перемножая
их, оно находит
число
![]() .
Затем выбирается
число
.
Затем выбирается
число
![]() ,
удовлетворяющее
условиям (7),
вычисляется
с помощью (6) число
,
удовлетворяющее
условиям (7),
вычисляется
с помощью (6) число
![]() и с помощью (3)
- число
и с помощью (3)
- число
![]() .
Числа
.
Числа
![]() и
и
![]() публикуются,
число
публикуются,
число
![]() остается секретным.
Теперь любой
может отправлять
зашифрованные
с помощью (1)
сообщения
организатору
этой системы,
а организатор
легко сможет
расшифровывать
их с помощью
(5).
остается секретным.
Теперь любой
может отправлять
зашифрованные
с помощью (1)
сообщения
организатору
этой системы,
а организатор
легко сможет
расшифровывать
их с помощью
(5).
Для иллюстрации
своего метода
Ривест, Шамир
и Адлеман
зашифровали
таким способом
некоторую
английскую
фразу. Сначала
она стандартным
образом (а=01, b=02,
.... z=26,
пробел=00) была
записана в виде
целого числа
![]() ,
а затем зашифрована
с помощью отображения
(1) при
,
а затем зашифрована
с помощью отображения
(1) при
m=11438162575788886766932577997614661201021829672124236256256184293570 6935245733897830597123563958705058989075147599290026879543541
и
![]() .
Эти два числа
были опубликованы,
причем дополнительно
сообщалось,
что
.
Эти два числа
были опубликованы,
причем дополнительно
сообщалось,
что
![]() .
где
.
где
![]() и
и
![]() - простые числа,
записываемые
соответственно
64 и 65 десятичными
знаками. Первому,
кто расшифрует
соответствующее
сообщение
- простые числа,
записываемые
соответственно
64 и 65 десятичными
знаками. Первому,
кто расшифрует
соответствующее
сообщение
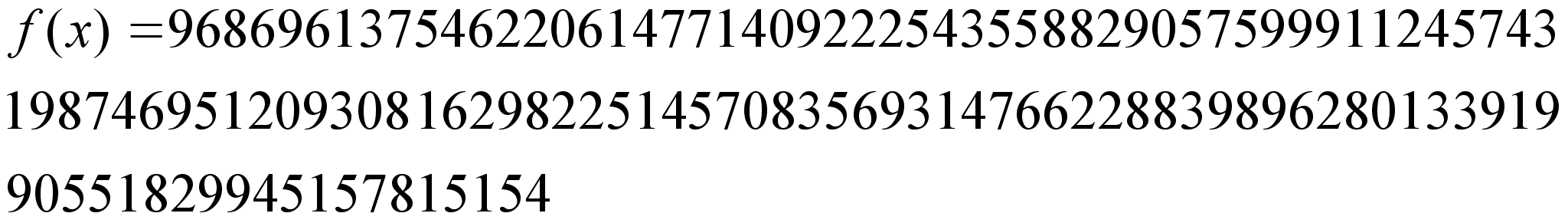 ,
,
была обещана награда в 100$.
Эта история
завершилась
спустя 17 лет в
1994 г., когда D.
Atkins,
M.
Graff,
А. К. Lenstra
и Р. С. Leyland
сообщили о
расшифровке
фразы. Числа
![]() и
и
![]() оказались
равными
оказались
равными
![]() ,
,
![]() .
.
Этот замечательный результат (разложение на множители 129-значного десятичного числа) был достигнут благодаря использованию алгоритма разложения чисел на множители, называемого методом квадратичного решета. Выполнение вычислений потребовало колоссальных ресурсов. В работе, возглавлявшейся четырьмя авторами проекта, и продолжавшейся после предварительной теоретической подготовки примерно 220 дней, на добровольных началах участвовало около 600 человек и примерно 1600 компьютеров, объединённых сетью Internet. Наконец, отметим, что премия в 100$ была передана в Free Software Foundation.
2.2.Сложность теоретико-числовых алгоритмов
Сложность алгоритмов теории чисел обычно принято измерять количеством арифметических операций (сложений, вычитаний, умножений и делений с остатком), необходимых для выполнения всех действий, предписанных алгоритмом. Впрочем, это определение не учитывает величины чисел, участвующих в вычислениях. Ясно, что перемножить два стозначных числа значительно сложнее, чем два однозначных, хотя при этом и в том, и в другом случае выполняется лишь одна арифметическая операция. Поэтому иногда учитывают ещё и величину чисел, сводя дело к так называемым битовым операциям, т. е. оценивая количество необходимых операций с цифрами 0 и 1, в двоичной записи чисел.
Говоря о сложности алгоритмов, мы будем иметь в виду количество арифметических операций. При построении эффективных алгоритмов и обсуждении верхних оценок сложности обычно хватает интуитивных понятий той области математики, которой принадлежит алгоритм. Формализация же этих понятий требуется лишь тогда, когда речь идёт об отсутствии алгоритма или доказательстве нижних опенок сложности.
Приведем теперь примеры достаточно быстрых алгоритмов с опенками их сложности. Здесь и в дальнейшем мы не будем придерживаться формального описания алгоритмов, стараясь в первую очередь объяснить смысл выполняемых действий.
Следующий
алгоритм вычисляет
![]() за
за
![]() арифметических
операций. При
этом, конечно,
предполагается,
что натуральные
числа
арифметических
операций. При
этом, конечно,
предполагается,
что натуральные
числа
![]() и
и
![]() не превосходят
по величине
не превосходят
по величине
![]() .
.
2.2.1.
Алгоритм
вычисления
![]()
Представим
 в двоичной
системе счисления
в двоичной
системе счисления
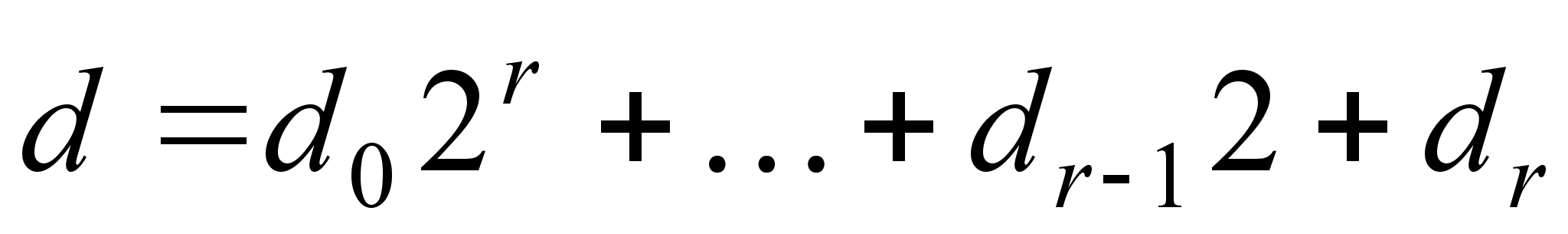 ,
где
,
где
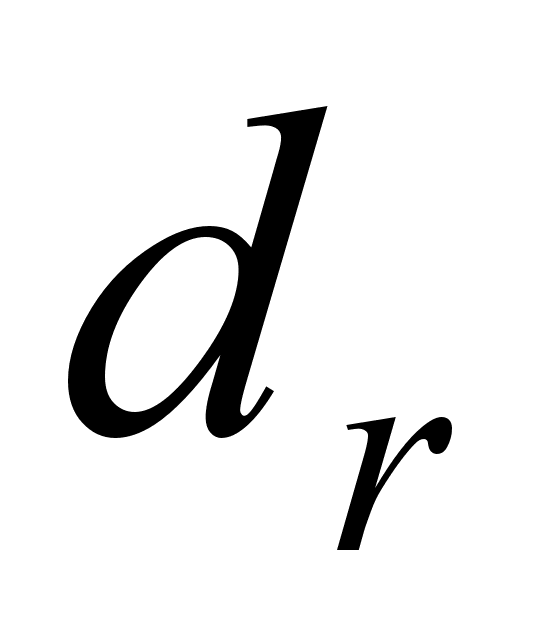 ,
цифры в двоичном
представлении,
равны 0 или 1,
,
цифры в двоичном
представлении,
равны 0 или 1,
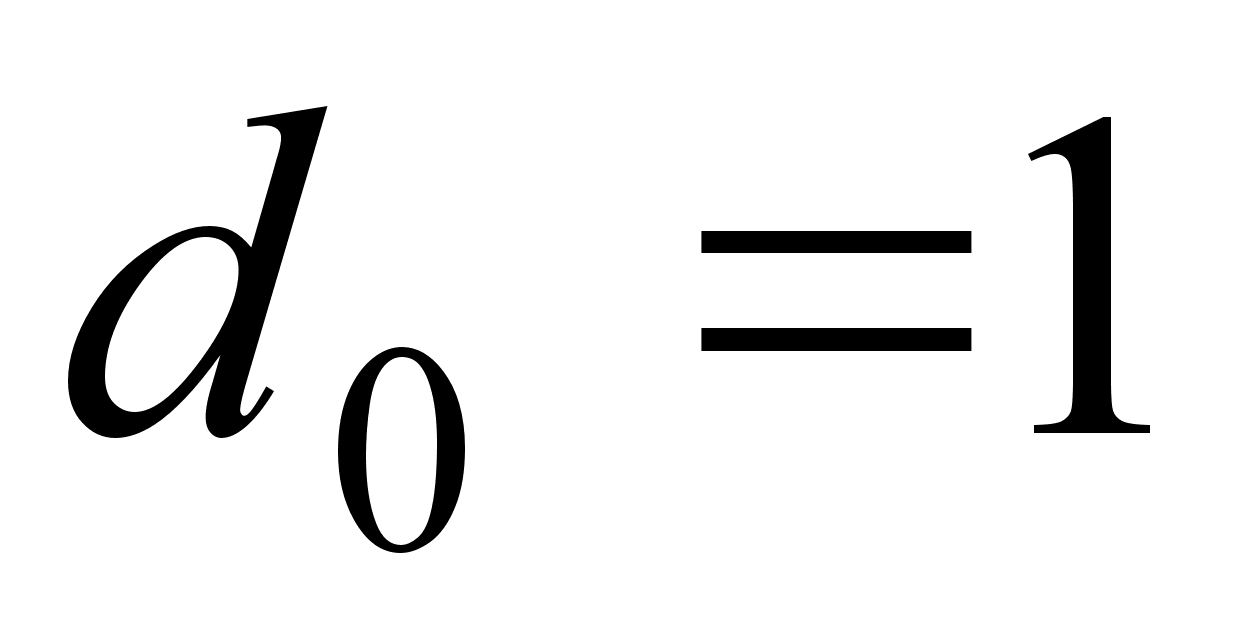 .
.Положим
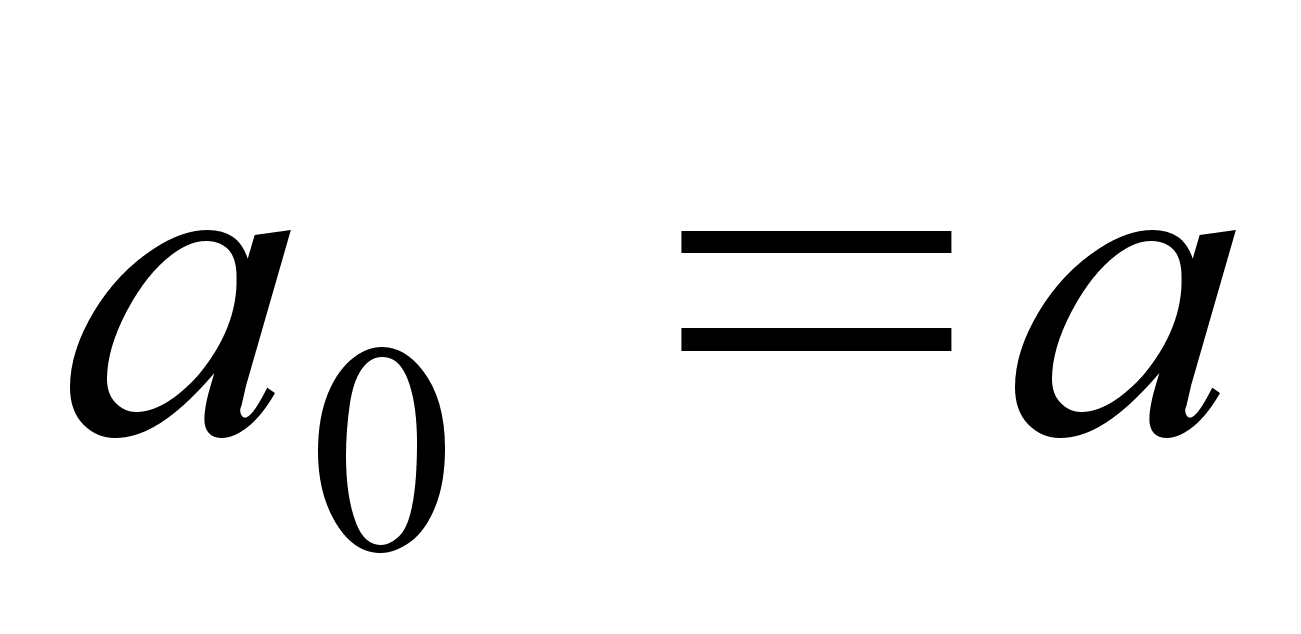 и затем для
и затем для
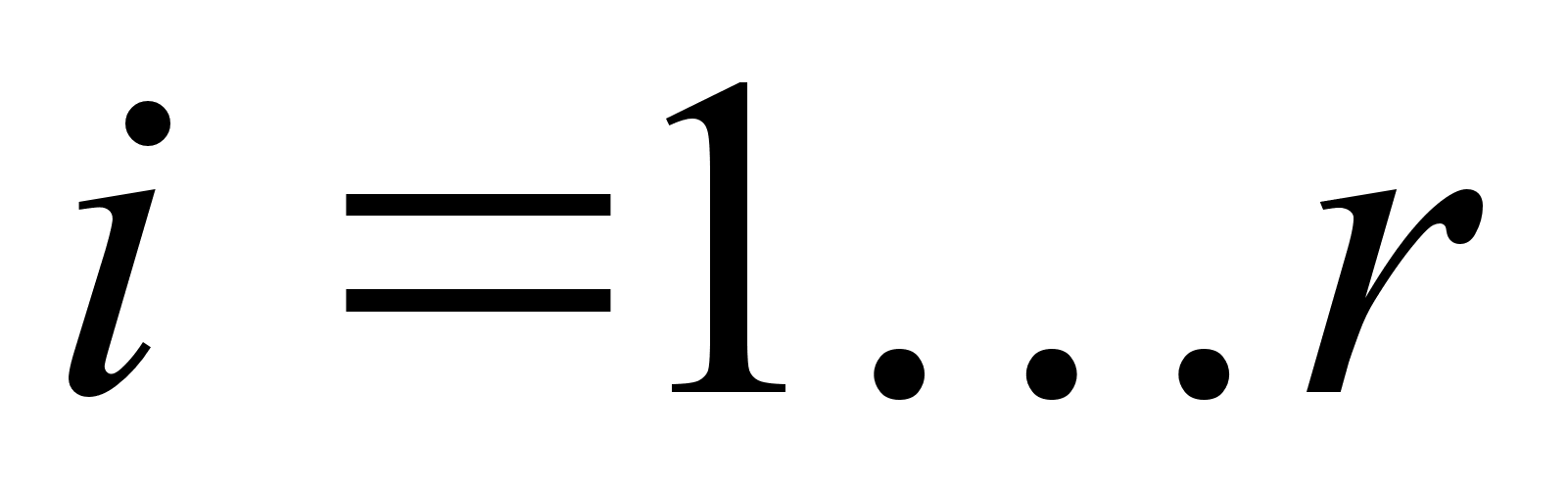 вычислим
вычислим
![]() .
.
3) ![]() есть искомый
вычет
есть искомый
вычет
![]() .
.
Справедливость этого алгоритма вытекает из сравнения
![]() ,
,
легко
доказываемого
индукцией по
![]() .
.
Так как
каждое вычисление
на шаге 2 требует
не более трёх
умножений
по модулю
![]() и этот шаг
выполняется
и этот шаг
выполняется
![]() раз, то сложность
алгоритма может
быть оценена
величиной
раз, то сложность
алгоритма может
быть оценена
величиной
![]() .
.
Второй
алгоритм - это
классический
алгоритм Евклида
вычисления
наибольшего
общего делителя
целых чисел.
Мы предполагаем
заданными два
натуральных
числа
![]() и
и
![]() и вычисляем
их наибольший
общий делитель
и вычисляем
их наибольший
общий делитель
![]() .
.
2.2.2. Алгоритм Евклида
Вычислим
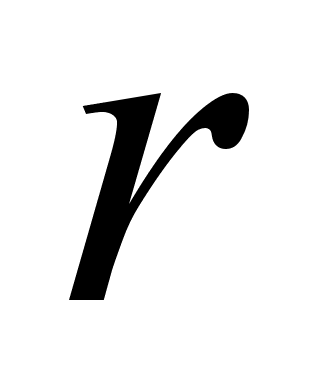 - остаток от
деления числа
- остаток от
деления числа
 на
на
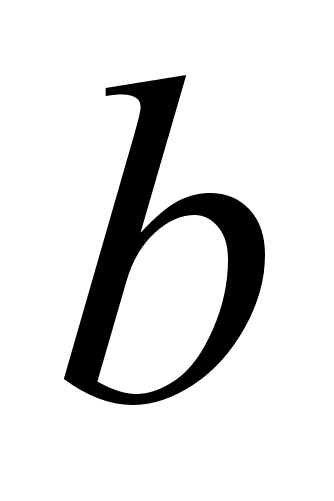 ,
,
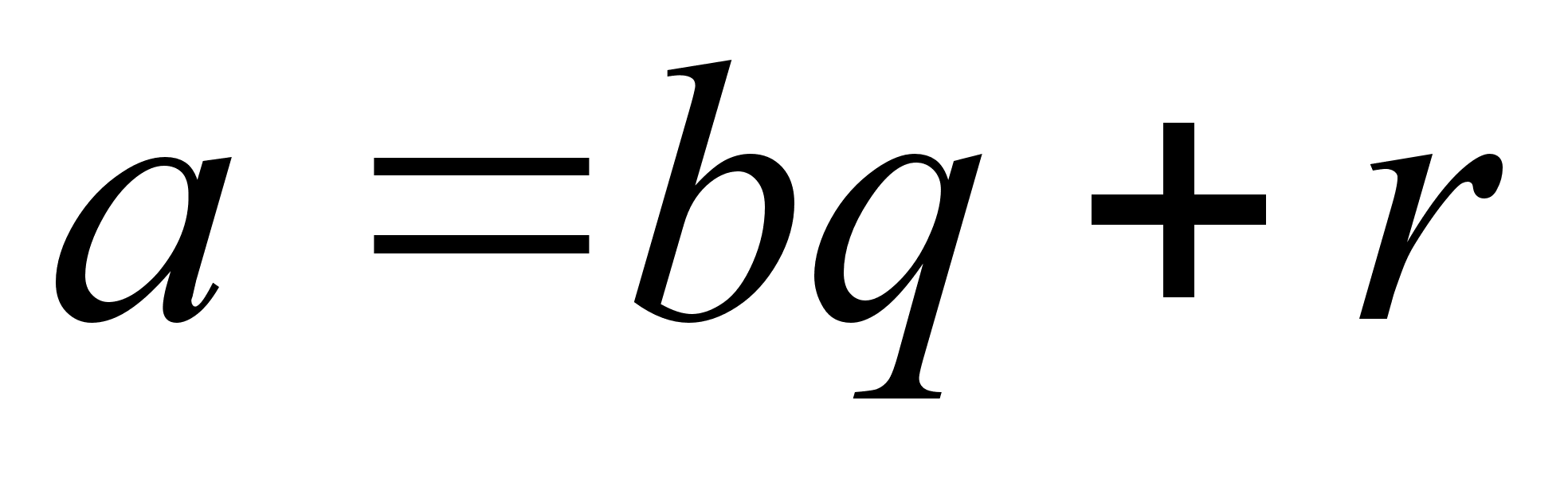 ,
,
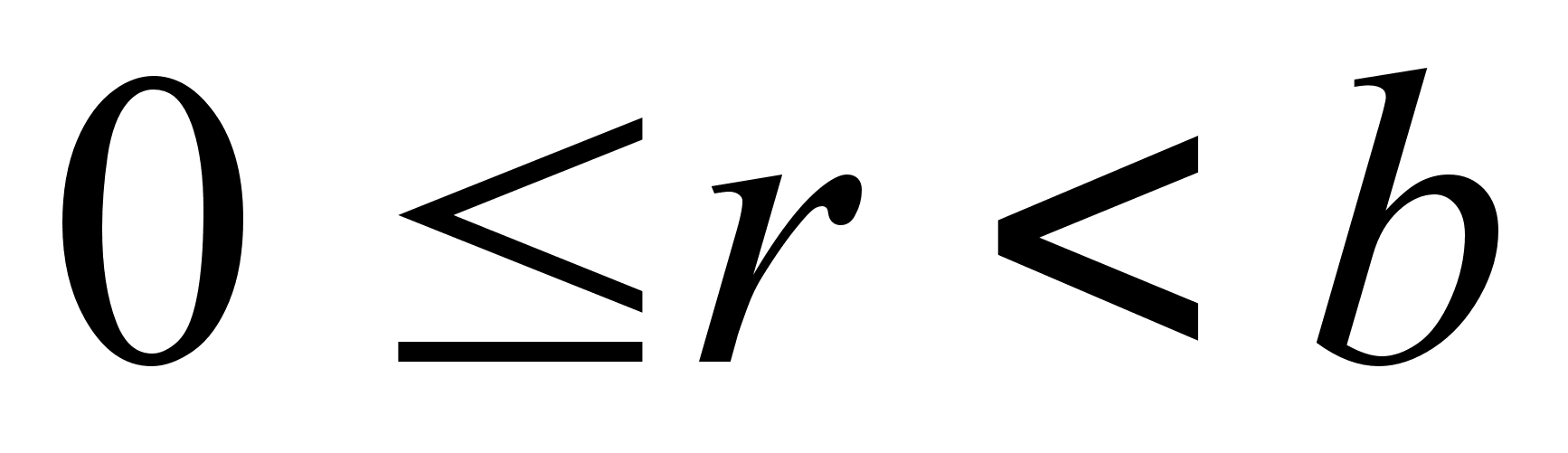 .
.Если
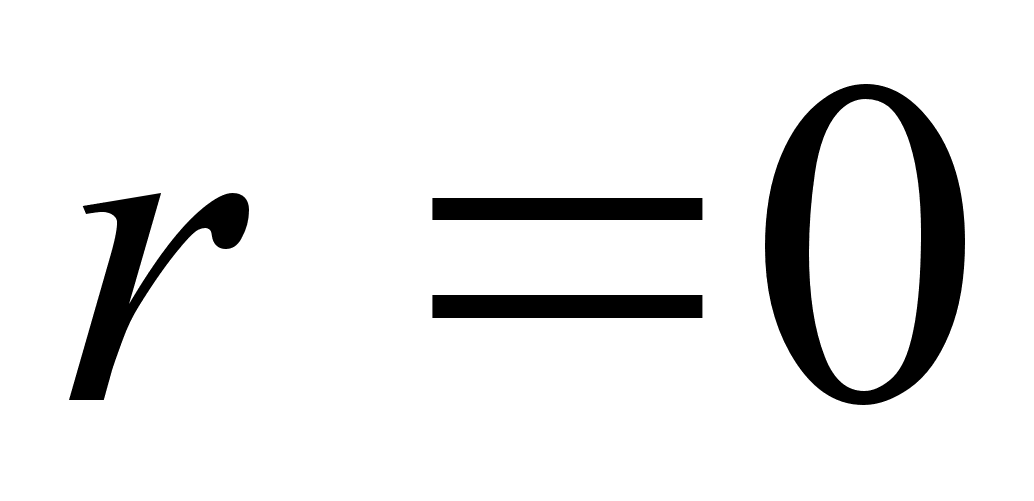 ,
то
,
то
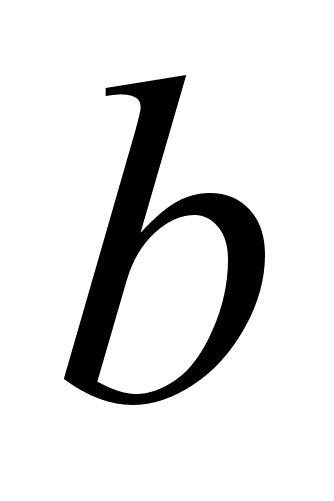 есть искомое
число.
есть искомое
число.Если
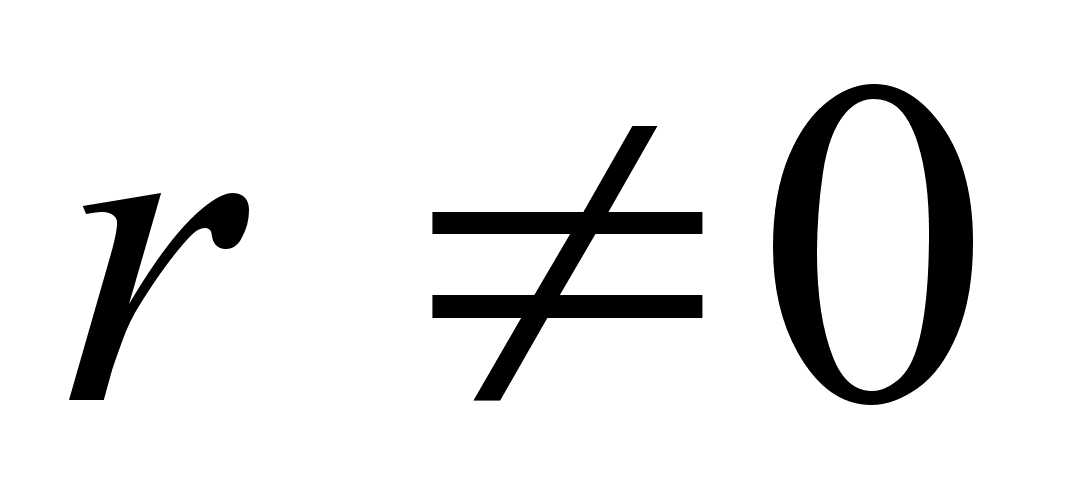 ,
то заменим
пару чисел
,
то заменим
пару чисел
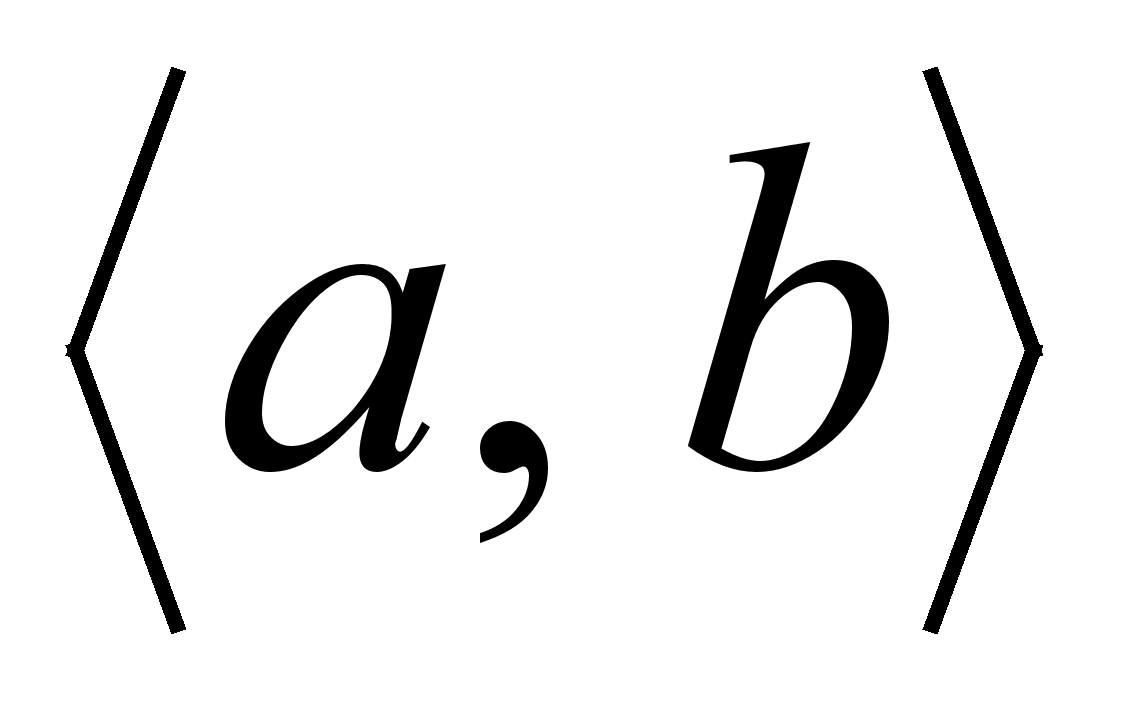 парой
парой
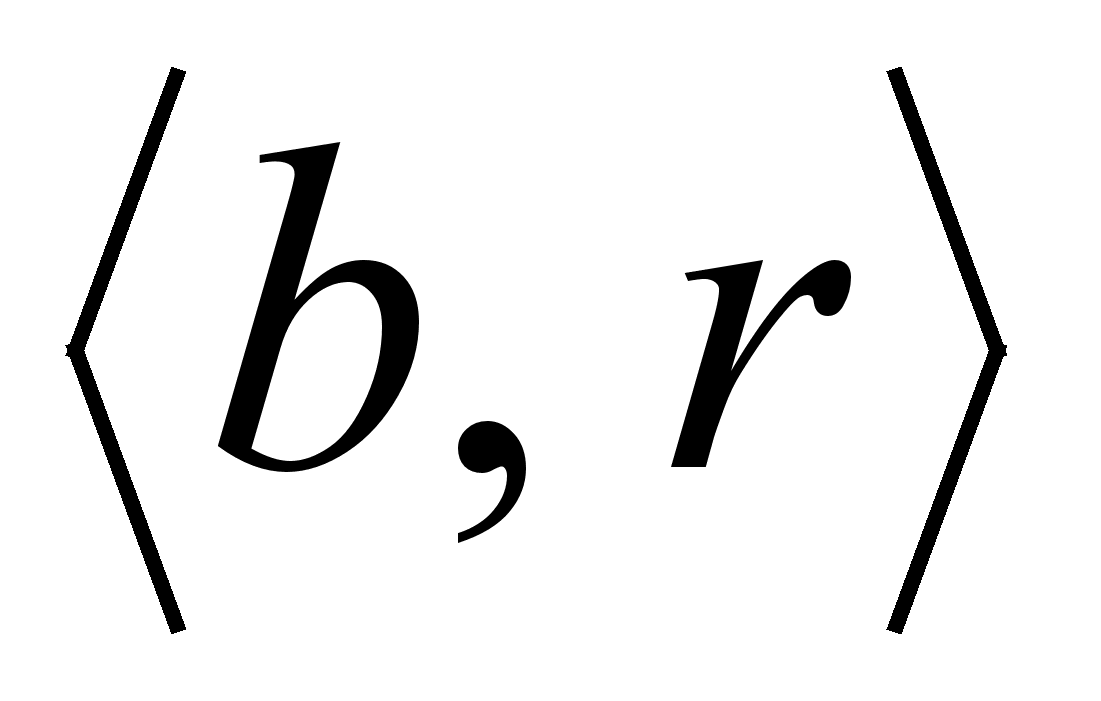 и перейдем
к
и перейдем
к
шагу 1.
Теорема
1. При вычислении
наибольшего
общего делителя
![]() с помощью алгоритма
Евклида будет
выполнено не
более
с помощью алгоритма
Евклида будет
выполнено не
более
![]() операций деления
с остатком, где
операций деления
с остатком, где
![]() есть количество
цифр в десятичной
записи меньшего
из чисел
есть количество
цифр в десятичной
записи меньшего
из чисел
![]() и
и
![]() .
.
Доказательство.
Положим
![]() и определим
и определим
![]() - последовательность
делителей,
появляющихся
в процессе
выполнения
шага 1 алгоритма
Евклида. Тогда
- последовательность
делителей,
появляющихся
в процессе
выполнения
шага 1 алгоритма
Евклида. Тогда
![]() .
.
Пусть также
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
- последовательность
Фибоначчи.
Индукцией по
,
- последовательность
Фибоначчи.
Индукцией по
![]() от
от
![]() до
до
![]() легко доказывается
неравенство
легко доказывается
неравенство
![]() .
А так как
.
А так как
![]() ,
то имеем неравенства
,
то имеем неравенства
![]() и
и
![]() .
.
Немного
подправив
алгоритм Евклида,
можно достаточно
быстро решать
сравнения
![]() при условии,
что
при условии,
что
![]() .
Эта задача
равносильна
поиску целых
решений уравнения
.
Эта задача
равносильна
поиску целых
решений уравнения
![]() .
.
2.2.3.
Алгоритм
решения уравнения
![]()
0) Определим
матрицу
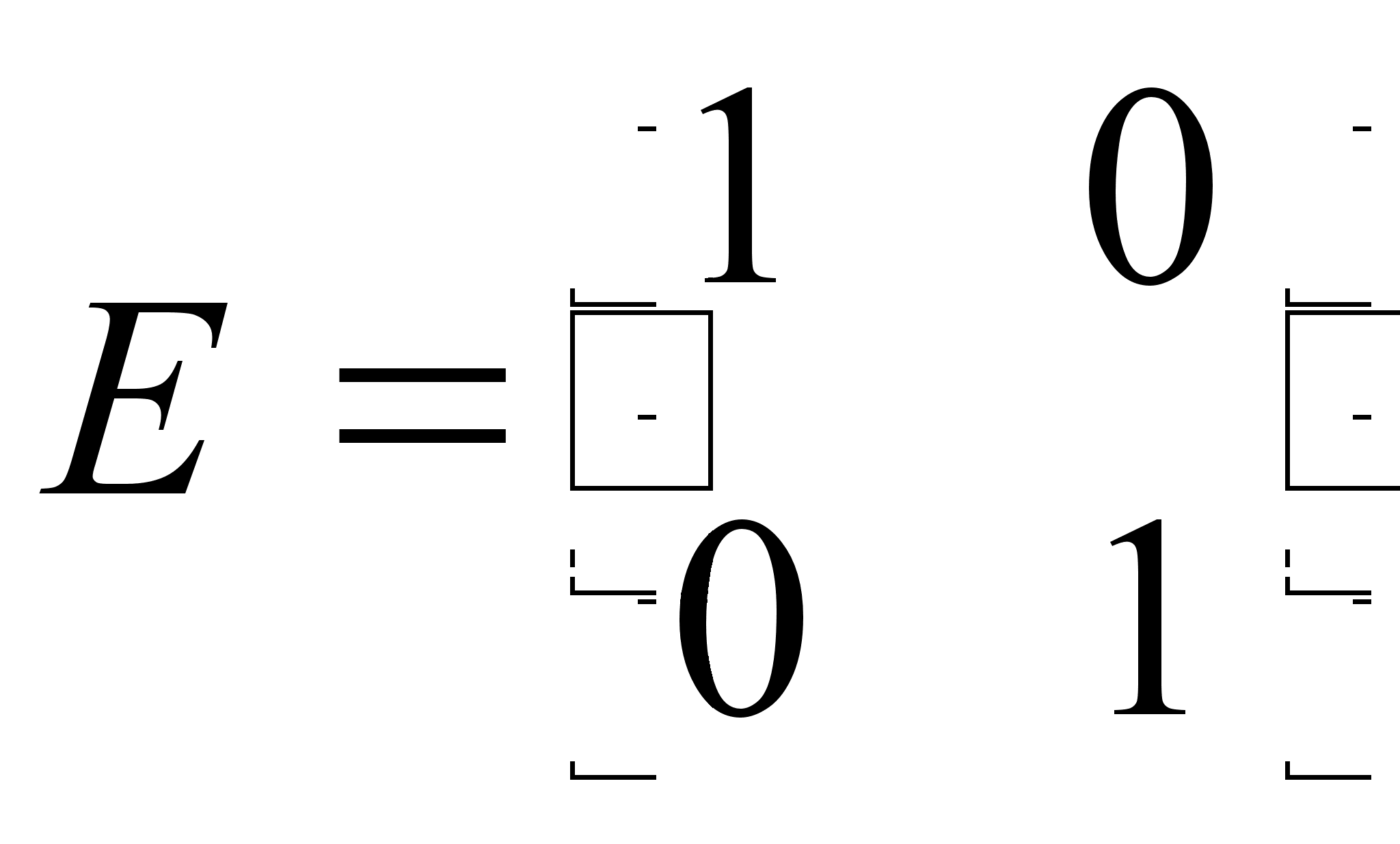 .
.
1) Вычислим
![]() - остаток от
деления числа
- остаток от
деления числа
![]() на
на
![]() ,
,
![]() ,
,
![]() .
.
Если
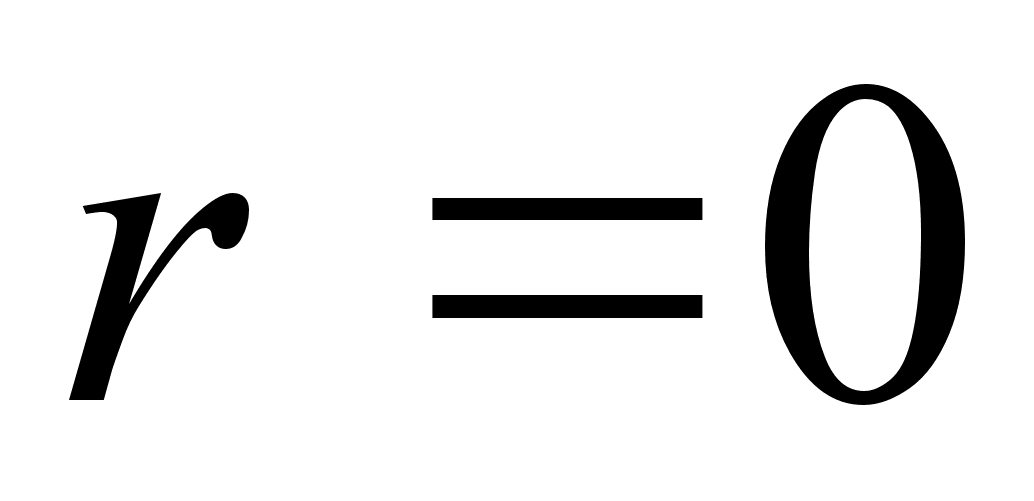 ,
то второй столбец
матрицы
,
то второй столбец
матрицы
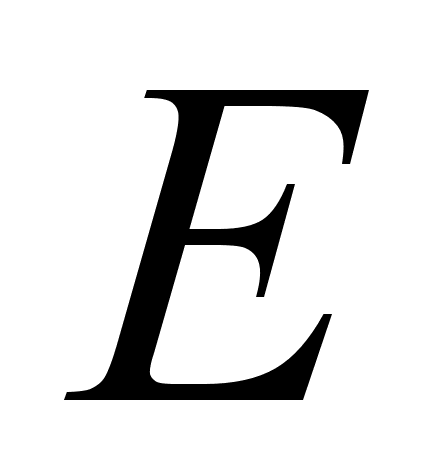 даёт вектор
даёт вектор

решений уравнения.Если
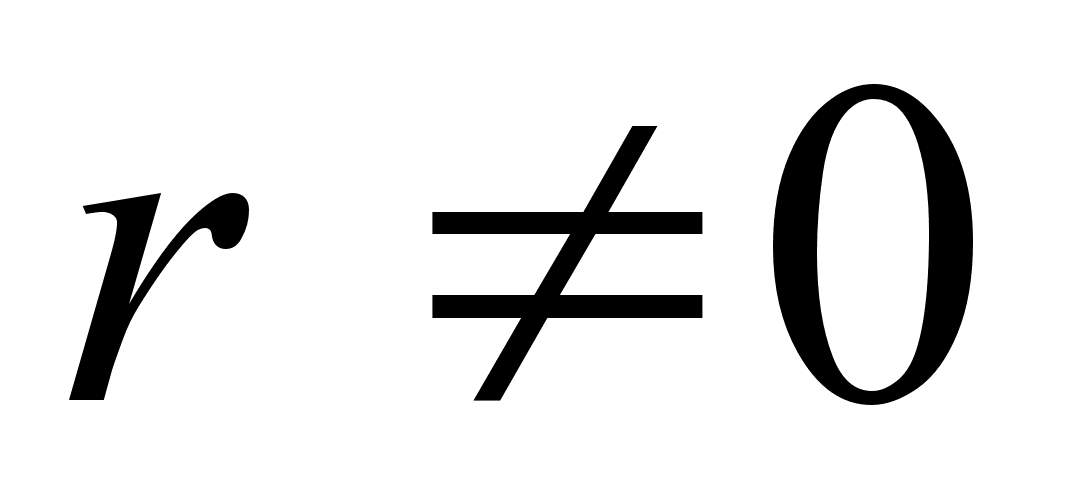 ,
то заменим
матрицу
,
то заменим
матрицу
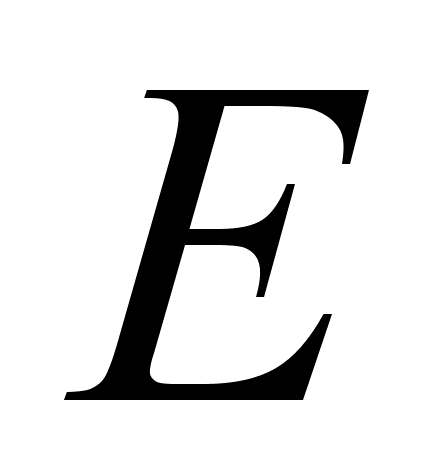 матрицей
матрицей
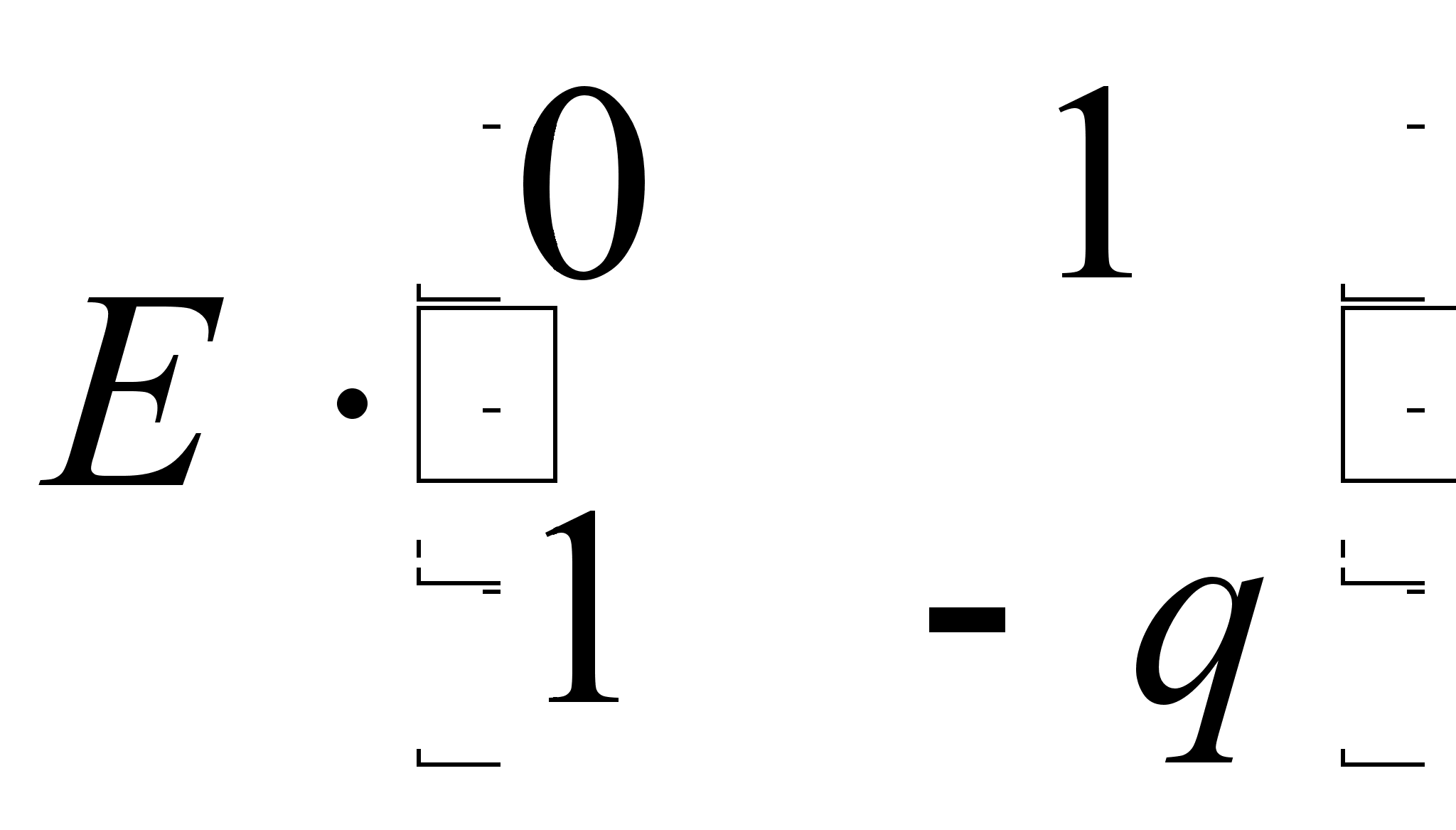 .
.Заменим пару чисел
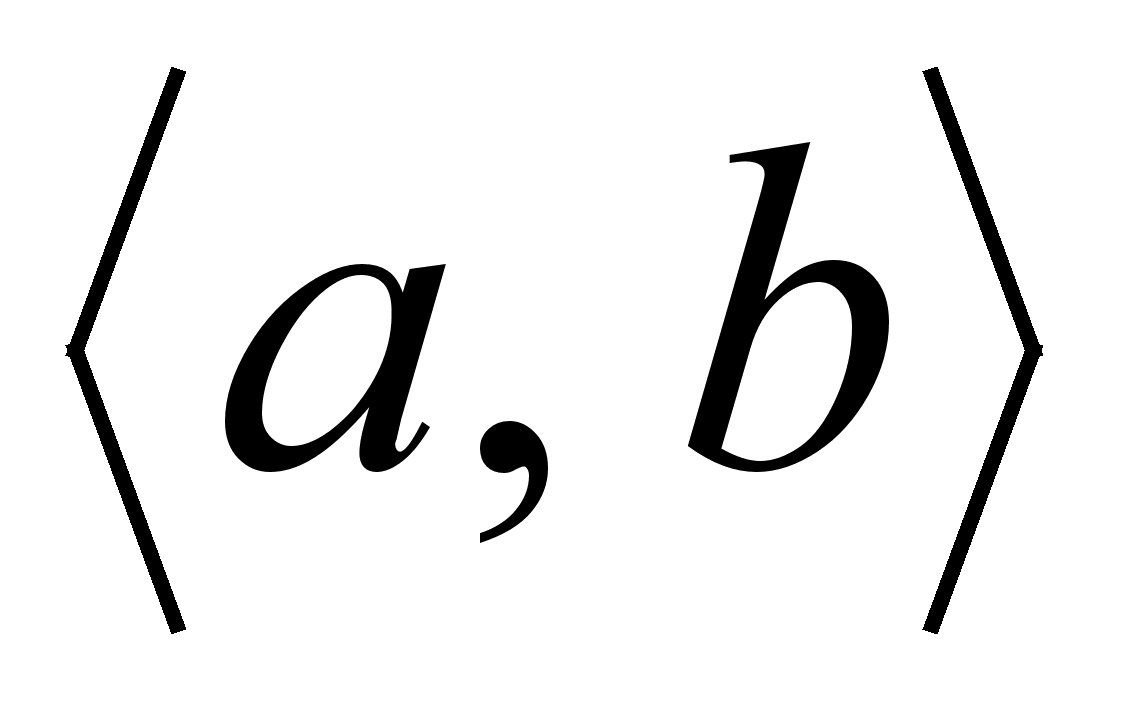 парой
парой
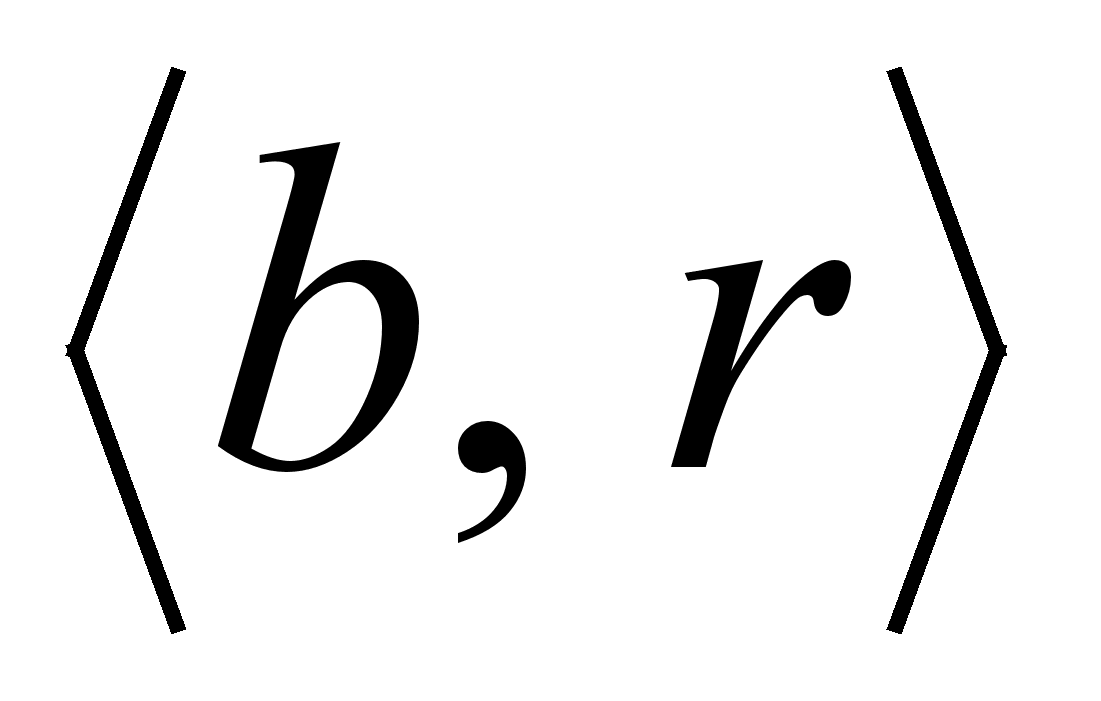 и перейдем к
шагу 1.
и перейдем к
шагу 1.
Если обозначить
через
![]() матрицу
матрицу
![]() ,
возникающую
в процессе
работы алгоритма
перед шагом
2 после
,
возникающую
в процессе
работы алгоритма
перед шагом
2 после
![]() делений с остатком
(шаг 1), то в обозначениях
из доказательства
теоремы 1 в этот
момент выполняется
векторное
равенство
делений с остатком
(шаг 1), то в обозначениях
из доказательства
теоремы 1 в этот
момент выполняется
векторное
равенство
![]() .
Поскольку числа
.
Поскольку числа
![]() и
и
![]() взаимно просты,
имеем
взаимно просты,
имеем
![]() ,
и это доказывает,
что алгоритм
действительно
даёт решение
уравнения
,
и это доказывает,
что алгоритм
действительно
даёт решение
уравнения
![]() .
Буквой
.
Буквой
![]() мы обозначили
количество
делений с остатком,
которое в точности
такое же, как
и в алгоритме
Евклида.
мы обозначили
количество
делений с остатком,
которое в точности
такое же, как
и в алгоритме
Евклида.
Три приведённых
выше алгоритма
относятся к
разряду так
называемых
полиномиальных
алгоритмов.
Это название
носят алгоритмы,
сложность
которых оценивается
сверху степенным
образом в зависимости
от длины записи
входящих чисел.
Если наибольшее
из чисел, подаваемых
на вход алгоритма,
не превосходит
![]() ,
то сложность
алгоритмов
этого типа
оценивается
величиной
,
то сложность
алгоритмов
этого типа
оценивается
величиной
![]() ,
где
,
где
![]() - некоторая
абсолютная
постоянная.
Во всех приведённых
выше примерах
- некоторая
абсолютная
постоянная.
Во всех приведённых
выше примерах
![]() .
.
Полиномиальные алгоритмы в теории чисел - большая редкость. Да и опенки сложности алгоритмов чаше всего опираются на какие-либо не доказанные, но правдоподобные гипотезы, обычно относящиеся к аналитической теории чисел.
Для некоторых задач эффективные алгоритмы вообще не известны. Иногда в таких случаях все же можно предложить последовательность действий, которая, «если повезет», быстро приводит к требуемому результату. Существует класс так называемых вероятностных алгоритмов, которые дают правильный результат, но имеют вероятностную опенку времени работы. Обычно работа этих алгоритмов зависит от одного или нескольких параметров. В худшем случае они работают достаточно долго. Но удачный выбор параметра определяет быстрое завершение работы. Такие алгоритмы, если множество «хороших» значений параметров велико, на практике работают достаточно эффективно, хотя и не имеют хороших опенок сложности.
Мы будем иногда использовать слова детерминированный алгоритм, чтобы отличать алгоритмы в обычном смысле от вероятностных алгоритмов.
Как пример,
рассмотрим
вероятностный
алгоритм, позволяющий
эффективно
находить решения
полиномиальных
сравнений по
простому модулю.
Пусть
![]() — простое число,
которое предполагается
большим, и
— простое число,
которое предполагается
большим, и
![]() - многочлен,
степень которого
предполагается
ограниченной.
Задача состоит
в отыскании
решений сравнения
- многочлен,
степень которого
предполагается
ограниченной.
Задача состоит
в отыскании
решений сравнения
![]() .
(8)
.
(8)
Например,
речь может идти
о решении
квадратичных
сравнений, если
степень многочлена
![]() равна 2. Другими
словами, мы
должны отыскать
в поле
равна 2. Другими
словами, мы
должны отыскать
в поле
![]() все элементы,
удовлетворяющие
уравнению
все элементы,
удовлетворяющие
уравнению
![]() .
.
Согласно
малой теореме
Ферма, все элементы
поля
![]() являются
однократными
корнями многочлена
являются
однократными
корнями многочлена
![]() .
Поэтому, вычислив
наибольший
общий делитель
.
Поэтому, вычислив
наибольший
общий делитель
![]() ,
мы найдем многочлен
,
мы найдем многочлен
![]() ,
множество
корней которого
в поле
,
множество
корней которого
в поле
![]() совпадает с
множеством
корней многочлена
совпадает с
множеством
корней многочлена
![]() ,
причем все эти
корни однократны.
Если окажется,
что многочлен
,
причем все эти
корни однократны.
Если окажется,
что многочлен
![]() имеет нулевую
степень, т. е.
лежит в поле
имеет нулевую
степень, т. е.
лежит в поле
![]() ,
это будет означать,
что сравнение
(8) не имеет решений.
,
это будет означать,
что сравнение
(8) не имеет решений.
Для вычисления
многочлена
![]() удобно сначала
вычислить
многочлен
удобно сначала
вычислить
многочлен
![]() ,
пользуясь
алгоритмом,
подобным описанному
выше алгоритму
возведения
в степень (напомним,
что число
,
пользуясь
алгоритмом,
подобным описанному
выше алгоритму
возведения
в степень (напомним,
что число
![]() предполагается
большим). А затем
с помощью аналога
алгоритма
Евклида вычислить
предполагается
большим). А затем
с помощью аналога
алгоритма
Евклида вычислить
![]() .
Всё это выполняется
за полиномиальное
количество
арифметических
операций.
.
Всё это выполняется
за полиномиальное
количество
арифметических
операций.
Таким
образом, обсуждая
далее задачу
нахождения
решений сравнения
(8), мы можем предполагать,
что в кольце
многочленов
![]() справедливо
равенство
справедливо
равенство
![]()
2.2.4.
Алгоритм нахождения
делителей
многочлена
![]() в кольце
в кольце
![]()
1) Выберем
каким-либо
способом элемент
![]() .
.
Вычислим наибольший общий делитель
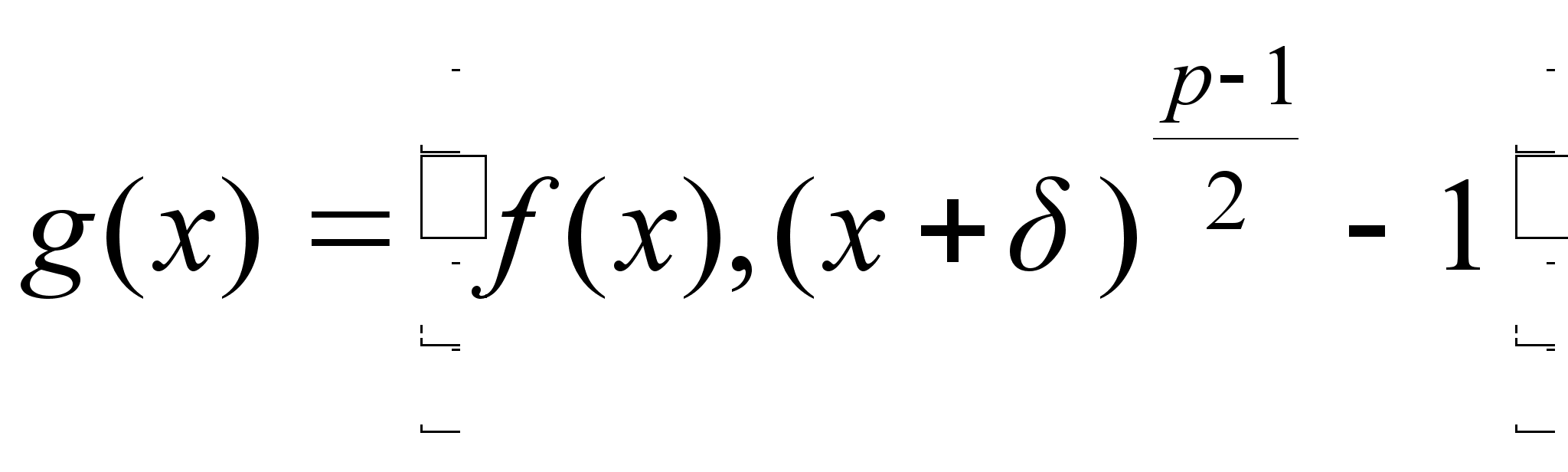 .
.Если многочлен
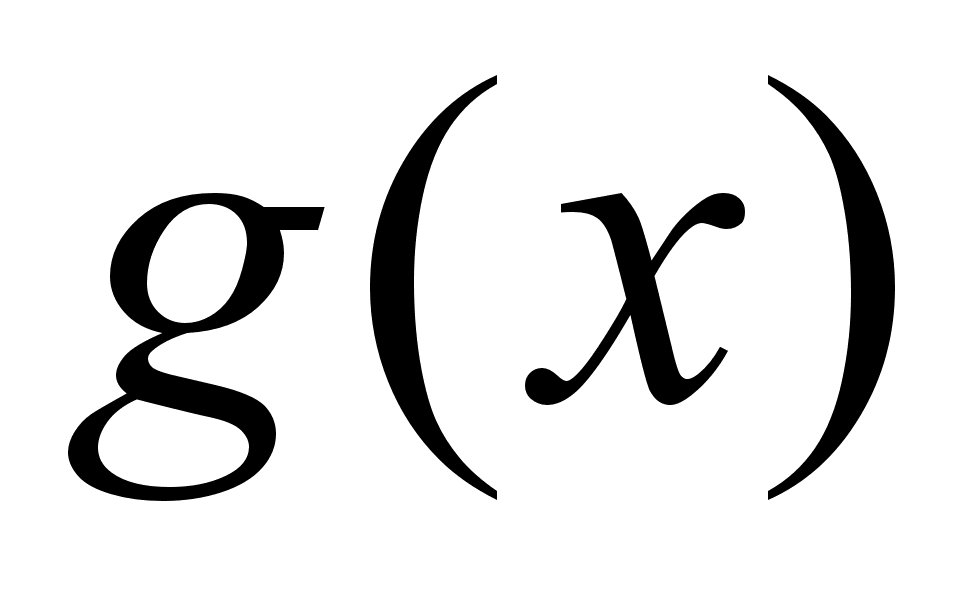 окажется собственным
делителем
окажется собственным
делителем
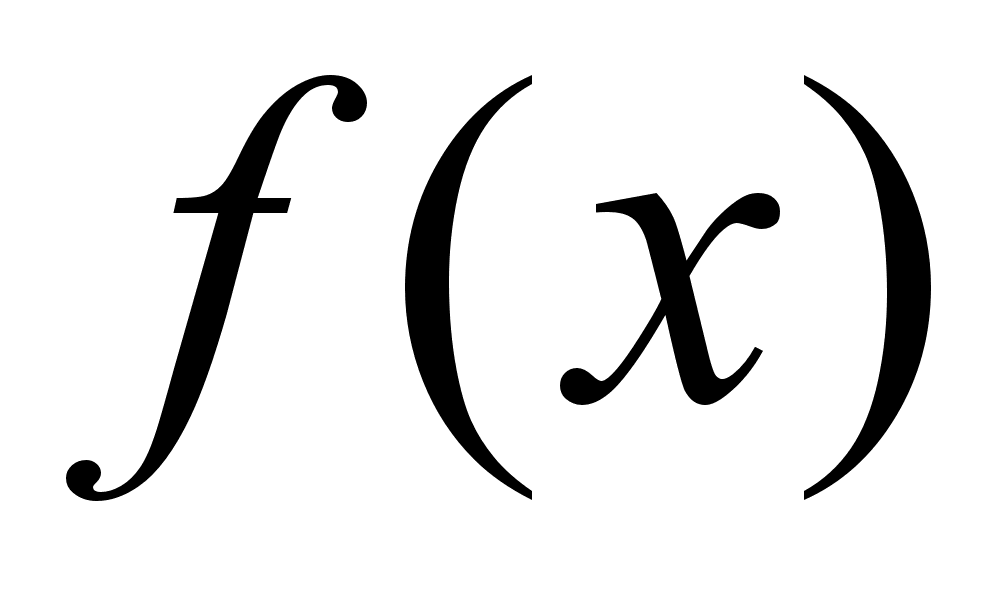 ,
то многочлен
,
то многочлен
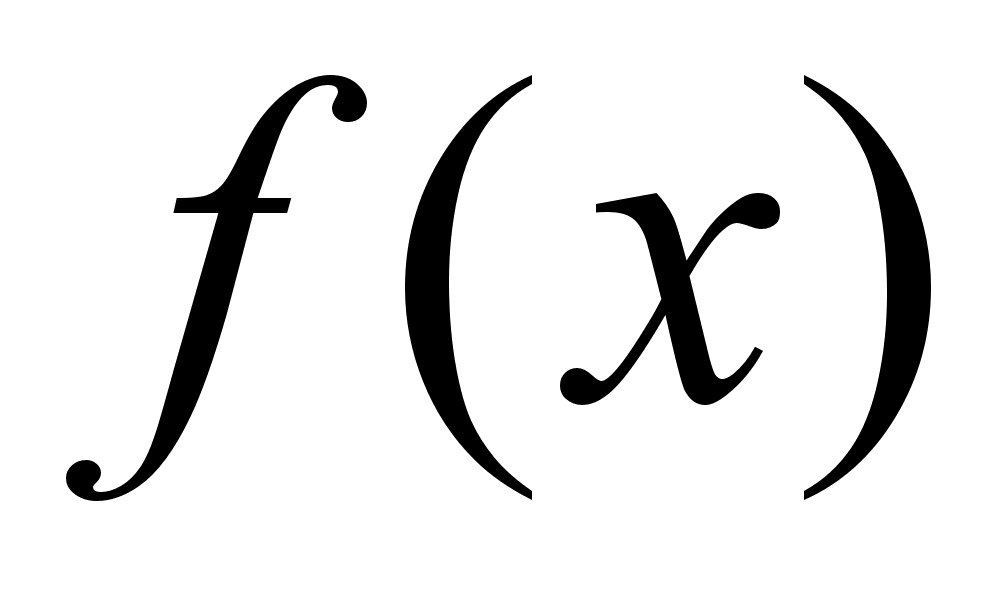 распадётся
на два множителя
и с каждым из
них независимо
нужно будет
проделать все
операции,
предписываемые
настоящим
алгоритмом
для многочлена
распадётся
на два множителя
и с каждым из
них независимо
нужно будет
проделать все
операции,
предписываемые
настоящим
алгоритмом
для многочлена
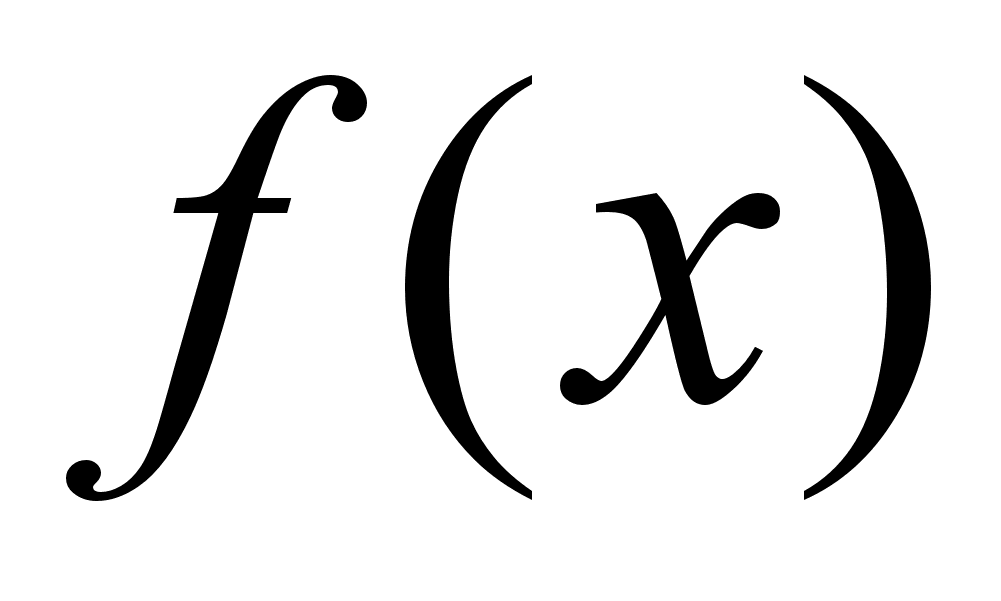 .
.
4) Если окажется,
что
![]() или
или
![]() ,
следует перейти
к шагу 1 и. выбрав
новое значение
,
следует перейти
к шагу 1 и. выбрав
новое значение
![]() ,
продолжить
выполнение
алгоритма.
,
продолжить
выполнение
алгоритма.
Количество
операций на
шаге 2 оценивается
величиной
![]() ,
если вычисления
проводить так,
как это указывалось
выше при нахождении
,
если вычисления
проводить так,
как это указывалось
выше при нахождении
![]() .
Выясним теперь,
сколь долго
придётся выбирать
числа
.
Выясним теперь,
сколь долго
придётся выбирать
числа
![]() ,
пока на шаге
2 не будет найден
собственный
делитель
,
пока на шаге
2 не будет найден
собственный
делитель
![]() .
.
Количество
решений уравнения
![]() в поле
в поле
![]() не превосходит
не превосходит
![]() .
Это означает,
что подмножество
.
Это означает,
что подмножество
![]() элементов
элементов
![]() ,
удовлетворяющих
условиям
,
удовлетворяющих
условиям
![]() ,
,
состоит
не менее, чем
из
![]() элементов.
Учитывая теперь,
что каждый
ненулевой
элемент
элементов.
Учитывая теперь,
что каждый
ненулевой
элемент
![]() удовлетворяет
одному из равенств
удовлетворяет
одному из равенств
![]() ,
либо
,
либо
![]() ,
заключаем, что
для
,
заключаем, что
для
![]() одно из чисел
одно из чисел
![]() будет корнем
многочлена
будет корнем
многочлена
![]() ,
а другое - нет.
Для таких элементов
,
а другое - нет.
Для таких элементов
![]() многочлен
многочлен
![]() ,
определённый
на шаге 2 алгоритма,
будет собственным
делителем
многочлена
,
определённый
на шаге 2 алгоритма,
будет собственным
делителем
многочлена
![]() .
.
Итак, существует
не менее
![]() «удачных»
выборов элемента
«удачных»
выборов элемента
![]() ,
при которых
на шаге 2 алгоритма
многочлен
,
при которых
на шаге 2 алгоритма
многочлен
![]() распадётся
на два собственных
множителя.
Следовательно,
при «случайном»
выборе элемента
распадётся
на два собственных
множителя.
Следовательно,
при «случайном»
выборе элемента
![]() ,
вероятность
того, что многочлен
не разложится
на множители
после
,
вероятность
того, что многочлен
не разложится
на множители
после
![]() повторений
шагов алгоритма
1-4. не превосходит
повторений
шагов алгоритма
1-4. не превосходит
![]() .
Вероятность
с ростом
.
Вероятность
с ростом
![]() убывает очень
быстро. И действительно,
на практике
этот алгоритм
работает достаточно
эффективно.
убывает очень
быстро. И действительно,
на практике
этот алгоритм
работает достаточно
эффективно.
Заметим,
что при опенке
вероятности
мы использовали
только два
корня многочлена
![]() .
При
.
При
![]() эта вероятность,
конечно, еще
меньше. Более
тонкий анализ
с использованием
опенок А. Вейля
для сумм характеров
показывает,
что вероятность
для многочлена
эта вероятность,
конечно, еще
меньше. Более
тонкий анализ
с использованием
опенок А. Вейля
для сумм характеров
показывает,
что вероятность
для многочлена
![]() не распасться
на множители
при однократном
проходе шагов
алгоритма 1-4.
не превосходит
не распасться
на множители
при однократном
проходе шагов
алгоритма 1-4.
не превосходит
![]() .
Здесь постоянная
в
.
Здесь постоянная
в
![]() зависит от
зависит от
![]() .
.
Если в
сравнении (8)
заменить простой
модуль
![]() составным
модулем
составным
модулем
![]() ,
то задача нахождения
решений соответствующего
сравнения
становится
намного более
сложной. Известные
алгоритмы её
решения основаны
на сведении
сравнения к
совокупности
сравнений (8)
по простым
модулям — делителям
,
то задача нахождения
решений соответствующего
сравнения
становится
намного более
сложной. Известные
алгоритмы её
решения основаны
на сведении
сравнения к
совокупности
сравнений (8)
по простым
модулям — делителям
![]() ,
и. следовательно,
они требуют
разложения
числа то на
простые сомножители,
что, как уже
указывалось,
является достаточно
трудоемкой
задачей.
,
и. следовательно,
они требуют
разложения
числа то на
простые сомножители,
что, как уже
указывалось,
является достаточно
трудоемкой
задачей.
3. КАЧЕСТВЕННАЯ ТЕОРИЯ АЛГОРИТМА RSA
Существует
довольно эффективный
способ убедиться,
что заданное
число является
составным, не
разлагая это
число на множители.
Согласно малой
теореме Ферма,
если число
![]() простое, то для
любого целого
простое, то для
любого целого
![]() ,
не делящегося
на
,
не делящегося
на
![]() ,
выполняется
сравнение
,
выполняется
сравнение
![]() .
(9)
.
(9)
Если же
при каком-то
![]() это сравнение
нарушается,
можно утверждать,
что
это сравнение
нарушается,
можно утверждать,
что
![]() - составное.
Проверка (9) не
требует больших
вычислений,
это следует
из алгоритма
1. Вопрос только
в том, как найти
для составного
- составное.
Проверка (9) не
требует больших
вычислений,
это следует
из алгоритма
1. Вопрос только
в том, как найти
для составного
![]() целое число
целое число
![]() ,
не удовлетворяющее
(9). Можно, например,
пытаться найти
необходимое
число
,
не удовлетворяющее
(9). Можно, например,
пытаться найти
необходимое
число
![]() ,
испытывая все
целые числа
подряд, начиная
с 2. Или попробовать
выбирать эти
числа случайным
образом на
отрезке
,
испытывая все
целые числа
подряд, начиная
с 2. Или попробовать
выбирать эти
числа случайным
образом на
отрезке
![]() .
.
К сожалению,
такой подход
не всегда даёт
то, что хотелось
бы. Имеются
составные числа
![]() ,
обладающие
свойством (9)
для любого
целого
,
обладающие
свойством (9)
для любого
целого
![]() с условием
с условием
![]() .
Такие числа
называются
числами Кармайкла.
Рассмотрим,
например, число
.
Такие числа
называются
числами Кармайкла.
Рассмотрим,
например, число
![]() .
Так как 560 делится
на каждое из
чисел 2, 10, 16, то с
помощью малой
теоремы Ферма
легко проверить,
что 561 есть число
Кармайкла.
Можно доказать,
что любое из
чисел Кармайкла
имеет вид
.
Так как 560 делится
на каждое из
чисел 2, 10, 16, то с
помощью малой
теоремы Ферма
легко проверить,
что 561 есть число
Кармайкла.
Можно доказать,
что любое из
чисел Кармайкла
имеет вид
![]() ,
где все простые
,
где все простые
![]() различны, причем
различны, причем
![]() делится на
каждую разность
делится на
каждую разность
![]() .
Лишь недавно,
была решена
проблема о
бесконечности
множества таких
чисел.
.
Лишь недавно,
была решена
проблема о
бесконечности
множества таких
чисел.
В 1976 г. Миллер
предложил
заменить проверку
(9) проверкой
несколько
иного условия.
Если
![]() - простое число,
- простое число,
![]() ,
где
,
где
![]() нечётно, то
согласно малой
теореме Ферма
для каждого
нечётно, то
согласно малой
теореме Ферма
для каждого
![]() с условием
с условием
![]() хотя бы одна
из скобок в
произведении
хотя бы одна
из скобок в
произведении
![]()
делится
на
![]() .
Обращение этого
свойства можно
использовать,
чтобы отличать
составные числа
от простых.
.
Обращение этого
свойства можно
использовать,
чтобы отличать
составные числа
от простых.
Пусть
![]() - нечётное составное
число,
- нечётное составное
число,
![]() ,
где
,
где
![]() нечётно. Назовем
целое число
нечётно. Назовем
целое число
![]() ,
,
![]() ,
«хорошим» для
,
«хорошим» для
![]() ,
если нарушается
одно из двух
условий:
,
если нарушается
одно из двух
условий:
1)
![]() не делится на
не делится на
![]() ;
;
2)
![]() или существует
целое
или существует
целое
![]() ,
,
![]() ,
такое, что
,
такое, что
![]() .
.
Из сказанного
ранее следует,
что для простого
числа
![]() не существует
хороших чисел
не существует
хороших чисел
![]() .
Если же
.
Если же
![]() составное
число, то, как
доказал Рабин,
их существует
не менее
составное
число, то, как
доказал Рабин,
их существует
не менее
![]() .
.
Теперь можно построить вероятностный алгоритм, отличающий составные числа от простых.
3.1. Алгоритм, доказывающий непростоту числа
Выберем случайным образом число
 ,
,
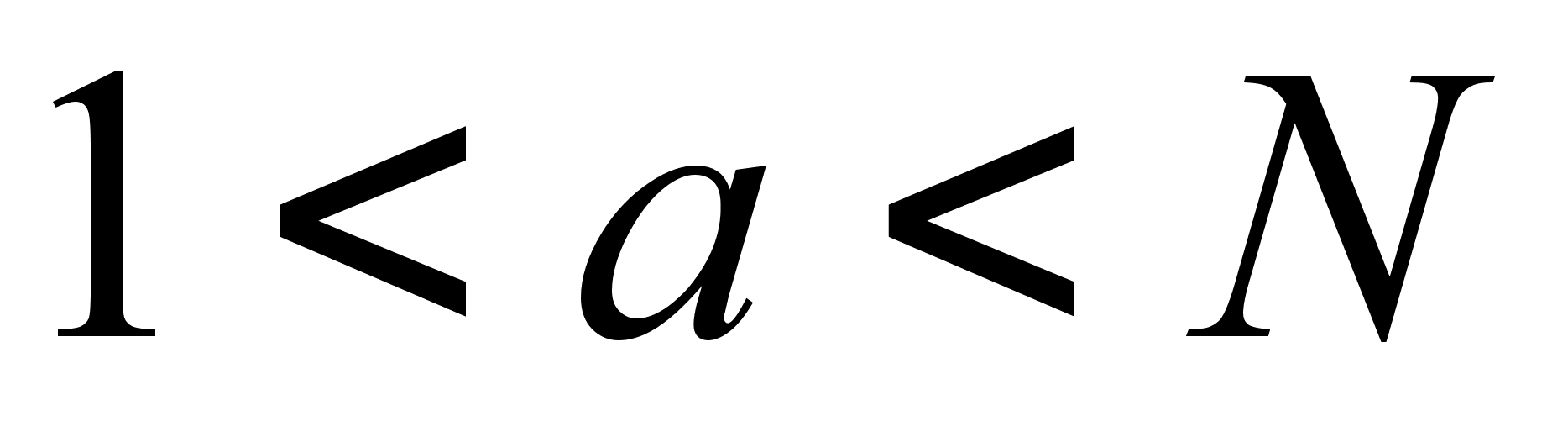 ,
и проверим
для
,
и проверим
для
этого числа указанные выше свойства 1) и 2) п.2.Если хотя бы одно из них нарушается, то число
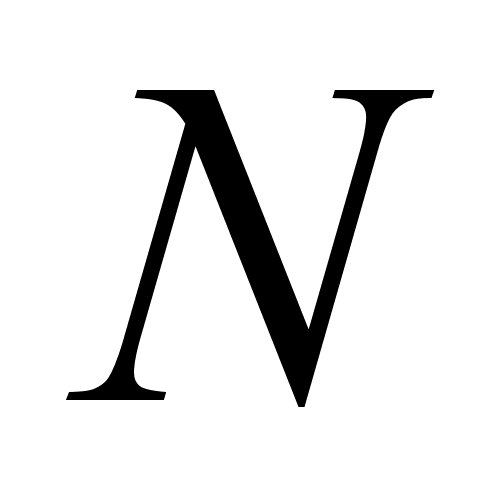 составное.
составное.Если выполнены оба условия 1) и 2) п.2, возвращаемся к шагу 1.
Из сказанного
выше следует,
что составное
число не будет
определено
как составное
после однократного
выполнения
шагов 1-3 с вероятностью
не большей
![]() .
А вероятность
не определить
его после
.
А вероятность
не определить
его после
![]() повторений
не превосходит
повторений
не превосходит
![]() .
т. е. убывает
очень быстро.
.
т. е. убывает
очень быстро.
Миллер
предложил
детерминированный
алгоритм определения
составных
чисел, имеющий
сложность
![]() ,
однако справедливость
его результата
зависит от
недоказанной
в настоящее
время так называемой
расширенной
гипотезы Римана.
Согласно этому
алгоритму
достаточно
проверить
условия 1) и 2) п.2
для всех целых
чисел
,
однако справедливость
его результата
зависит от
недоказанной
в настоящее
время так называемой
расширенной
гипотезы Римана.
Согласно этому
алгоритму
достаточно
проверить
условия 1) и 2) п.2
для всех целых
чисел
![]() ,
,
![]() .
Если при каком-нибудь
.
Если при каком-нибудь
![]() из указанного
промежутка
нарушается
одно из условий
а) или б), число
из указанного
промежутка
нарушается
одно из условий
а) или б), число
![]() составное. В
противном
случае оно
будет простым
или степенью
простого числа.
Последняя
возможность,
конечно, легко
проверяется.
составное. В
противном
случае оно
будет простым
или степенью
простого числа.
Последняя
возможность,
конечно, легко
проверяется.
Напомним
некоторые
понятия, необходимые
для формулировки
расширенной
гипотезы Римана.
Они понадобятся
нам и в дальнейшем.
Пусть
![]() - целое число.
Функция
- целое число.
Функция
![]() называется
характером
Дирихле по
модулю
называется
характером
Дирихле по
модулю
![]() ,
или просто
характером,
если эта функция
периодична
с периодом
,
или просто
характером,
если эта функция
периодична
с периодом
![]() ,
отлична от нуля
только на числах,
взаимно простых
с
,
отлична от нуля
только на числах,
взаимно простых
с
![]() ,
и мультипликативна,
т. е. для любых
целых
,
и мультипликативна,
т. е. для любых
целых
![]() выполняется
равенство
выполняется
равенство
![]() .
Для каждого
.
Для каждого
![]() существует
ровно
существует
ровно
![]() характеров
Дирихле. Они
образуют группу
по умножению.
Единичным
элементом этой
группы является
так называемый
главный характер
характеров
Дирихле. Они
образуют группу
по умножению.
Единичным
элементом этой
группы является
так называемый
главный характер
![]() ,
равный 1 на всех
числах, взаимно
простых с
,
равный 1 на всех
числах, взаимно
простых с
![]() ,
и 0 на остальных
целых числах.
Порядком характера
называется
его порядок
как элемента
мультипликативной
группы характеров.
,
и 0 на остальных
целых числах.
Порядком характера
называется
его порядок
как элемента
мультипликативной
группы характеров.
С каждым
характером
может быть
связана так
называемая
![]() - функция Дирихле
- функция комплексного
переменного
- функция Дирихле
- функция комплексного
переменного
![]() ,
определённая
рядом
,
определённая
рядом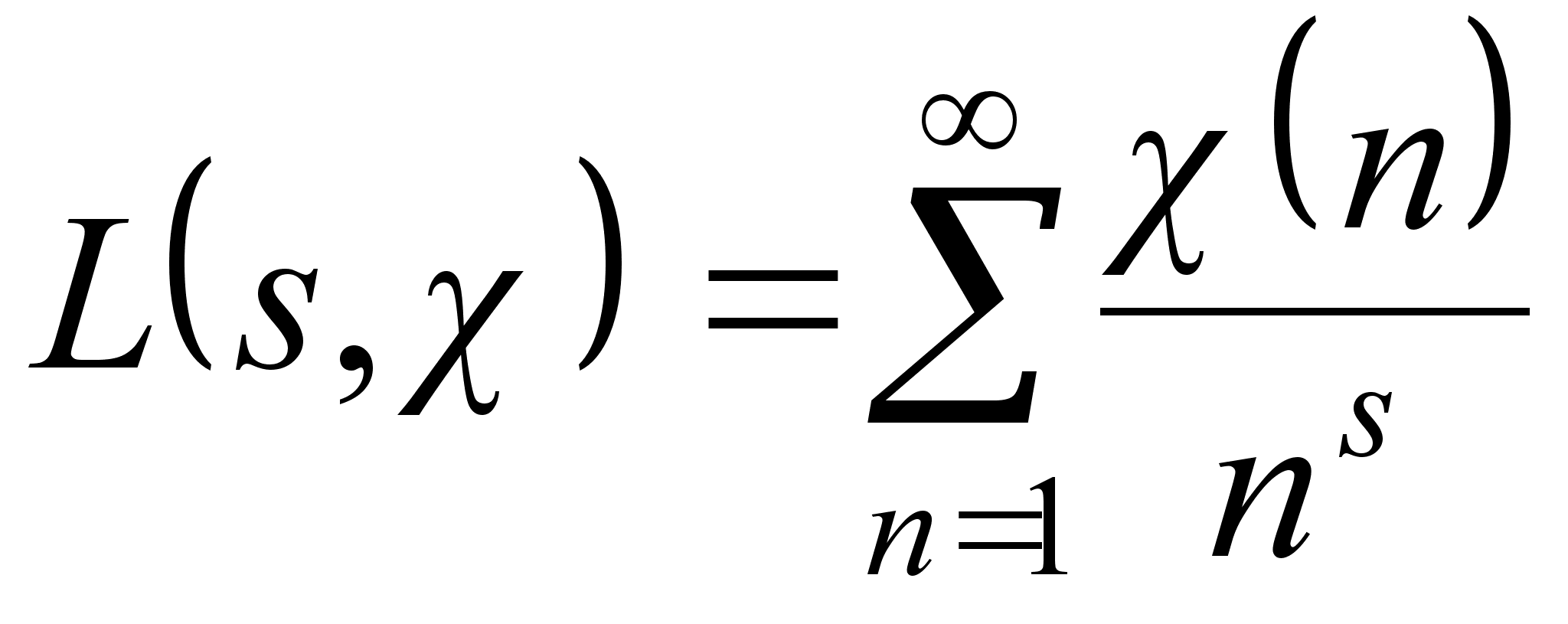 .
Сумма этого
ряда аналитична
в области
.
Сумма этого
ряда аналитична
в области
![]() и может быть
аналитически
продолжена
на всю комплексную
плоскость.
Следующее
соотношение
и может быть
аналитически
продолжена
на всю комплексную
плоскость.
Следующее
соотношение
![]() связывает L
- функцию, отвечающую
главному характеру,
с дзета-функцией
Римана
связывает L
- функцию, отвечающую
главному характеру,
с дзета-функцией
Римана
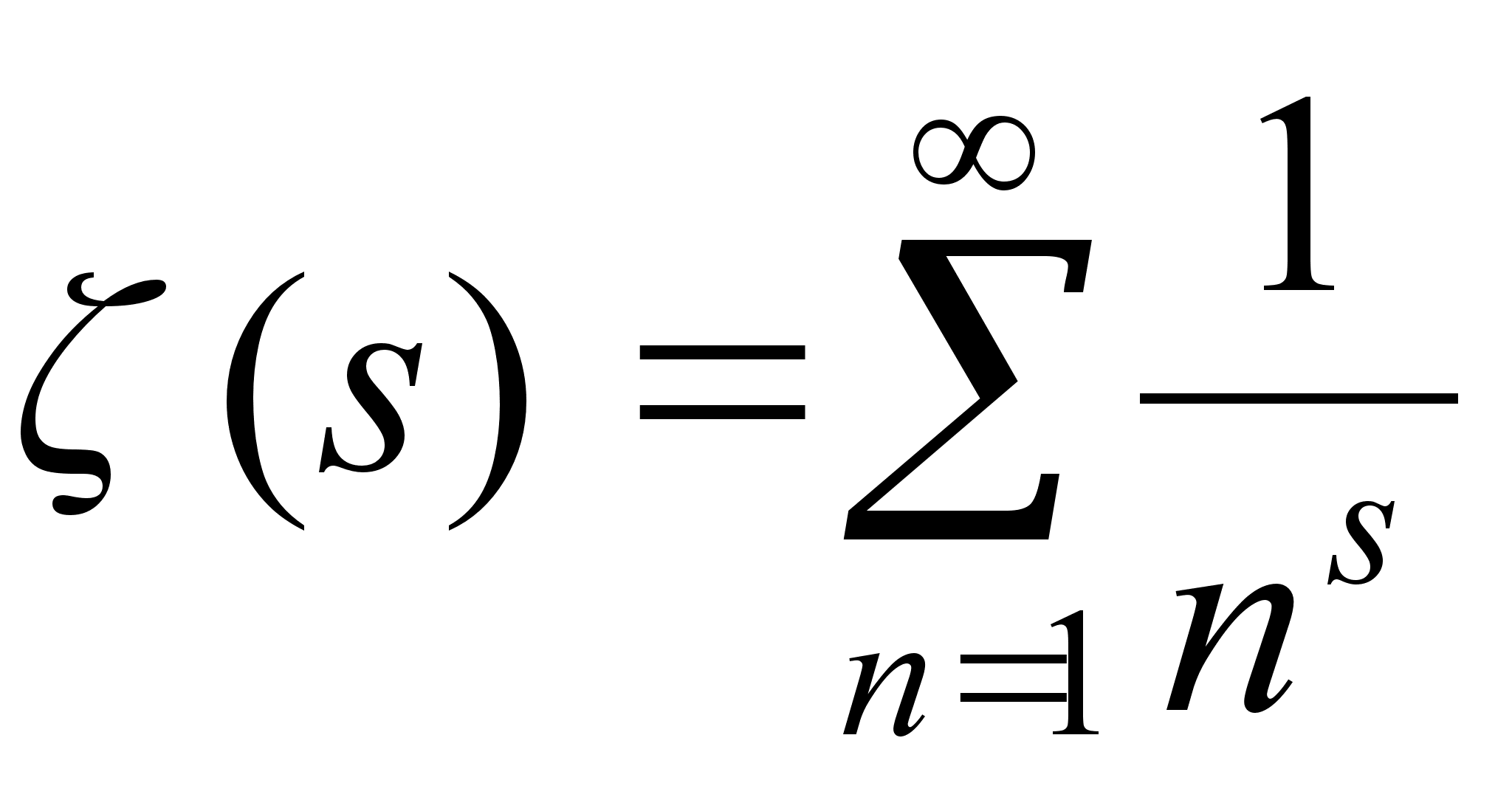 .
Расширенная
гипотеза Римана
утверждает,
что комплексные
нули всех L
-функций Дирихле,
расположенные
в полосе
.
Расширенная
гипотеза Римана
утверждает,
что комплексные
нули всех L
-функций Дирихле,
расположенные
в полосе
![]() ,
лежат на прямой
,
лежат на прямой
![]() .
В настоящее
время не доказана
даже простейшая
форма этой
гипотезы -
классическая
гипотеза Римана,
утверждающая
такой же факт
о нулях дзета-функции.
.
В настоящее
время не доказана
даже простейшая
форма этой
гипотезы -
классическая
гипотеза Римана,
утверждающая
такой же факт
о нулях дзета-функции.
В 1952 г. Анкени
с помощью расширенной
гипотезы Римана
доказал, что
для каждого
простого числа
![]() существует
квадратичный
невычет
существует
квадратичный
невычет
![]() ,
удовлетворяющий
неравенствам
,
удовлетворяющий
неравенствам
![]() .
Константа 70
была сосчитана
позднее. Именно
это утверждение
и лежит в основе
алгоритма
Миллера. В 1957 г.
Берджесс доказал
существование
такого невычета
без использования
расширенной
гипотезы Римана,
но с худшей
оценкой
.
Константа 70
была сосчитана
позднее. Именно
это утверждение
и лежит в основе
алгоритма
Миллера. В 1957 г.
Берджесс доказал
существование
такого невычета
без использования
расширенной
гипотезы Римана,
но с худшей
оценкой
![]() ,
справедливой
при любом
положительном
,
справедливой
при любом
положительном
![]() и
и
![]() ,
большем некоторой
границы, зависящей
от
,
большем некоторой
границы, зависящей
от![]() .
.
Алгоритм
Миллера принципиально
отличается
от алгоритма
2.1., так как полученное
с его помощью
утверждение
о том, что число
![]() - составное,
опирается на
недоказанную
расширенную
гипотезу Римана
и потому может
быть неверным.
В то время как
вероятностный
алгоритм 2.1. даёт
совершенно
правильный
ответ для составных
чисел. Несмотря
на отсутствие
оценок сложности,
на практике
он работает
вполне удовлетворительно.
- составное,
опирается на
недоказанную
расширенную
гипотезу Римана
и потому может
быть неверным.
В то время как
вероятностный
алгоритм 2.1. даёт
совершенно
правильный
ответ для составных
чисел. Несмотря
на отсутствие
оценок сложности,
на практике
он работает
вполне удовлетворительно.
3.2. Нахождение больших простых чисел
Конечно же, большие простые числа можно строить сравнительно быстро. При этом можно обеспечить их случайное распределение в заданном диапазоне величин. В противном случае теряла бы всякий практический смысл система шифрования RSA. Наиболее эффективным средством построения простых чисел является несколько модифицированная малая теорема Ферма.
Теорема
2. Пусть
![]() - нечётные
натуральные
числа,
- нечётные
натуральные
числа,
![]() ,
причем для
каждого простого
делителя
,
причем для
каждого простого
делителя
![]() числа
числа
![]() существует
целое число
существует
целое число
![]() такое, что
такое, что
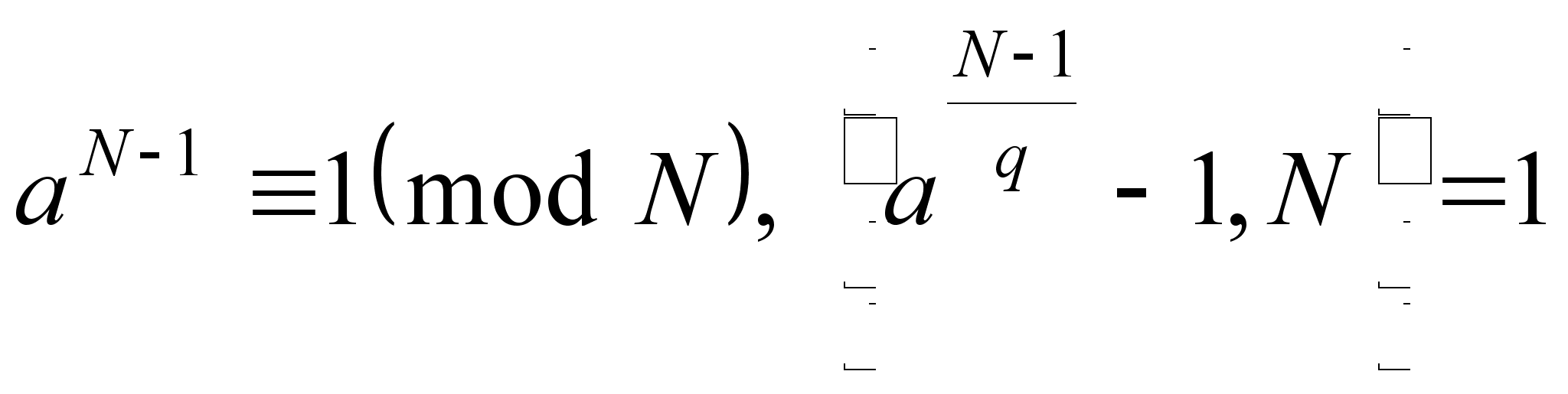 . (10)
. (10)
Тогда каждый
простой делитель
![]() числа
числа
![]() удовлетворяет
сравнению
удовлетворяет
сравнению
![]() .
.
Доказательство.
Пусть
![]() - простой делитель
числа
- простой делитель
числа
![]() ,
a
,
a
![]() - некоторый
делитель
- некоторый
делитель
![]() .
Из условий (10)
следует, что
в поле вычетов
.
Из условий (10)
следует, что
в поле вычетов
![]() справедливы
соотношения
справедливы
соотношения
![]() .
(11)
.
(11)
Обозначим
буквой
![]() порядок элемента
порядок элемента
![]() в мультипликативной
группе поля
в мультипликативной
группе поля
![]() .
Первые два из
соотношений
(11) означают, что
.
Первые два из
соотношений
(11) означают, что
![]() входит в разложение
на простые
множители числа
входит в разложение
на простые
множители числа
![]() в степени такой
же, как и в разложение
в степени такой
же, как и в разложение
![]() ,
а последнее
- что
,
а последнее
- что
![]() делится на
делится на
![]() .
Таким образом,
каждый простой
делитель числа
.
Таким образом,
каждый простой
делитель числа
![]() входит в разложение
входит в разложение
![]() в степени не
меньшей, чем
в
в степени не
меньшей, чем
в
![]() ,
так что
,
так что
![]() делится на
делится на
![]() .
Кроме того,
.
Кроме того,
![]() четно. Теорема
2 доказана.
четно. Теорема
2 доказана.
Следствие.
Если выполнены
условия теоремы
2 и
![]() ,
то
,
то
![]() - простое число.
- простое число.
Действительно,
пусть
![]() равняется
произведению
не менее двух
простых чисел.
Каждое из них,
согласно утверждению
теоремы 2, не
меньше, чем
равняется
произведению
не менее двух
простых чисел.
Каждое из них,
согласно утверждению
теоремы 2, не
меньше, чем
![]() .
Но тогда
.
Но тогда ![]() .
Противоречие
и доказывает
следствие.
.
Противоречие
и доказывает
следствие.
Покажем
теперь, как с
помощью последнего
утверждения,
имея большое
простое число
![]() ,
можно построить
существенно
большее простое
число
,
можно построить
существенно
большее простое
число
![]() .
Выберем для
этого случайным
образом чётное
число
.
Выберем для
этого случайным
образом чётное
число
![]() на промежутке
на промежутке
![]() и положим
и положим
![]() .
Затем проверим
число
.
Затем проверим
число
![]() на отсутствие
малых простых
делителей,
разделив его
на малые простые
числа; испытаем
на отсутствие
малых простых
делителей,
разделив его
на малые простые
числа; испытаем
![]() некоторое
количество
раз с помощью
алгоритма 5.
Если при этом
выяснится, что
некоторое
количество
раз с помощью
алгоритма 5.
Если при этом
выяснится, что
![]() - составное
число, следует
выбрать новое
значение
- составное
число, следует
выбрать новое
значение
![]() и опять повторить
вычисления.
Так следует
делать до тех
пор, пока не
будет найдено
число
и опять повторить
вычисления.
Так следует
делать до тех
пор, пока не
будет найдено
число
![]() ,
выдержавшее
испытания
алгоритмом
5 достаточно
много раз. В
этом случае
появляется
надежда на то,
что
,
выдержавшее
испытания
алгоритмом
5 достаточно
много раз. В
этом случае
появляется
надежда на то,
что
![]() - простое число,
и следует попытаться
доказать простоту
с помощью тестов
теоремы 2.
- простое число,
и следует попытаться
доказать простоту
с помощью тестов
теоремы 2.
Для этого
можно случайным
образом выбирать
число
![]() ,
и проверять
для него выполнимость
соотношений
,
и проверять
для него выполнимость
соотношений
![]() .
(12)
.
(12)
Если при
выбранном
![]() эти соотношения
выполняются,
то, согласно
следствию
из теоремы 2,
можно утверждать,
что число
эти соотношения
выполняются,
то, согласно
следствию
из теоремы 2,
можно утверждать,
что число
![]() простое. Если
же эти условия
нарушаются,
нужно выбрать
другое значение
простое. Если
же эти условия
нарушаются,
нужно выбрать
другое значение
![]() и повторять
эти операции
до тех пор, пока
такое число
не будет обнаружено.
и повторять
эти операции
до тех пор, пока
такое число
не будет обнаружено.
Предположим,
что построенное
число
![]() действительно
является простым.
Зададимся
вопросом, сколь
долго придётся
перебирать
числа
действительно
является простым.
Зададимся
вопросом, сколь
долго придётся
перебирать
числа
![]() ,
пока не будет
найдено такое,
для которого
будут выполнены
условия (12). Заметим,
что для простого
числа
,
пока не будет
найдено такое,
для которого
будут выполнены
условия (12). Заметим,
что для простого
числа
![]() первое условие
(12), согласно малой
теореме Ферма,
будет выполняться
всегда. Те же
числа
первое условие
(12), согласно малой
теореме Ферма,
будет выполняться
всегда. Те же
числа
![]() ,
для которых
нарушается
второе условие
(12), удовлетворяют
сравнению
,
для которых
нарушается
второе условие
(12), удовлетворяют
сравнению
![]() .
Как известно,
уравнение
.
Как известно,
уравнение
![]() в поле вычетов
в поле вычетов
![]() имеет не более
имеет не более
![]() решений. Одно
из них
решений. Одно
из них
![]() .
Поэтому на
промежутке
.
Поэтому на
промежутке
![]() имеется не
более
имеется не
более
![]() чисел, для которых
не выполняются
условия (12). Это
означает, что,
выбирая случайным
образом числа
чисел, для которых
не выполняются
условия (12). Это
означает, что,
выбирая случайным
образом числа
![]() на промежутке
на промежутке
![]() ,
при простом
,
при простом
![]() можно с вероятностью
большей, чем
можно с вероятностью
большей, чем
![]() ,
найти число
,
найти число
![]() ,
для которого
будут выполнены
условия теоремы
2, и тем доказать,
что
,
для которого
будут выполнены
условия теоремы
2, и тем доказать,
что
![]() действительно
является простым
числом.
действительно
является простым
числом.
Заметим,
что построенное
таким способом
простое число
![]() будет удовлетворять
неравенству
будет удовлетворять
неравенству
![]() ,
т. е. будет записываться
вдвое большим
количеством
цифр, чем исходное
простое число
,
т. е. будет записываться
вдвое большим
количеством
цифр, чем исходное
простое число
![]() .
Заменив теперь
число
.
Заменив теперь
число
![]() на найденное
простое число
на найденное
простое число
![]() и повторив с
этим новым
и повторив с
этим новым
![]() все указанные
выше действия,
можно построить
еще большее
простое число.
Начав с какого-нибудь
простого числа,
скажем, записанного
10 десятичными
цифрами (простоту
его можно проверить,
например, делением
на маленькие
табличные
простые числа),
и повторив
указанную
процедуру
достаточное
число раз. можно
построить
простые числа
нужной величины.
все указанные
выше действия,
можно построить
еще большее
простое число.
Начав с какого-нибудь
простого числа,
скажем, записанного
10 десятичными
цифрами (простоту
его можно проверить,
например, делением
на маленькие
табличные
простые числа),
и повторив
указанную
процедуру
достаточное
число раз. можно
построить
простые числа
нужной величины.
Обсудим
теперь некоторые
теоретические
вопросы, возникающие
в связи с нахождением
числа
![]() ,
удовлетворяющего
неравенствам
,
удовлетворяющего
неравенствам
![]() ,
и такого, что
,
и такого, что
![]() - простое число.
Прежде всего,
согласно теореме
Дирихле, доказанной
еще в 1839 г., прогрессия
- простое число.
Прежде всего,
согласно теореме
Дирихле, доказанной
еще в 1839 г., прогрессия
![]() ,
,
![]() содержит бесконечное
количество
простых чисел.
Нас интересуют
простые числа,
лежащие недалеко
от начала прогрессии.
Опенка наименьшего
простого числа
в арифметической
прогрессии
была получена
в 1944 г. Ю. В. Линником.
Соответствующая
теорема утверждает,
что наименьшее
простое число
в арифметической
прогрессии
содержит бесконечное
количество
простых чисел.
Нас интересуют
простые числа,
лежащие недалеко
от начала прогрессии.
Опенка наименьшего
простого числа
в арифметической
прогрессии
была получена
в 1944 г. Ю. В. Линником.
Соответствующая
теорема утверждает,
что наименьшее
простое число
в арифметической
прогрессии
![]() не превосходит
не превосходит
![]() ,
где
,
где
![]() - некоторая
достаточно
большая абсолютная
постоянная.
- некоторая
достаточно
большая абсолютная
постоянная.
Таким
образом, в настоящее
время никаких
теоретических
гарантий для
существования
простого числа
![]() не существует.
Тем не менее
опыт вычислений
на ЭВМ показывает,
что простые
числа в арифметической
прогрессии
встречаются
достаточно
близко к её
началу. Упомянем
в этой связи
гипотезу о
существовании
бесконечного
количества
простых чисел
не существует.
Тем не менее
опыт вычислений
на ЭВМ показывает,
что простые
числа в арифметической
прогрессии
встречаются
достаточно
близко к её
началу. Упомянем
в этой связи
гипотезу о
существовании
бесконечного
количества
простых чисел
![]() с условием, что
число
с условием, что
число
![]() также простое,
т. е. простым
является уже
первый член
прогрессии.
также простое,
т. е. простым
является уже
первый член
прогрессии.
Очень важен
в связи с описываемым
методом построения
простых чисел
также вопрос
о расстоянии
между соседними
простыми числами
в арифметической
прогрессии.
Ведь убедившись,
что при некотором
![]() число
число
![]() составное,
можно следующее
значение
составное,
можно следующее
значение
![]() взять равным
взять равным
![]() и действовать
так далее, пока
не будет найдено
простое число
и действовать
так далее, пока
не будет найдено
простое число
![]() .
И если расстояние
между соседними
простыми числами
в прогрессии
велико, нет
надежды быстро
построить
нужное число
.
И если расстояние
между соседними
простыми числами
в прогрессии
велико, нет
надежды быстро
построить
нужное число
![]() .
Перебор чисел
.
Перебор чисел
![]() до того момента,
как мы наткнемся
на простое
число
до того момента,
как мы наткнемся
на простое
число
![]() окажется слишком
долгим. В более
простом вопросе
о расстоянии
между соседними
простыми числами
окажется слишком
долгим. В более
простом вопросе
о расстоянии
между соседними
простыми числами
![]() и
и
![]() в натуральном
ряде доказано
лишь, что
в натуральном
ряде доказано
лишь, что
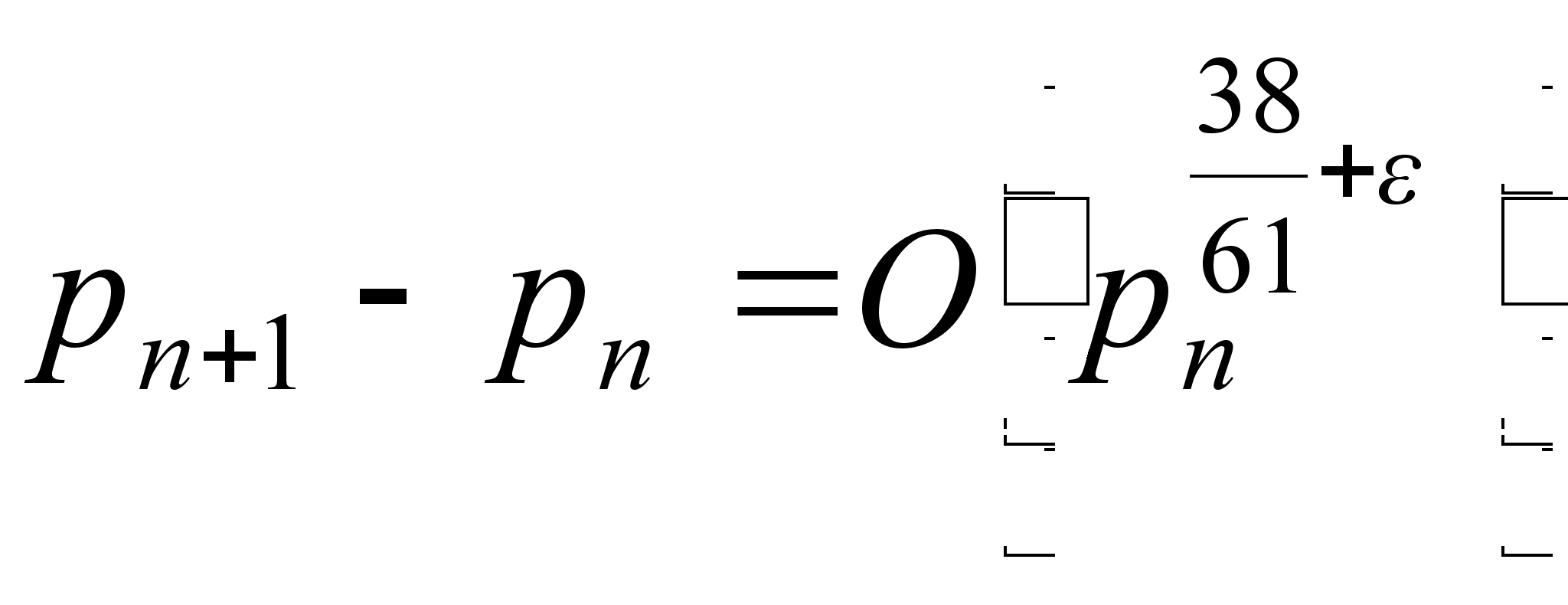 ,
что, конечно,
не очень хорошо
для наших целей.
Вместе с тем
существует
так называемая
гипотеза Крамера
(1936 г.), что
,
что, конечно,
не очень хорошо
для наших целей.
Вместе с тем
существует
так называемая
гипотеза Крамера
(1936 г.), что
![]() ,
дающая вполне
приемлемую
опенку. Примерно
такой же результат
следует и из
расширенной
гипотезы Римана.
Вычисления
на ЭВМ показывают,
что простые
числа в арифметических
прогрессиях
расположены
достаточно
плотно.
,
дающая вполне
приемлемую
опенку. Примерно
такой же результат
следует и из
расширенной
гипотезы Римана.
Вычисления
на ЭВМ показывают,
что простые
числа в арифметических
прогрессиях
расположены
достаточно
плотно.
В качестве
итога обсуждения
в этом пункте
подчеркнём
следующее: если
принять на
веру, что наименьшее
простое число,
а также расстояние
между соседними
простыми числами
в прогрессии
![]() при
при
![]() оцениваются
величиной
оцениваются
величиной
![]() ,
то описанная
схема построения
больших простых
чисел имеет
полиномиальную
опенку сложности.
Кроме того,
несмотря на
отсутствие
теоретических
опенок времени
работы алгоритмов,
отыскивающих
простые числа
в арифметических
прогрессиях
со сравнительно
большой разностью,
на практике
эти алгоритмы
работают вполне
удовлетворительно.
На обычном
персональном
компьютере
без особых
затрат времени
строятся таким
способом простые
числа порядка
,
то описанная
схема построения
больших простых
чисел имеет
полиномиальную
опенку сложности.
Кроме того,
несмотря на
отсутствие
теоретических
опенок времени
работы алгоритмов,
отыскивающих
простые числа
в арифметических
прогрессиях
со сравнительно
большой разностью,
на практике
эти алгоритмы
работают вполне
удовлетворительно.
На обычном
персональном
компьютере
без особых
затрат времени
строятся таким
способом простые
числа порядка
![]() .
.
Конечно, способ конструирования простых чисел для использования в схеме RSA должен быть массовым, а сами простые числа должны быть в каком-то смысле хорошо распределёнными. Это вносит ряд дополнительных осложнений в работу алгоритмов.
Наконец,
отметим, что
существуют
методы построения
больших простых
чисел, использующие
не только простые
делители
![]() ,
но и делители
чисел
,
но и делители
чисел
![]() .
В основе их
лежит использование
последовательностей
целых чисел,
удовлетворяющих
линейным рекуррентным
уравнениям
различных
порядков. Отметим,
что последовательность
.
В основе их
лежит использование
последовательностей
целых чисел,
удовлетворяющих
линейным рекуррентным
уравнениям
различных
порядков. Отметим,
что последовательность
![]() ,
члены которой
присутствуют
в формулировке
малой теоремы
Ферма, составляет
решение рекуррентного
уравнения
первого порядка
,
члены которой
присутствуют
в формулировке
малой теоремы
Ферма, составляет
решение рекуррентного
уравнения
первого порядка
![]() .
.
3.3. Проверка большого числа на простоту
Есть некоторое
отличие в постановках
задач предыдущего
и настоящего
пунктов. Когда
мы строим простое
число
![]() ,
мы обладаем
некоторой
дополнительной
информацией
о нем, возникающей
в процессе
построения.
Например, такой
информацией
является знание
простых делителей
числа
,
мы обладаем
некоторой
дополнительной
информацией
о нем, возникающей
в процессе
построения.
Например, такой
информацией
является знание
простых делителей
числа
![]() .
Эта информация
иногда облегчает
доказательство
простоты
.
Эта информация
иногда облегчает
доказательство
простоты
![]() .
.
В этом пункте
мы предполагаем
лишь, что нам
задано некоторое
число
![]() ,
например, выбранное
случайным
образом на
каком-то промежутке,
и требуется
установить
его простоту,
или доказать,
что оно является
составным. Эту
задачу за
полиномиальное
количество
операций решает
указанный в
п. 3 алгоритм
Миллера. Однако,
справедливость
полученного
с его помощью
утверждения
зависит от
недоказанной
расширенной
гипотезы Римана.
Если число
,
например, выбранное
случайным
образом на
каком-то промежутке,
и требуется
установить
его простоту,
или доказать,
что оно является
составным. Эту
задачу за
полиномиальное
количество
операций решает
указанный в
п. 3 алгоритм
Миллера. Однако,
справедливость
полученного
с его помощью
утверждения
зависит от
недоказанной
расширенной
гипотезы Римана.
Если число
![]() выдержало
испытания
алгоритмом
5 для 100 различных
значений параметра
выдержало
испытания
алгоритмом
5 для 100 различных
значений параметра
![]() ,
то, по-видимому,
можно утверждать,
что оно является
простым с
вероятностью
большей, чем
,
то, по-видимому,
можно утверждать,
что оно является
простым с
вероятностью
большей, чем
![]() .
Эта вероятность
очень близка
к единице, однако
всё же оставляет
некоторую тень
сомнения на
простоте числа
.
Эта вероятность
очень близка
к единице, однако
всё же оставляет
некоторую тень
сомнения на
простоте числа
![]() .
В дальнейшем
в этом пункте
мы будем считать,
что заданное
число
.
В дальнейшем
в этом пункте
мы будем считать,
что заданное
число
![]() является простым,
а нам требуется
лишь доказать
это.
является простым,
а нам требуется
лишь доказать
это.
В настоящее
время известны
детерминированные
алгоритмы
различной
сложности для
доказательства
простоты чисел.
Мы остановимся
подробнее
на одном из
них, предложенном
в 1983 г. в совместной
работе Адлемана.
Померанца и
Рамели. Для
доказательства
простоты или
непростоты
числа
![]() этот алгоритм
требует
этот алгоритм
требует
![]() арифметических
операций. Здесь
арифметических
операций. Здесь
![]() - некоторая
положительная
абсолютная
постоянная.
Функция
- некоторая
положительная
абсолютная
постоянная.
Функция
![]() хоть и медленно,
но всё же возрастает
с ростом
хоть и медленно,
но всё же возрастает
с ростом
![]() ,
поэтому алгоритм
не является
полиномиальным.
Но всё же его
практические
реализации
позволяют
достаточно
быстро тестировать
числа на простоту.
Существенные
усовершенствования
и упрощения
в первоначальный
вариант алгоритма
были внесены
в работах X.
Ленстры и А.
Коена. Мы будем
называть описываемый
ниже алгоритм
алгоритмом
Адлемана - Ленстры.
,
поэтому алгоритм
не является
полиномиальным.
Но всё же его
практические
реализации
позволяют
достаточно
быстро тестировать
числа на простоту.
Существенные
усовершенствования
и упрощения
в первоначальный
вариант алгоритма
были внесены
в работах X.
Ленстры и А.
Коена. Мы будем
называть описываемый
ниже алгоритм
алгоритмом
Адлемана - Ленстры.
В основе
алгоритма лежит
использование
сравнений типа
малой теоремы
Ферма, но в кольцах
целых чисел
круговых полей,
т. е. полей. порождённых
над полем
![]() числами
числами
![]() - корнями из 1.
Пусть
- корнями из 1.
Пусть
![]() - простое нечётное
число и
- простое нечётное
число и
![]() — первообразный
корень по модулю
— первообразный
корень по модулю
![]() ,
т. е. образующий
элемент мультипликативной
группы поля
,
т. е. образующий
элемент мультипликативной
группы поля
![]() ,
которая пиклична.
Для каждого
целого числа
,
которая пиклична.
Для каждого
целого числа
![]() ,
не делящегося
на
,
не делящегося
на
![]() ,
можно определить
его индекс,
,
можно определить
его индекс,
![]() ,
называемый
также дискретным
логарифмом,
с помощью сравнения
,
называемый
также дискретным
логарифмом,
с помощью сравнения
![]() .
Рассмотрим
далее два простых
числа
.
Рассмотрим
далее два простых
числа
![]() ,
,
![]() с условием, что
с условием, что
![]() делится на
делится на
![]() ,
но не делится
на
,
но не делится
на
![]() .
.
Следующая функция, определённая на множестве целых чисел.
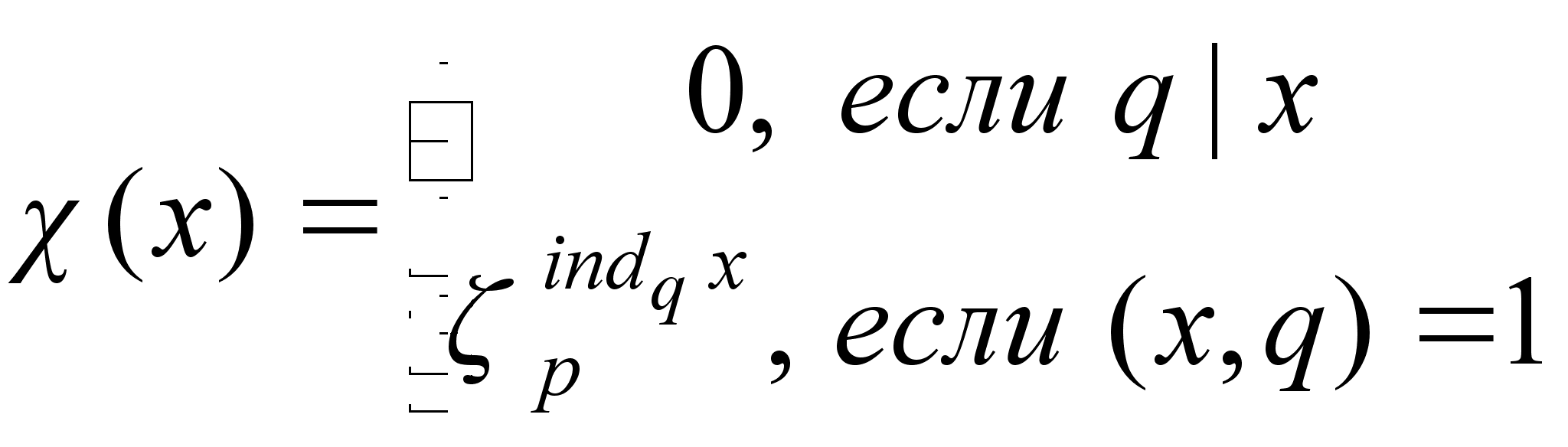
является
характером
по модулю
![]() и порядок этого
характера равен
и порядок этого
характера равен
![]() .
.
Сумма
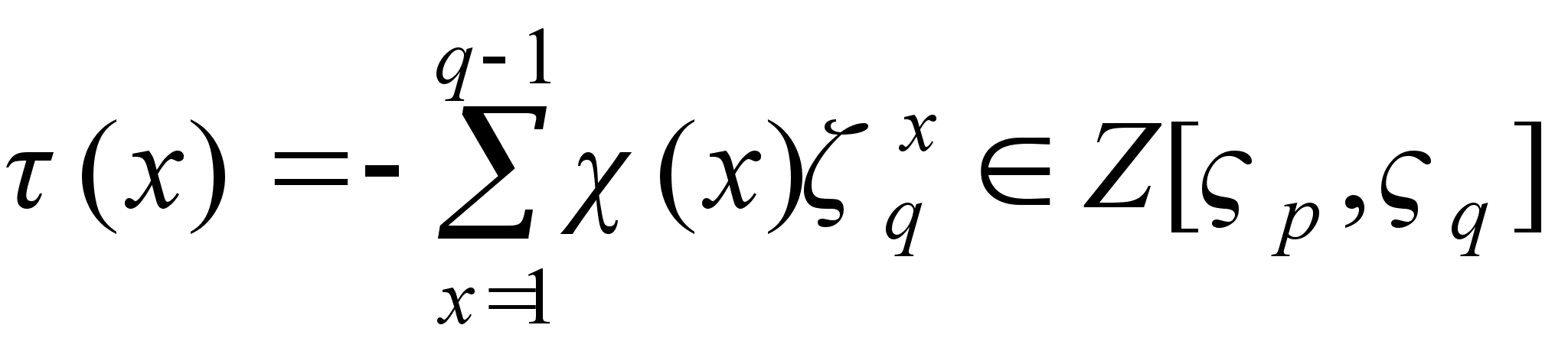
называется суммой Гаусса. Формулируемая ниже теорема 3 представляет собой аналог малой теоремы Ферма, используемый в алгоритме Адлемана - Ленстры.
Теорема
3. Пусть
![]() - нечетное простое
число,
- нечетное простое
число,
![]() .
Тогда в кольце
.
Тогда в кольце
![]() выполняется
сравнение
выполняется
сравнение
![]() .
.
Если при
каких-либо
числах
![]() сравнение из
теоремы 3 нарушается.
можно утверждать,
что
сравнение из
теоремы 3 нарушается.
можно утверждать,
что
![]() составное
число. В противном
случае, если
сравнение
выполняется,
оно даёт некоторую
информацию
о возможных
простых делителях
числа
составное
число. В противном
случае, если
сравнение
выполняется,
оно даёт некоторую
информацию
о возможных
простых делителях
числа
![]() .
Собрав такую
информацию
для различных
.
Собрав такую
информацию
для различных
![]() ,
в конце концов
удаётся установить,
что
,
в конце концов
удаётся установить,
что
![]() имеет лишь один
простой делитель
и является
простым.
имеет лишь один
простой делитель
и является
простым.
В случае
![]() легко проверить,
что сравнение
из теоремы 3
равносильно
хорошо известному
в элементарной
теории чисел
сравнению
легко проверить,
что сравнение
из теоремы 3
равносильно
хорошо известному
в элементарной
теории чисел
сравнению
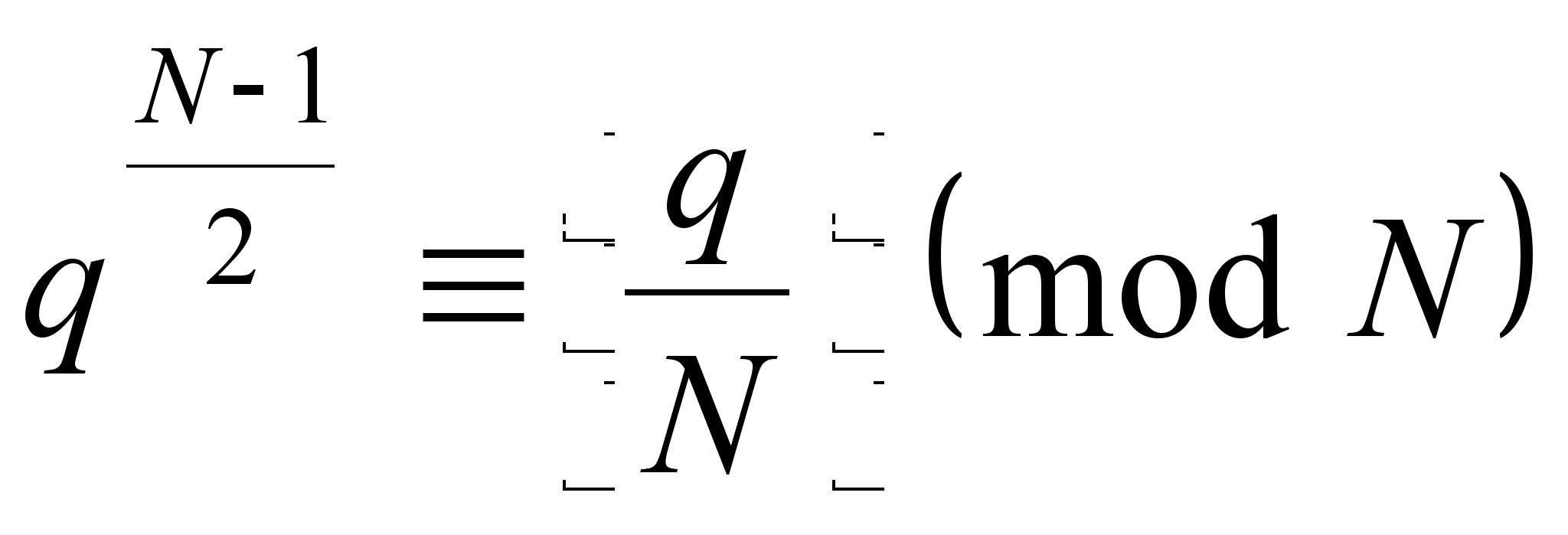 , (13)
, (13)
где
![]() - так называемый
символ Якоби.
Хорошо известно
также, что последнее
сравнение
выполняется
не только для
простых
- так называемый
символ Якоби.
Хорошо известно
также, что последнее
сравнение
выполняется
не только для
простых
![]() ,
но и для любых
целых
,
но и для любых
целых
![]() ,
взаимно простых
с
,
взаимно простых
с
![]() .
Заметим также,
что для вычисления
символа Якоби
существует
быстрый алгоритм,
основанный
на законе взаимности
Гаусса и. в некотором
смысле, подобный
алгоритму
Евклида вычисления
наибольшего
общего делителя.
Следующий
пример показывает.
каким образом
выполнимость
нескольких
сравнений типа
(13) даёт некоторую
информацию
о возможных
простых делителях
числа
.
Заметим также,
что для вычисления
символа Якоби
существует
быстрый алгоритм,
основанный
на законе взаимности
Гаусса и. в некотором
смысле, подобный
алгоритму
Евклида вычисления
наибольшего
общего делителя.
Следующий
пример показывает.
каким образом
выполнимость
нескольких
сравнений типа
(13) даёт некоторую
информацию
о возможных
простых делителях
числа
![]() .
.
Пример
(X.
Ленстра). Пусть
![]() — натуральное
число,
— натуральное
число,
![]() .
для которого
выполнены
сравнения
.
для которого
выполнены
сравнения
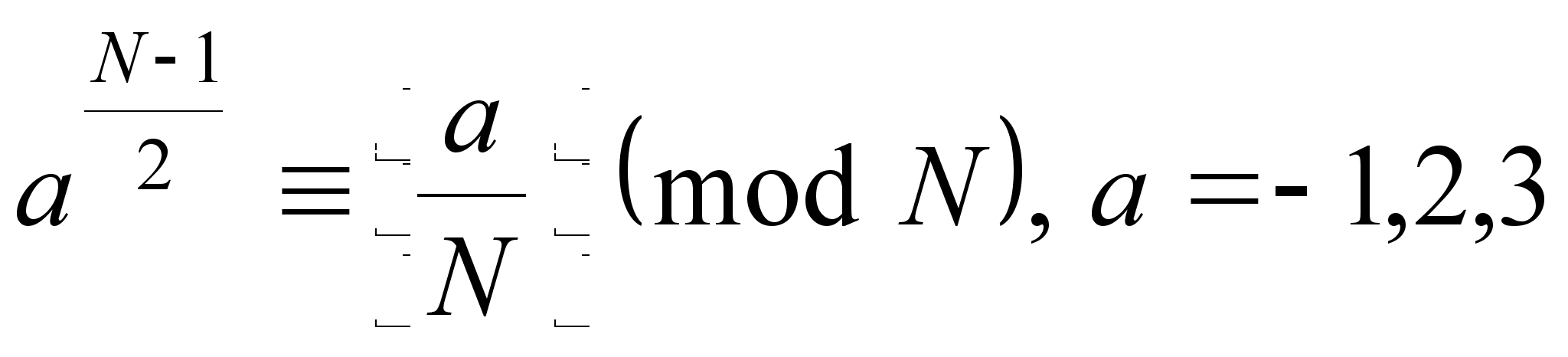 ,
(14)
,
(14)
а кроме
того с некоторым
целым числом
![]() имеем
имеем
![]() .
(15)
.
(15)
Как уже
указывалось,
при простом
![]() сравнения (14)
выполняются
для любого
сравнения (14)
выполняются
для любого
![]() ,
взаимно простого
с
,
взаимно простого
с
![]() ,
а сравнение
(15) означает, что
,
а сравнение
(15) означает, что
![]() есть первообразный
корень по модулю
есть первообразный
корень по модулю
![]() .
Количество
первообразных
корней равно
.
Количество
первообразных
корней равно
![]() ,
т. е. достаточно
велико. Таким
образом, число
,
т. е. достаточно
велико. Таким
образом, число
![]() с условием
(15) при простом
с условием
(15) при простом
![]() может быть
найдено достаточно
быстро с помощью
случайного
выбора и последующей
проверки (15).
может быть
найдено достаточно
быстро с помощью
случайного
выбора и последующей
проверки (15).
Докажем,
что из выполнимости
(14-15) следует, что
каждый делитель
![]() числа
числа
![]() удовлетворяет
одному из сравнений
удовлетворяет
одному из сравнений
![]() или
или
![]() .
(16)
.
(16)
Не уменьшая
общности, можно
считать, что
![]() - простое число.
Введем теперь
обозначения
- простое число.
Введем теперь
обозначения
![]() ,
где
,
где
![]() и
и
![]() - нечётные числа.
Из (15) и сравнения
- нечётные числа.
Из (15) и сравнения
![]() следует, что
следует, что
![]() .
Далее, согласно
(14). выполняются
следующие
сравнения
.
Далее, согласно
(14). выполняются
следующие
сравнения
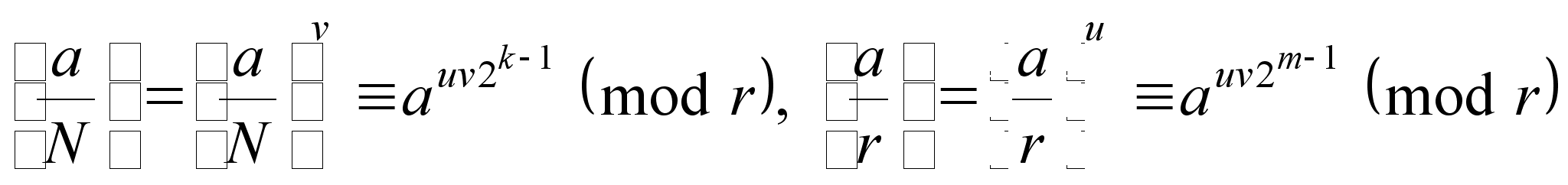 ,
,
означающие (в силу того, что символ Якоби может равняться лишь -1 или +1), что
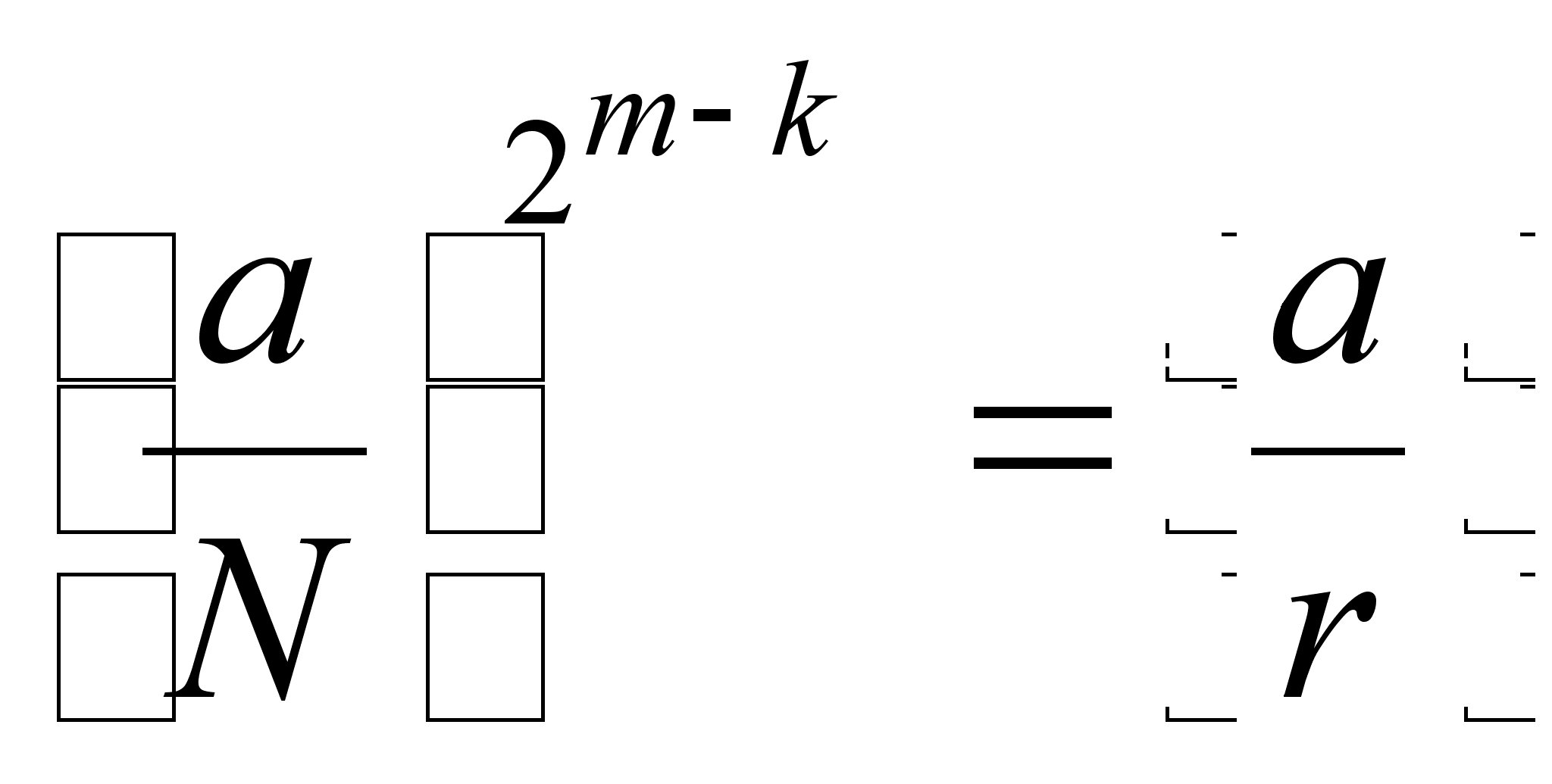 .
.
При
![]() это равенство
означает, что
это равенство
означает, что
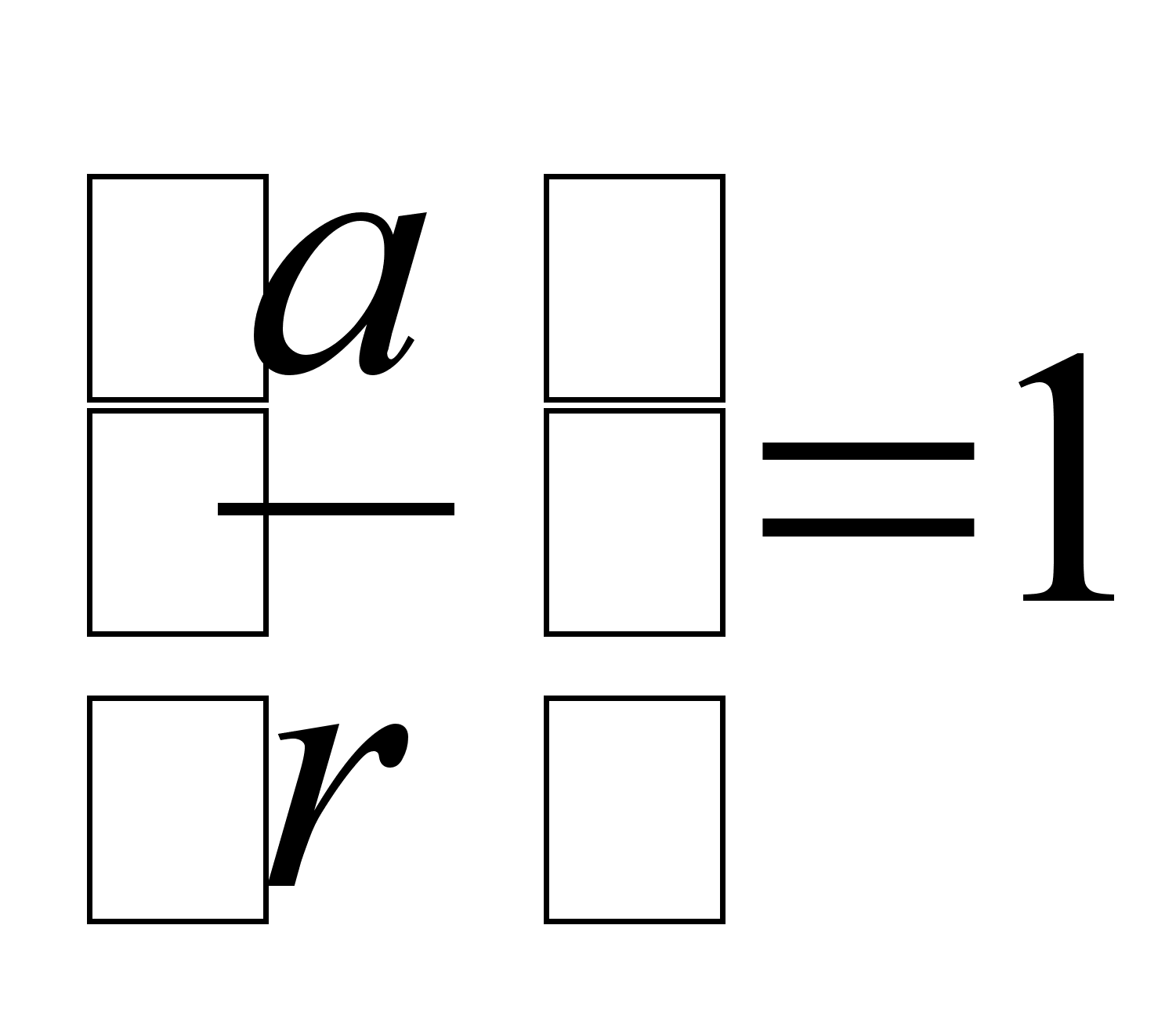 при
при
![]() ,
и, следовательно,
,
и, следовательно,
![]() .
Если же
.
Если же
![]() ,
то имеем
,
то имеем
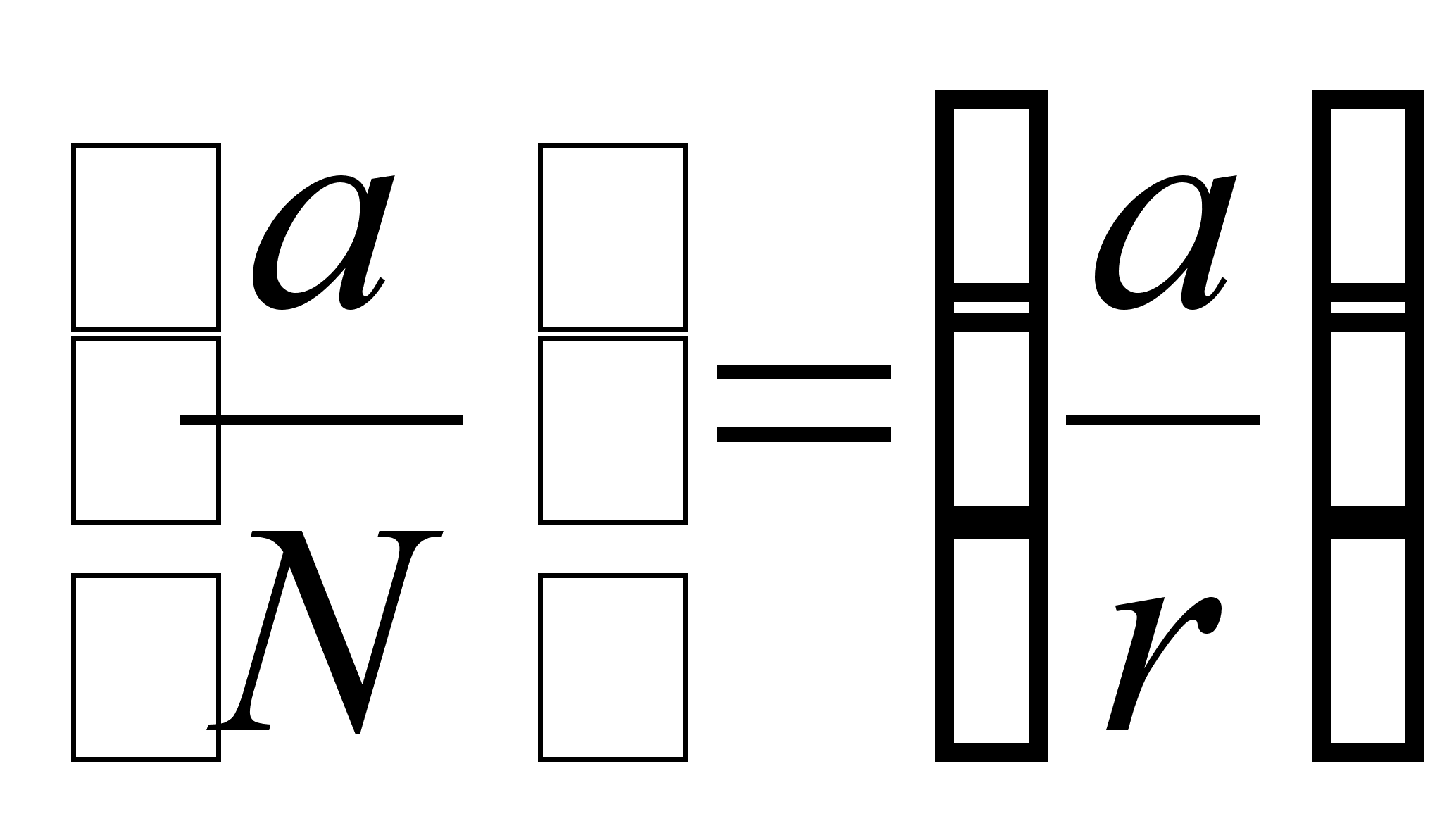 и
и
![]() .
Этим (16) доказано.
.
Этим (16) доказано.
Информация
такого рода
получается
и в случае
произвольных
простых чисел
![]() и
и
![]() с указанными
выше свойствами.
с указанными
выше свойствами.
Опишем
схему алгоритма
Адлемана - Ленстры
для проверки
простоты
![]() :
:
1) выбираются
различные
простые числа
![]() и различные
простые нечётные
и различные
простые нечётные
![]() такие, что
такие, что
1) для каждого
![]() все простые
делители числа
все простые
делители числа
![]() содержатся
содержатся
среди
![]() и
и
![]() не делятся на
квадрат простого
числа;
не делятся на
квадрат простого
числа;
1) ![]() .
.
для каждой пары выбранных чисел
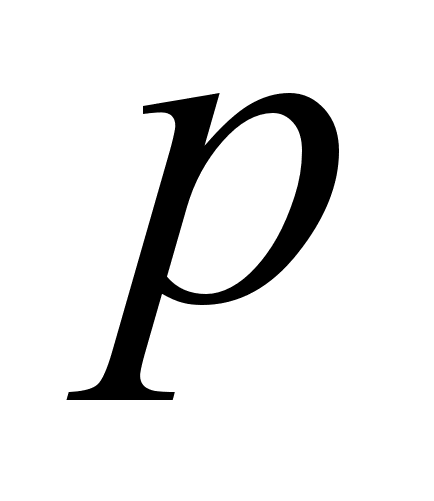 ,
,
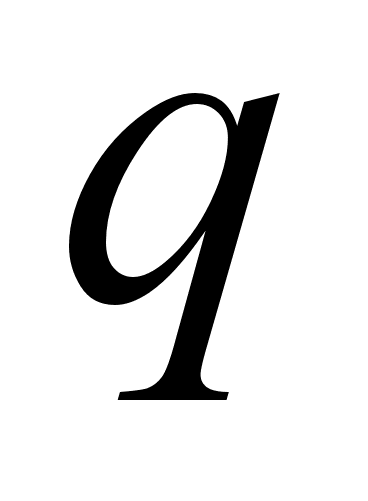 проводятся
тесты, подобные
сравнению из
теоремы 3. Если
проводятся
тесты, подобные
сравнению из
теоремы 3. Если
 не удовлетворяет
какому-либо
из
не удовлетворяет
какому-либо
из
этих тестов - оно составное. В противном случаеопределяется не очень большое множество чисел, с которыми только и могут быть сравнимы простые делители
 .
А именно, каждый
простой делитель
.
А именно, каждый
простой делитель
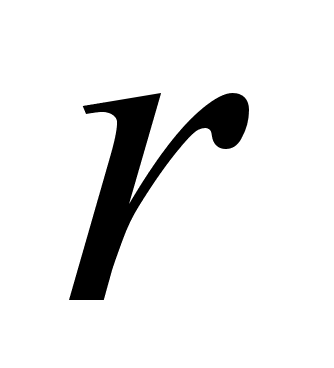 числа
числа
 должен удовлетворять
сравнению вида
должен удовлетворять
сравнению вида
![]() ,
,
![]() .
.
4) проверяется,
содержит ли
найденное
множество
делители
![]() .
Если при этом
делители не
обнаружены,
утверждается,
что
.
Если при этом
делители не
обнаружены,
утверждается,
что
![]() - простое
- простое
число.
Если число
![]() составное, оно
обязательно
имеет простой
делитель
составное, оно
обязательно
имеет простой
делитель
![]() ,
меньший
,
меньший
![]() ,
который сам
содержится
среди возможных
остатков. Именно
на этом свойстве
основано применение
пункта 4) алгоритма.
,
который сам
содержится
среди возможных
остатков. Именно
на этом свойстве
основано применение
пункта 4) алгоритма.
Сумма Якоби
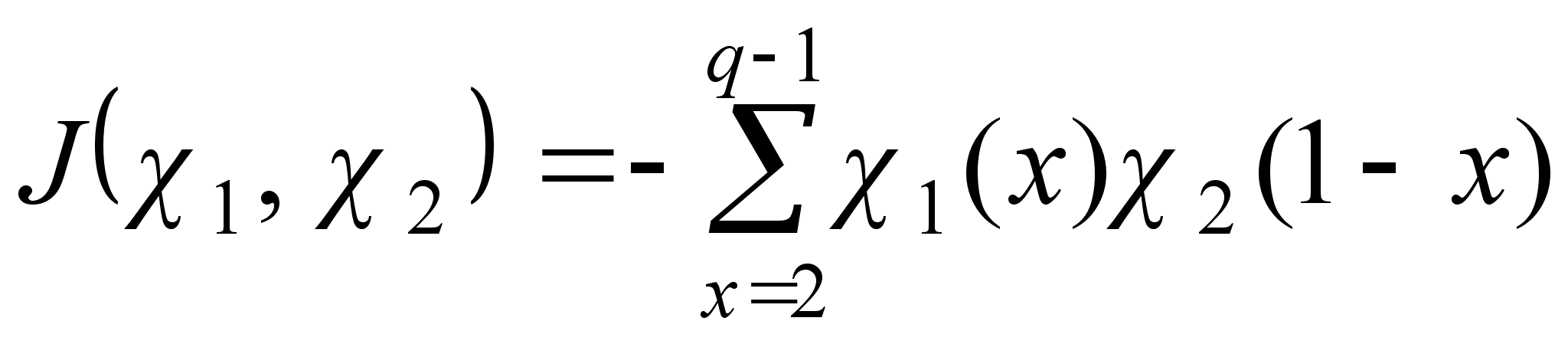
определяется
для двух характеров
![]() модулю
модулю
![]() .
Если характеры
имеют порядок
.
Если характеры
имеют порядок
![]() ,
то соответствующая
сумма Якоби
принадлежит
кольцу
,
то соответствующая
сумма Якоби
принадлежит
кольцу
![]() .
Поскольку числа
.
Поскольку числа
![]() ,
участвующие
в алгоритме,
сравнительно
невелики, то
вычисления
с суммами Якоби
производятся
в полях существенно
меньшей степени,
чем вычисления
с суммами Гаусса.
Это главная
причина, по
которой суммы
Якоби предпочтительнее
для вычислений.
При
,
участвующие
в алгоритме,
сравнительно
невелики, то
вычисления
с суммами Якоби
производятся
в полях существенно
меньшей степени,
чем вычисления
с суммами Гаусса.
Это главная
причина, по
которой суммы
Якоби предпочтительнее
для вычислений.
При
![]() выполняется
классическое
соотношение
выполняется
классическое
соотношение
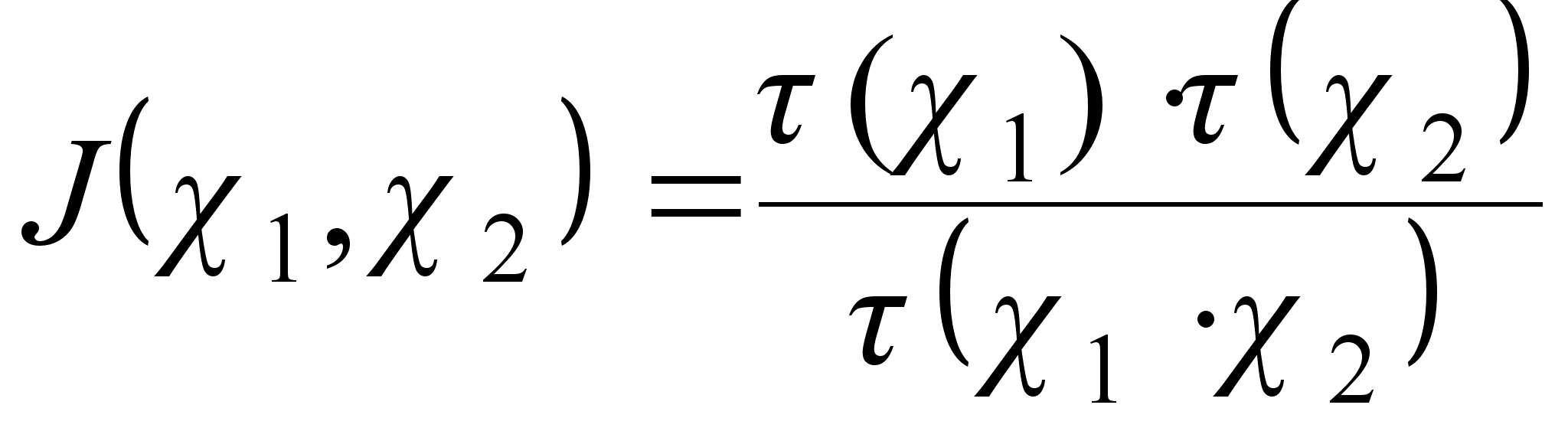
связывающее
суммы Гаусса
с суммами Якоби
и позволяющее
переписать
сравнение
теоремы 3 в терминах
сумм Якоби.
Так. при
![]() и
и
![]() соответствующее
сравнение,
справедливое
для простых
соответствующее
сравнение,
справедливое
для простых
![]() ,
отличных от
2,3,7, принимает
вид
,
отличных от
2,3,7, принимает
вид
![]() ,
,
где
![]() и
и
![]() - некоторый
корень кубический
из 1.
- некоторый
корень кубический
из 1.
В 1984 г. было
внесено существенное
усовершенствование
в алгоритм,
позволившее
освободиться
от требования
неделимости
чисел
![]() на квадраты
простых чисел.
В результате,
например, выбрав
число
на квадраты
простых чисел.
В результате,
например, выбрав
число
![]() и взяв
и взяв
![]() равным произведению
простых чисел
равным произведению
простых чисел
![]() с условием, что
с условием, что
![]() делится на
делится на
![]() ,
получим
,
получим
![]() ,
что позволяет
доказывать
простоту чисел
,
что позволяет
доказывать
простоту чисел
![]() ,
записываемых
сотней десятичных
знаков. При
этом вычисления
будут проводиться
в полях, порождённых
корнями из 1
степеней 16, 9, 5 и
7.
,
записываемых
сотней десятичных
знаков. При
этом вычисления
будут проводиться
в полях, порождённых
корнями из 1
степеней 16, 9, 5 и
7.
Персональный компьютер с процессором Pentium-150. пользуясь реализацией этого алгоритма на языке UBASIC, доказал простоту записываемого 65 десятичными знаками, большего из простых чисел в примере Ривеста, Шамира и Адлемана за 8 секунд. Сравнение этих 8 секунд и 17 лет, потребовавшихся для разложения на множители предложенного в примере числа, конечно, впечатляет.
Отметим,
что опенка
сложности этого
алгоритма
представляет
собой трудную
задачу аналитической
теории чисел.
Как уже указывалось,
количество
операций оценивается
величиной
![]() .
Однако соответствующие
числа
.
Однако соответствующие
числа
![]() и
и
![]() ,
возникающие
в процессе
доказательства,
не могут быть
явно указаны
в зависимости
от
,
возникающие
в процессе
доказательства,
не могут быть
явно указаны
в зависимости
от
![]() .
Доказано лишь
существование
чисел
.
Доказано лишь
существование
чисел
![]() и
и
![]() ,
для которых
достигается
оценка. Впрочем,
есть вероятностный
вариант алгоритма,
доказывающий
простоту простого
числа
,
для которых
достигается
оценка. Впрочем,
есть вероятностный
вариант алгоритма,
доказывающий
простоту простого
числа
![]() с вероятностью
большей
с вероятностью
большей
![]() за
за
![]() арифметических
операций. А в
предположении
расширенной
гипотезы Римана
эта опенка
сложности может
быть получена
при эффективно
указанных
арифметических
операций. А в
предположении
расширенной
гипотезы Римана
эта опенка
сложности может
быть получена
при эффективно
указанных
![]() и
и![]() .
.
4. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ АЛГОРИТМА
Представленный выше алгоритм шифрования был реализован с помощью интегрированного пакета фирмы Borland Delphi 5.0. Выбор данного языка программирования обоснован тем что, он предоставляет такие возможности, как объектно-ориентированный подход к программированию, основанный на формах, интеграция с программированием для Windows и компонентная технология. Среду визуального программирования Delphi 5 позволяет с помощью компонентного подхода к созданию приложений, быстро и качественно "собрать" интерфейс программы и большую часть времени использовать именно на реализацию составленного алгоритма.
Программа построена по технологии клиент/сервер, т.е. клиент передает по сети данные из стандартного потока ввода (с клавиатуры), предварительно зашифровав, сервер, получая поток данных, автоматически его расшифровывает.
Программный
продукт состоит
из двух приложений.
Первое приложение
представляет
собой программу
генерации
ключей. Она
выводит все
простые числа
заданного
диапазона, из
которых потом
выбираются
числа
![]() и
и
![]() .
Там же находятся
открытый и
закрытый ключи,
которые сохраняются
на диске. Второе
приложение,
основная программа,
производит
соединение
между двумя
компьютерами
и, отправляя
сообщение,
шифрует его.
Это приложение
клиент. Приложение
сервер получает
сообщение и
расшифровывает
его. Так же во
второй программе
содержится
небольшая база
данных абонентов,
хранящая в себе
имена абонентов,
IP
адреса и их
открытые ключи.
.
Там же находятся
открытый и
закрытый ключи,
которые сохраняются
на диске. Второе
приложение,
основная программа,
производит
соединение
между двумя
компьютерами
и, отправляя
сообщение,
шифрует его.
Это приложение
клиент. Приложение
сервер получает
сообщение и
расшифровывает
его. Так же во
второй программе
содержится
небольшая база
данных абонентов,
хранящая в себе
имена абонентов,
IP
адреса и их
открытые ключи.
4.1. Реализованные алгоритмы
В программном
продукте были
реализованы
основные алгоритмы
схемы RSA.
Функция ModDegree
производит
вычисление
![]() .
Функция Prost находит
все простые
числа заданного
диапазона.
Функция Evklid реализует
алгоритм Евклида
и находит закрытый
ключ
.
Функция Prost находит
все простые
числа заданного
диапазона.
Функция Evklid реализует
алгоритм Евклида
и находит закрытый
ключ
![]() .
Функция HOD производит
вычисление
наибольшего
общего делителя
и находит открытый
ключ
.
Функция HOD производит
вычисление
наибольшего
общего делителя
и находит открытый
ключ
![]() .
Вышеперечисленные
функции представлены
в приложении
1.
.
Вышеперечисленные
функции представлены
в приложении
1.
4.2. Анализ результатов
Результатом работы созданной программы являются зашифрованные и расшифрованные сообщения.
Для тестирования
программы
использовался
пример приведенный
в [11]
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Также
.
Также
![]() и
и
![]() .
.
5. ВЫВОДЫ
Перейдем к обсуждению выводов после детального просмотра специфики метода, реализованного программного продукта на основе построенного алгоритма, а также представленного анализа результатов по обработанному материалу.
5.1 Алгоритм
Использованный алгоритм RSA имеет ряд преимуществ:
1) алгоритм RSA является ассиметричным, т.е. он основывается на распространении открытых ключей в сети. Это позволяет нескольким пользователям обмениваться информацией, посылаемой по незащищенным каналам связи;
2) пользователь
сам может менять
как числа
![]() ,
,
![]() ,
так и открытый
и закрытый ключ
по своему усмотрению,
только потом
он должен
распространить
открытый ключ
в сети. Это позволяет
добиваться
пользователю
нужной ему
криптостойкости.
,
так и открытый
и закрытый ключ
по своему усмотрению,
только потом
он должен
распространить
открытый ключ
в сети. Это позволяет
добиваться
пользователю
нужной ему
криптостойкости.
При всех этих преимуществах данный алгоритм имеет существенный недостаток – невысокая скорость работы. Алгоритм RSA работает более чем в тысячу раз медленнее симметричного алгоритма DES.
Из всего вышесказанного можно заключить, что данный алгоритм шифрования, хотя довольно медленный, но он ассиметричный и позволяет добиваться нужной криптостойкости, что делает его незаменимым при работе в незащищенных каналах связи.
5.2 Алгоритм и программа
Исходя из проработанных данных, по построенному алгоритму и созданному программному продукту сделаны следующие выводы:
1) построенный алгоритм, а соответственно и созданный на его базе программный продукт, полностью реализует базовые механизмы схемы RSA и, таким образом удовлетворяют основным поставленным задачам;
2) данный программный продукт построен по технологии клиент/сервер и предназначен сохранять конфиденциальность передачи информации в сети.
Таким образом, по выводам о построенном алгоритме и созданном программном продукте можно заключить, что он подходит для решения проблем шифрования информации, связанных с передачей данных по сети.
ЗАКЛЮЧЕНИЕ
В рамках данного дипломного проектирования перед студентом Малышевым А.А. была поставлена задача: на основе алгоритма RSA для шифрования блоков данных, построить алгоритм и реализовать программный продукт для шифрования потоков данных.
В результате выполнения дипломного проектирования был составлен принципиальный алгоритм для решения поставленной задачи. Далее он был детализован и реализован на ЭВМ. В конце, был проведён анализ полученных результатов, и сделаны необходимые выводы.
За основу построения алгоритма был принят алгоритм RSA для шифрования блоков данных, изучена соответствующая литература по алгоритму, и был построен алгоритм и реализован программный продукт в среде визуального программирования Delphi 5 под ОС типа Windows для IBM PC-совместимых компьютеров.
Созданный программный продукт позволяет решить поставленную задачу и, дополнительно, содержит в себе небольшую базу данных абонентов. Т.е. в результате выполнения программы исходное сообщение шифруется и передается по сети, где оно расшифровывается. Также можно указать о том, что программа имеет интуитивно понятный интерфейс, что дополнительно помогает пользователю с наибольшей результативностью использовать всю ресурсную базу.
В заключении, после анализа полученных результатов были сделаны выводы, согласно которым алгоритм работает и применим для поставленной задачи.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Ященко В. В. Основные понятия криптографии // Математическое просвещение. Сер. 3. №2. 1998. С. 53-70.
2. Виноградов И. М. Основы теории чисел. М.: Наука. 1972.
3. Карацуба А. А. Основы аналитической теории чисел. М.: Наука. 1983 г.
4. Кнут Д. Искусство программирования на ЭВМ. Т.2: Получисленные алгоритмы. М.: Мир. 1977.
5. Ахо А.. Хопкрофт Дж.. Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: Мир. 1979.
6. Варновский Н. П. Криптография и теория сложности // Математическое просвещение. Сер. 3. №2. 1998. С. 71-86.
7. Василенко О. Н. Современные способы проверки простоты чисел // Кибернетический сборник, вып. 25. 1988. С. 162-188.
8. Прахар К. Распределение простых чисел. М.: Мир. 1967.
9.Боревич З.И. Шафаревич И.Р. Теория чисел. М.: Наука. 1964.
10. Кострикин А.И. Введение в алгебру. М.: Наука. 1977.
11. Брассар Дж. Современная криптология. Мир ПК. №3. 1997.
ПРИЛОЖЕНИЕ 1
Листинг программы
Модуль Key.pas
Function Prost(n:integer):Boolean;
var k:Boolean;
i:integer;
begin
k:=true;
if n<>2 then
for i:=2 to trunc(sqrt(n))+1 do
if (n/i)=trunc(n/i) then
begin
k:=False;
Break;
end;
Prost:=k;
end;
{________________________________________________________}
Function Evklid(Num1,Num2:integer):integer;
var r,q1,p1:array of integer;
i,n,k:integer;
begin
if Num1>=Num2 then
begin
SetLength(r,10);
r[0]:=Num1;
r[1]:=Num2;
end
else
begin
SetLength(r,10);
r[0]:=Num2;
r[1]:=Num1;
end;
i:=1;
while r[i]<>0 do
begin
inc(i);
r[i]:=r[i-2] mod r[i-1];
end;
n:=i-2;
SetLength(q1,n+1);
for i:=0 to n do
q1[i]:=r[i] div r[i+1];
SetLength(p1,n+2);
p1[0]:=1;
p1[1]:=q1[0];
k:=length(q1);
if k>1 then
for i:=2 to k do
p1[i]:=q1[i-1]*p1[i-1]+p1[i-2];
Result:=trunc(power(-1,k-1))*p1[k-1] mod Num2;
end;
{________________________________________________________}
Function HOD(Num1,Num2:integer):integer;
var r:array of integer;
i:integer;
begin
if Num1>=Num2 then
begin
SetLength(r,Num2);
r[0]:=Num1;
r[1]:=Num2;
end
else
begin
SetLength(r,Num1);
r[0]:=Num2;
r[1]:=Num1;
end;
i:=1;
While r[i]<>0 do
begin
inc(i);
r[i]:=r[i-2] mod r[i-1];
end;
Result:=r[i-1];
end;
{________________________________________________________}
Function ModDegree(Num,Degree,n:integer):integer;
var x:array of integer;
i:integer;
begin
SetLength(x,n);
x[1]:=Num mod n;
for i:=2 to Degree do
x[i]:=x[i-1]*Num mod n;
Result:=x[Degree];
end;
ПРИЛОЖЕНИЕ 2
Главная форма программы
ПРИЛОЖЕНИЕ 3
Форма базы данных абонентов
ПРИЛОЖЕНИЕ 4
Форма нахождения простых чисел и генерации ключей
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет математики и информатики
Кафедра математического анализа и моделирования
Специальность 010200 – “прикладная математика”
ДОПУСТИТЬ К ЗАЩИТЕ
Зав. кафедрой ____________________
___________Т.В.Труфанова
«____»_____________2002 г.
ДИПЛОМНАЯ РАБОТА
на тему Применение алгоритма RSA при шифровании потоков данных
Исполнитель
студент группы 752 А. А. Малышев
Руководитель
к.ф.-м.н., доцент А.Н. Семочкин
Нормоконтроль
к.т.н., доцент А.Н. Гетман
Рецензент
к.ф.-м.н., доцент Е.Ф. Алутина
Благовещенск 2002
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет математики и информатики
Кафедра математического анализа и моделирования
Утверждаю:
Зав. кафедрой
_______________________
подпись И.О.Фамилия
«__»_____________ 200_г.
ЗАДАНИЕ
К дипломной работе студента Малышева Андрея Александровича
1. Тема дипломной работы Применение алгоритма RSA при шифровании потоков данных
(утверждено приказом от ____ №___________)
2. Срок сдачи студентом законченной работы ________________________
3. Исходные данные к дипломной работе ___________________________
4. Содержание дипломной работы (перечень подлежащих разработке вопросов)
Исследовать современные методы шифрования и их приложимость к шифрованию потоков данных. Разработать собственную библиотеку алгоритмов шифрования и программный продукт, демонстрирующий работу этих алгоритмов при передаче данных в сети.
5. Дата выдачи задания « » ____________2002 г.
Руководитель дипломной работы Семочкин Александр Николаевич к.ф.-м.н., доцент кафедры МАиА.
Задание принял к исполнению _____________________________________
РЕФЕРАТ
Дипломная работа 48 стр., 11 источников, 4 приложения.
АЛГОРИТМ RSA, ФУНКЦИЯ ЭЙЛЕРА, ВЗАИМНО ПРОСТЫЕ ЧИСЛА
В данном дипломном проекте рассматривается задача анализа алгоритма шифрование в потоках данных RSA. Для этого построен алгоритм и реализован программный продукт. Программный продукт создан в среде визуального программирования Delphi 5.0, отлажен и протестирован. На основании анализа полученных результатов сделаны выводы, указаны замечания и рекомендации исследователю по практическому использованию программы, а также по дальнейшему улучшению алгоритма и программного продукта в целом.
