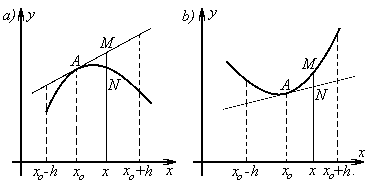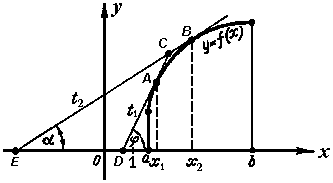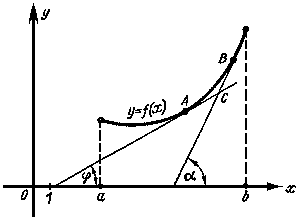Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Приложения производной
Реферат: Приложения производной
Лицей информационных технологий
Реферат
Производная и ее приложения
Выполнил: ученик 11А класса
Новиков А.
Проверила: Шекера Г.В.
г.Хабаровск
2004
Содержание
Введение……………………………………………………………………………………….…3
1. Понятие производной……………………………………………………....………………....4
2. Геометрический смысл производной…………………….………………….......……..4
3. Физический смысл производной……………………………………………………….…….5
4. Правила дифференцирования………………………………………………………….……..6
5. Производные высших порядков……………………………………………………….……..7
6. Изучение функции с помощью производной
6.1.Возрастание и убывание функции. Экстремум функции……………………………..8
6.2.Достаточные условия убывания и возрастания функции.
Достаточные условия экстремума функции………………..…………………...…….11
6.3 .Правило нахождения экстремума………………………………………………….....12
6.4.Точка перегиба графика функции………………………………………………...…...12
6.5.Общая схема исследования функции и построение ее графика……………………..15
6.5. Касательная и нормаль к плоской кривой…………………………..………………..15
7.Экономическое приложение производной.
7.1.Экономическая интерпретация производной………………………………...……….16
7.2. Применение производной в экономической теории...………………………..……..19
7.3. Использование производной для решения задач по экономической теории….…...21
8. Применение производной в физике…………………………………………………….…..23
9. Применение производной в алгебре
9.1. Применение производной к доказательству неравенств…………………………....25
9.2. Применение производной в доказательстве тождеств………………………….…...28
9.3. Применение производной для упрощения алгебраических
и тригонометрических выражений……………………………………………….……29
9.4.Разложение выражения на множители с помощью производной…………………...30
9.5. Применение производной в вопросах существования корней уравнений………....31
Заключение……………………………………………………………………………………...32
Список литературы……………………………………………………………………………..33
Введение
Понятие функции является одним из основных понятии математики. Оно не возникло сразу в таком виде, как мы им пользуемся сейчас, а, как и другие фундаментальные понятия прошло длинный путь диалектического и исторического развития. Идея функциональной зависимости восходит к древнегреческой математике. Например, изменение площади, объема фигуры в зависимости от изменения ее размеров. Однако древними греками идея функциональной зависимости осознавалась интуитивно.
Уже в 16 - 17 в. в, техника, промышленность, мореходство поставили перед математикой задачи, которые нельзя было решить имеющимися методами математики постоянных величин. Нужны были новые математические методы, отличные от методов элементарной математики.
Впервые
термин "функция"
вводит в рассмотрение
знаменитый
немецкий математик
и философ Лейбниц
в
1694 г.
Однако, этот
термин (определения
он не дал вообще)
он употребляет
в узком смысле,
понимая под
функцией изменение
ординаты кривой
в зависимости
от изменения
ее абсциссы.
Таким образом,
понятие функции
носит у него
"геометрический
налет". В современных
терминах это
определение
связано с понятием
множества и
звучит так:
«Функция есть
произвольный
способ отображения
множества А
= {а} во множество
В = {в}, по которому
каждому элементу
а![]() А
поставлен в
соответствие
определенный
элемент в
А
поставлен в
соответствие
определенный
элемент в![]() В.
Уже в этом
определении
не накладывается
никаких ограничений
на закон соответствия
(этот
закон может
быть задан
Формулой, таблицей,
графиком, словесным
описанием).
Главное в этом
определении:
В.
Уже в этом
определении
не накладывается
никаких ограничений
на закон соответствия
(этот
закон может
быть задан
Формулой, таблицей,
графиком, словесным
описанием).
Главное в этом
определении:
![]() а
а![]() А
А![]() !b
!b![]() B.
Под элементами
множеств А и
В понимаются
при этом элементы
произвольной
природы.
B.
Под элементами
множеств А и
В понимаются
при этом элементы
произвольной
природы.
В математике XVII в. самым же большим достижением справедливо считается изобретение дифференциального и интегрального исчисления. Сформировалось оно в ряде сочинений Ньютона и Лейбница и их ближайших учеников. Введение в математику методов анализа бесконечно малых стало началом больших преобразований. Но наряду с интегральными методами складывались и методы дифференциальные. Вырабатывались элементы будущего дифференциального исчисления при решении задач, которые в настоящее время и решаются с помощью дифференцирования. В то время такие задачи были трех видов: определение касательных к кривым, нахождение максимумов и минимумов функций, отыскивание условий существования алгебраических уравнений квадратных корней.
Первый в мире печатный курс дифференциального исчисления опубликовал в 1696 г. Лопиталь. Этот курс состоит из предисловия и 10 глав, в которых излагаются определения постоянных и переменных величин и дифференциала, объясняются употребляющиеся обозначения dx, dy, и др.
Появление анализа бесконечно малых революционизировало всю математику, превратив ее в математику переменных величин.
Исследование поведения различных систем (технические, экономические, экологические и др.) часто приводит к анализу и решению уравнений, включающих как параметры системы, так и скорости их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными.
В своей же работе я хочу подробнее остановится на приложениях производной.
1. Понятие производной
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом
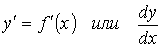
Тот
процесс, с помощью
которого из
данной функции
f(x)
получают новую
функцию f
' (x), называют
дифференцированием
и состоит он
из следующих
трех шагов:
1)
даем аргументу
x
приращение
x
и определяем
соответствующее
приращение
функции y
= f(x+x)
-f(x);
2)
составляем
отношение![]()
3)
считая x
постоянным,
а x
0,
находим![]() ,
который
обозначаем
через f
' (x), как
бы подчеркивая
тем самым, что
полученная
функция зависит
лишь от того
значения x,
при котором
мы переходим
к пределу.
,
который
обозначаем
через f
' (x), как
бы подчеркивая
тем самым, что
полученная
функция зависит
лишь от того
значения x,
при котором
мы переходим
к пределу.
Определение:
Производной
y ' =f ' (x)
данной
функции y=f(x)
при
данном x
называется
предел отношения
приращения
функции к приращению
аргумента при
условии, что
приращение
аргумента
стремится к
нулю, если, конечно,
этот предел
существует,
т.е. конечен.
Таким
образом,
![]() ,
или
,
или
![]()
Заметим,
что если при
некотором
значении x,
например при
x=a,
отношение
![]() при
x0
не стремится
к конечному
пределу, то в
этом случае
говорят, что
функция f(x)
при x=a
(или в точке
x=a)
не имеет производной
или не дифференцируема
в точке x=a.
при
x0
не стремится
к конечному
пределу, то в
этом случае
говорят, что
функция f(x)
при x=a
(или в точке
x=a)
не имеет производной
или не дифференцируема
в точке x=a.
2. Геометрический смысл производной.
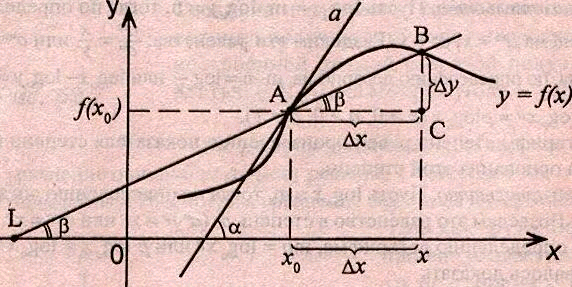
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x0
![]()
f(x)
Рассмотрим произвольную прямую, проходящую через точку графика функции - точку А(x0, f (х0)) и пересекающую график в некоторой точке B(x;f(x)). Такая прямая (АВ) называется секущей. Из ∆АВС: АС = ∆x; ВС =∆у; tgβ=∆y/∆x .
Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO - это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k - угловой коэффициент прямой АВ.
Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.
Если
перейти к пределу
при ∆х → 0 в равенстве
tgβ
=∆y/∆x,
то получим![]() или tg
=f '(x0),
так как
или tg
=f '(x0),
так как
![]() -угол
наклона касательной
к положительному
направлению
оси Ох
-угол
наклона касательной
к положительному
направлению
оси Ох
![]() ,
по определению
производной.
Но tg
= k - угловой коэффициент
касательной,
значит,
k = tg
= f
'(x0).
,
по определению
производной.
Но tg
= k - угловой коэффициент
касательной,
значит,
k = tg
= f
'(x0).
Итак, геометрический смысл производной заключается в следующем:
Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.
3. Физический смысл производной.
Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t0; t0+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.
Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.
lim Vср (t) = (t0) - мгновенная скорость в момент времени t0, ∆t → 0.
а lim = ∆x/∆t = x'(t0) (по определению производной).
Итак, (t) =x'(t).
Физический смысл производной заключается в следующем: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0
Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.
(t) = x'(t) - скорость,
a(f) = '(t) - ускорение, или
a(t) = x"(t).
Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:
φ = φ(t) - изменение угла от времени,
ω = φ'(t) - угловая скорость,
ε = φ'(t) - угловое ускорение, или ε = φ"(t).
Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:
m = m(х) - масса,
x [0; l], l - длина стержня,
р = m'(х) - линейная плотность.
С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука
F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω2 =k/m, получим дифференциальное уравнение пружинного маятника х"(t) + ω2x(t) = 0,
где ω = √k/√m частота колебаний (l/c), k - жесткость пружины (H/m).
Уравнение вида у" + ω2y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция
у = Asin(ωt + φ0) или у = Acos(ωt + φ0), где
А - амплитуда колебаний, ω - циклическая частота,
φ0 - начальная фаза.
4. Правила дифференцирования
| (C)’= 0 С=const |
|
|
|
|
| (cos x)'=-sin x |
|
| (sin x)'=cos x |
|
|
(tg
x)'= |
(ах)'=аx ln a |
|
(ctg
x)'=- |
(ех)'=ex |
|
|
![]()
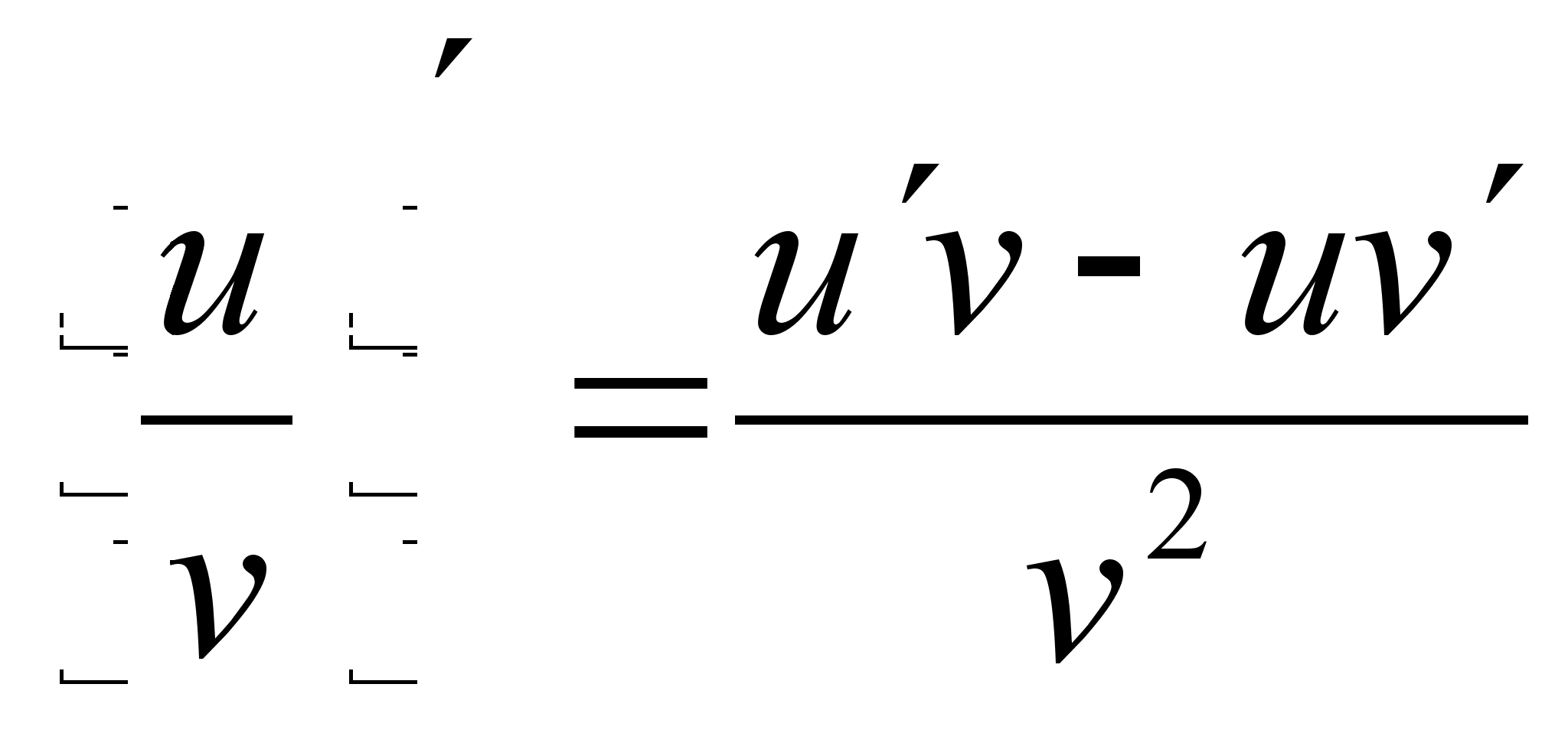
![]()
![]()
Производная степенно-показательной функции
![]() ,
где
,
где
![]() .
.
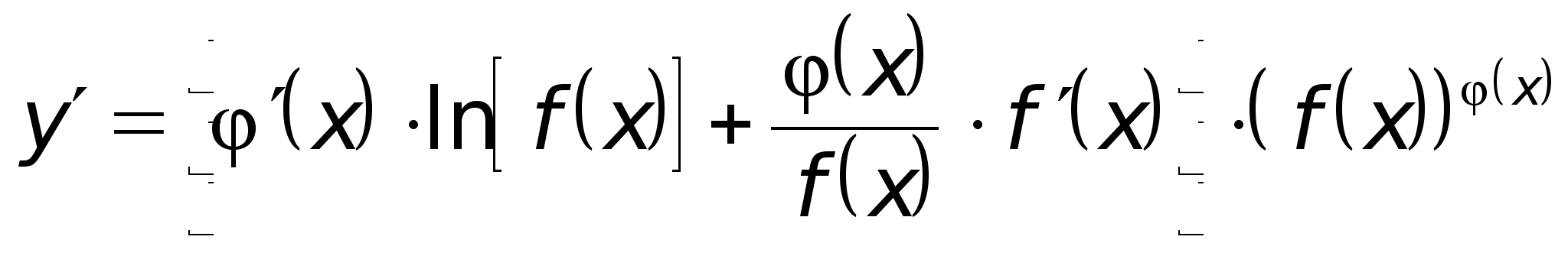 .
.
Логарифмическое
дифференцирование.
Пусть дана
функция
![]() .
При этом предполагается,
что функция
.
При этом предполагается,
что функция
![]() не обращается
в нуль в точке
не обращается
в нуль в точке
![]() .
Покажем один
из способов
нахождения
производной
функции
.
Покажем один
из способов
нахождения
производной
функции
![]() ,
если
,
если
![]() очень сложная
функция и по
обычным правилам
дифференцирования
найти производную
затруднительно.
очень сложная
функция и по
обычным правилам
дифференцирования
найти производную
затруднительно.
Так как по
первоначальному
предположению
![]() не равна нулю
в точке, где
ищется ее
производная,
то найдем новую
функцию
не равна нулю
в точке, где
ищется ее
производная,
то найдем новую
функцию
![]() и вычислим ее
производную
и вычислим ее
производную
![]() (1)
(1)
Отношение
![]() называется
логарифмической
производной
функции
называется
логарифмической
производной
функции
![]() .
Из формулы (1)
получаем
.
Из формулы (1)
получаем
![]() . Или
. Или
![]()
Формула
(2) дает простой
способ нахождения
производной
функции
![]() .
.
5. Производные высших порядков
Ясно,
что производная![]() функции
y =f (x) есть
также функция
от x:
функции
y =f (x) есть
также функция
от x:
![]()
Если
функция f
' (x)
дифференцируема,
то её производная
обозначается
символом y''
=f '' (x) и
называется
второй
производной
функции f(x) или
производной
функции f(x) второго
порядка.
Пользуясь
обозначением
![]() можем
написать
можем
написать
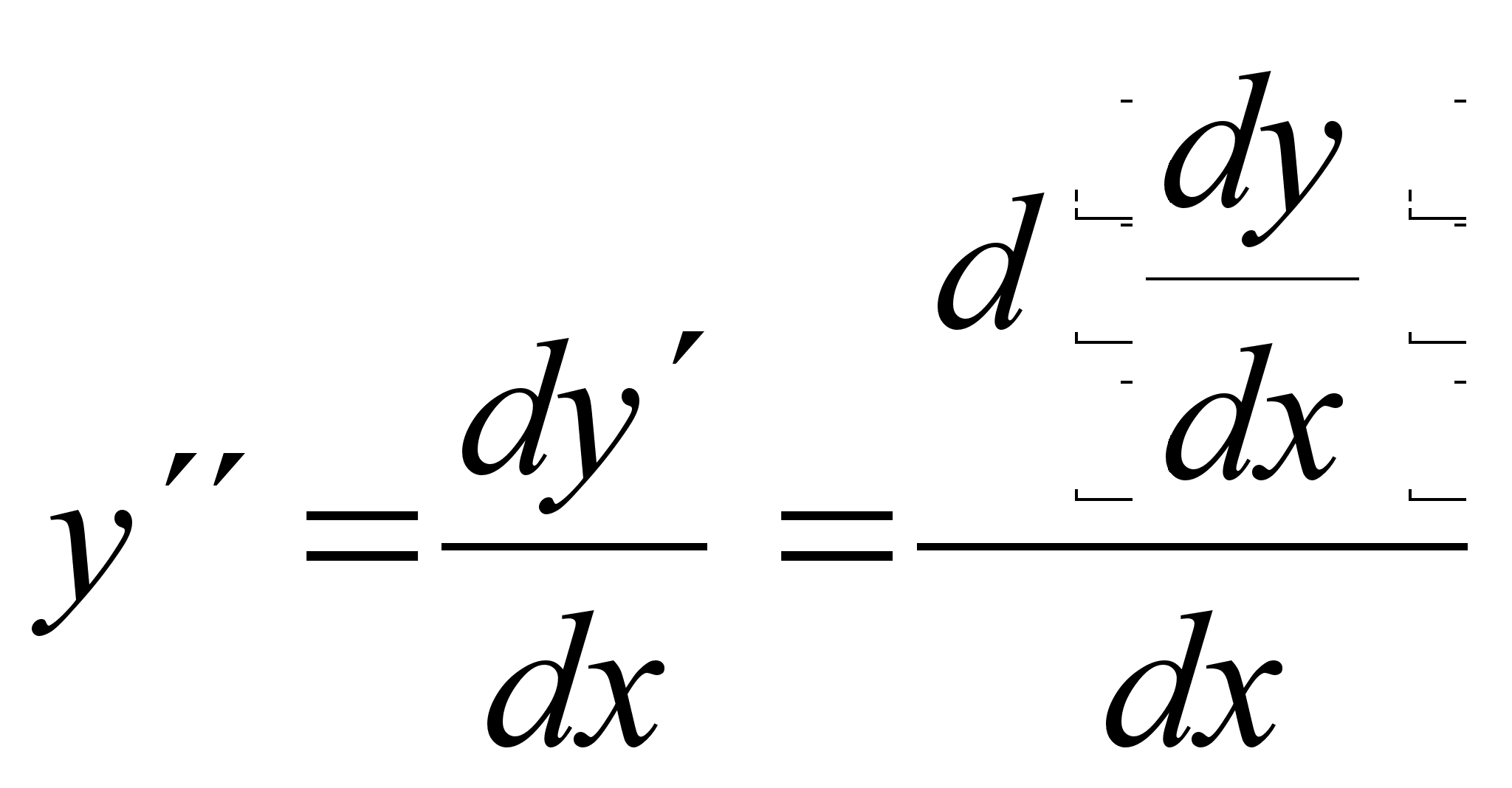
Очень
удобно пользоваться
также обозначением
![]() ,
указывающим,
что функция
y=f(x) была
продифференцирована
по x
два
раза.
,
указывающим,
что функция
y=f(x) была
продифференцирована
по x
два
раза.
Производная
второй производной,
т.е. функции
y''=f '' (x) ,
называется
третьей
производной
функции
y=f(x) или
производной
функции f(x) третьего
порядка
и обозначается
символами
![]() .
.
Вообще
n-я
производная
или производная
n-го
порядка функции
y=f(x)
обозначается
символами
![]()
Дифференцируя производную первого порядка, можно получить производную второго порядка, а, дифференцируя полученную функцию, получаем производную третьего порядка и т.д. Тогда возникает вопрос: сколько производных высших порядков можно получить в случае произвольной функции.
Например:
1)
![]() ;
;
![]() ;
;
![]() ;
...;
;
...;
![]() ;
;
![]() .
.
Разные функции ведут себя по-разному при многократном дифференцировании. Одни имеют конечное количество производных высших порядков, другие – переходят сами в себя, а третьи, хотя и дифференцируемы бесконечное количество раз, но порождают новые функции, отличные от исходной.
Однако все сформулированные теоремы о производных первых порядков выполняются для производных высших порядков.
6. Изучение функции с помощью производной
6.1.Возрастание и убывание функции. Экстремум функции.
Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если f(x2) > f(x1) при x2 > x1.
|
Рис.1 (а) |
|
Рис.1 (б) |
График возрастающей функции показан на рисунке1(а).
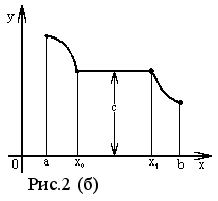
Если из неравенства x2 > x1 вытекает нестрогое неравенство f (x2) f (x1), то функция f (x) называется неубывающей в интервале (a, b ). Пример такой функции показан на рисунке 2(а). На интервале [ x0 , x1 ] она сохраняет постоянное значение C
Определение 2. Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x2) < f(x1) при x2 > x1.
Из
этого определения
следует, что
у убывающей
в интервале
( a, b )
функции
f (x)
в любой
точке этого
интервала
приращения
x
и
y
имеют
разные знаки. График
убывающей
функции показан
на рисунке
1(б).
Е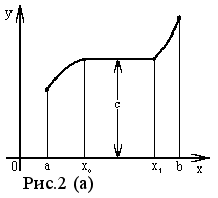 сли
из неравенства
x2
> x1
вытекает нестрогое
неравенство
f(x2) f(x1),
то функция
f (x)
называется
невозрастающей
в интервале
( a, b ).
Пример такой
функции показан
на рисунке
2(б). На интервале
[ x0
, x1
] она
сохраняет
постоянное
значение C.
сли
из неравенства
x2
> x1
вытекает нестрогое
неравенство
f(x2) f(x1),
то функция
f (x)
называется
невозрастающей
в интервале
( a, b ).
Пример такой
функции показан
на рисунке
2(б). На интервале
[ x0
, x1
] она
сохраняет
постоянное
значение C.
 Теорема
1.
Дифференцируемая
и возрастающая
в интервале
( a, b )
функция
f (x)
имеет
во всех точках
этого интервала
неотрицательную
производную.
Теорема
1.
Дифференцируемая
и возрастающая
в интервале
( a, b )
функция
f (x)
имеет
во всех точках
этого интервала
неотрицательную
производную.
Теорема
2.
Дифференцируемая
и убывающая
в интервале
( a, b )
функция
f (x)
имеет
во всех точках
этого интервала
неположительную
производную.
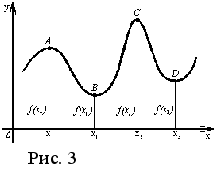
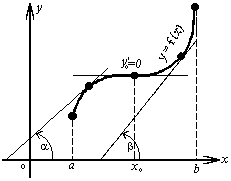
 Пусть
данная непрерывная
функция убывает
при возрастании
x от x0
до x1,
затем при возрастании
x от x1
до x2
- возрастает,
при дальнейшем
возрастании
x от x2
до x3
она вновь убывает
и так далее.
Назовем такую
функцию
колеблющейся.
Пусть
данная непрерывная
функция убывает
при возрастании
x от x0
до x1,
затем при возрастании
x от x1
до x2
- возрастает,
при дальнейшем
возрастании
x от x2
до x3
она вновь убывает
и так далее.
Назовем такую
функцию
колеблющейся.
График
колеблющейся
функции показан
на рисунке 3.
Точки A,
C, в
которых функция
переходит от
возрастания
к убыванию, так
же, как и точки
B, D,
в которых функция
переходит от
убывания к
возрастанию,
называются
точками
поворота
или критическими
точками кривой
y = f (x),
а их абциссы
- критическими
значениями
аргумента
x
В
той точке, где
функция переходит
от возрастания
к убыванию,
ордината больше
соседних с ней
по ту и другую
сторону ординат.
Так, ордината
точки A
больше ординат,
соседних с ней
справа и слева
и достаточно
к ней близких,
т.е. значение
функции в точке
A,
абсцисса которой
равна x0,
больше значений
функции в точках,
абсциссы которых
достаточно
близки к x0
: f (x0)
> f (x0+∆x).
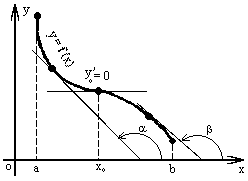
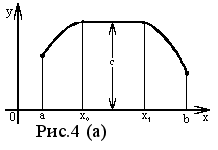
 На
рисунке 4(a) изображена
функция f
(x), непрерывная
в интервале
( a, b ).
В интервале
( a, x0 ]
она возрастает,
на интервале
[ x0 , x1 ]
- сохраняет
постоянное
значение: f
(x0)
= f (x1)
= C, в
интервале
[ x1 , b )
- убывает. Во
всех точках,
достаточно
близких к x0
(или x1
), значения функции
f (x)
удовлетворяют
нестрогому
неравенству
f (x0)f
(x).
На
рисунке 4(a) изображена
функция f
(x), непрерывная
в интервале
( a, b ).
В интервале
( a, x0 ]
она возрастает,
на интервале
[ x0 , x1 ]
- сохраняет
постоянное
значение: f
(x0)
= f (x1)
= C, в
интервале
[ x1 , b )
- убывает. Во
всех точках,
достаточно
близких к x0
(или x1
), значения функции
f (x)
удовлетворяют
нестрогому
неравенству
f (x0)f
(x).
Значение
f (x0)
функции f
(x), при
котором выполняется
вышеуказанное
неравенство,
называется
максимальным
значением
функции f
(x) или
просто максимумом.
Определение
3. Максимумом
функции
f (x)
называется
такое значение
f (x0)
этой функции,
которое не
меньше всех
значений функции
f (x)
в точках x,
достаточно
близких к точке
x0
, т.е. в точках
x,
принадлежащих
некоторой
достаточно
малой окрестности
точки x0
.
Так, на рисунке
3 показаны два
максимума: f
(x0)
и f (x2)
.
В той точке,
где функция
переходит от
убывания к
возрастанию,
ордината меньше
ординат в достаточно
близких к ней
точках, расположенных
справа и слева
от нее. Так ордината
точки B
меньше ординат
в точках соседних
и достаточно
близких к точке
x1
справа и слева.
Значение функции
в точке, абсцисса
которой равна
x1
, меньше значений
функции в точках,
абсциссы которых
достаточно
мало отличаются
от x1
: f (x1)
< f (x1+x).
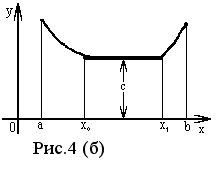
На рисунке 4(б) изображена функция f (x), непрерывная в интервале ( a, b ). В интервале ( a, x0 ] она убывает, на интервале [ x0 , x1 ] - сохраняет постоянное значение: f (x0) = f (x1) = C, в интервале [ x1 , b ) - возрастает. Во всех точках, достаточно близких к x0 (или x1 ), значения функции f (x) удовлетворяют нестрогому неравенству f (x0)f (x).
Значение
f (x0)
функции f
(x), при
котором выполняется
вышеуказанное
неравенство,
называется
минимальным
значением
функции f
(x) или
просто минимумом.
Определение
4. Минимумом
функции
f (x)
называется
такое значение
f (x0)
этой функции,
которое не
больше всех
значений функции
f (x)
в точках x,
достаточно
близких к точке
x0
, т.е. в точках
x,
принадлежащих
некоторой
достаточно
малой окрестности
точки x0
.
Так, на рисунке
3 показаны два
минимума: f
(x1)
и f (x3)
.
По определению
наибольшим
значением
функции f
(x) на
интервале
[ a, b ]
является такое
значение f
(x0),
для которого
для всех точек
интервала
[ a, b ]
выполняется
неравенство
f (x0)f
(x), а
наименьшим
значением
функции f
(x) на
интервале
[ a, b ]
является такое
значение f
(x0),
для которого
для всех точек
интервала
[ a, b ]
выполняется
неравенство
f (x0)f
(x).
Из
этих определений
следует, что
функция может
достигать
своего наибольшего
или наименьшего
значения как
внутри интервала
[ a, b ]
, так и на его
концах a
и b.
Здесь же максимум
и минимум функции
f (x)
были определены
соответственно
как наибольшее
и наименьшее
значения в
некоторой
окрестности
точки x0
.
Если в точке
x0
функция f
(x) достигает
максимума или
минимума, то
говорят, что
функция f
(x) в
точке x0
достигает
экстремума
(или экстремального
значения).
Функция
f (x)
может иметь
несколько
экстремумов
внутри интервала
[ a, b ],
причем может
оказаться, что
какой-нибудь
минимум будет
больше какого-нибудь
максимума.
Таким образом,
наибольшее
значение функции
f (x) на интервале
[ a, b ] - это наибольший
из экстремумов
функции внутри
этого интервала
и наибольшее
из значений
функции на
концах интервала.
Аналогично
наименьшее
значение функции
f (x) на интервале
[ a, b ] - это наименьший
из экстремумов
функции внутри
этого интервала
и наименьшее
из значений
функции на
концах интервала.
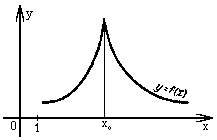
Например функция, изображенная на рисунке 3, достигает наибольшего значения f (x) в точке x2 , наименьшего - в точке x1 интервала [ x0, x3 ]. На рисунке 5 изображена функция, имеющая бесконечное число минимумов и максимумов.
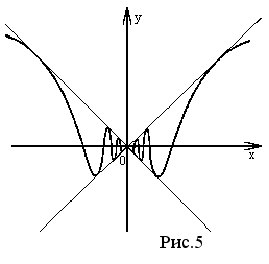 Теорема
3 (необходимый
признак экстремума).
Если функция
f (x) имеет в точке
x0
экстремум, то
ее производная
в данной точке
или равна нулю
или не существует.
Теорема
3 (необходимый
признак экстремума).
Если функция
f (x) имеет в точке
x0
экстремум, то
ее производная
в данной точке
или равна нулю
или не существует.
Но
функция f
(x) может
иметь экстремумы
и в тех точках
x0,
в которых ее
производная
не существует.
Например функция
y = |
x | в
точке x0
= 0 не
дифференцируема,
но достигает
минимума. Точки
такого типа
называют угловыми.
В них кривая
не имеет определенной
касательной.
|
Рис. 6 |
Таким образом, необходимым признаком существования в точке x0 экстремума функции f (x) является выполнение следующего условия: в точке x0 производная f' (x) или равна нулю, или не существует.
Этот признак не является достаточным условием существования экстремума функции f (x) в точке x0 : можно привести много примеров функций, удовлетворяющих этому условию при x = x0 , но, однако, не достигающих экстремума при x = x0.
Например, производная функции y = x3 при x0 = 0 равна нулю, однако эта функция при x0 = 0 не достигает экстремального значения.
6.2.Достаточные условия убывания и возрастания функции. Достаточные условия экстремума функции.
Теорема
4.Если
функция f(x) имеет
в каждой точке
интервала
(a, b) неотрицательную
производную,
то она является
неубывающей
функцией в
этом интервале.
Теорема
5. Если
функция f(x) в
каждой точке
интервала
(a, b) имеет неположительную
производную,
то она является
невозрастающей
функцией в
этом интервале.
Теорема
6. (первый
достаточный
признак экстремума).
Если
производная
f '(x) функции f(x)
обращается
в нуль в точке
x0
или не существует
и при переходе
через x0
меняет свой
знак, то функция
f(x) имеет в этой
точке экстремум
(максимум, если
знак меняется
с "+" на "-", и минимум,
если знак меняется
с "-" на "+").
Теорема
7. (второй
достаточный
признак существования
экстремума
функции). Если
в точке x0
первая производная
f '(x) функции f(x)
обращается
в нуль, а её вторая
производная
f ''(x) отлична от
нуля, то в точке
x0
функция f(x) достигает
экстремума
(минимума, если
f ''(x) > 0, и максимума,
если f ''(x) < 0).
Предполагается,
что f ''(x) непрерывна
в точке x0
и ее окрестности.
6.3 .Правило нахождения экстремума
1°. Чтобы найти экстремум функции, надо:
1) найти производную данной функции;
2) приравнять производную нулю и решить полученное уравнение; из полученных корней отобрать действительные и расположить их (для удобства) по их величине от меньшего к большему; в том случае, когда все корни оказываются мнимыми, данная функция не имеет экстремума;
3) определить знак производной в каждом из промежутков, отграниченных стационарными точками ( стационарными точками называют точки в которых производная равна 0);
4) если производная положительна в промежутке, лежащем слева от данной стационарной точки, и отрицательна в промежутке, лежащем справа от нес, то данная точка есть точка максимума функции, если же производная отрицательна слева и положительна справа от данной стационарной точки, то данная точка есть точка минимума функции; если производная имеет один и тот же знак как слева, так и справа от стационарной тонки, то в этой точке нет ни максимума, ни минимума, функции;
5) заменить в данном выражении функции аргумент значением, которое дает максимум или минимум функции; получим значение соответственно максимума или минимума функции.
Если функция имеет точки разрыва, то эти точки должны быть включены в число стационарных точек, разбивающих Ох на промежутки, в которых определяется знак производной.
6.4.Точка перегиба графика функции.
Будем говорить, что кривая y = f(x) в точке x0 обращена выпуклостью вверх, если существует такая окрестность точки x0 , что часть кривой, соответствующая этой окрестности, лежит под касательной к этой кривой, проведенной в точке A с абсциссой x0. (см. Рисунок 1а).
|
Р а
б исунок 1 |
Из определения выпуклости вверх (вниз) кривой y = f(x) в точке x0 следует, что для любой точки x из интервала (x0 - h, x0 + h), не совпадающей с точкой x0, имеет место неравенство f(x) - y < 0 ( f(x) - y > 0) где f(x) - ордината точки M кривой y = f(x), y - ордината точки N касательной y - y0 = f '(x0 )(x - x0 ) к данной кривой в точке A. (смотри рисунок 1, а, б).
Ясно, что и наоборот, если для любой точки x интервала (x0 - h, x0 + h), не совпадающей с x0, выполняется неравенство f(x) - y < 0 (f(x) - y > 0),
то
кривая y = f(x)
в точке x0
обращена выпуклостью
вверх (вниз).
Будем
называть кривую
y = f(x)
выпуклой
вверх (вниз)
в интервале
(a, b),
если она выпукла
вверх (вниз) в
каждой точке
этого интервала.
Если
кривая y = f(x)
обращена выпуклостью
вверх в интервале
(a, b),
то с увеличением
аргумента x
угловой коэффициент
касательной
к этой кривой
в точке с абсциссой
x
будет уменьшаться.
|
Рисунок 2. |
Таким образом мы показали, что если в интервале (a, b) кривая y = f(x) обращена выпуклостью вверх, то с увеличением аргумента x функция y = f '(x) убывает. Поэтому вторая производная f ''(x) функции f(x), как производная убывающей фунции f '(x), будет отрицательна или равна нулю в интервале (a, b): f ''(x)0.
|
Рисунок 3. |
Докажем, что и наоборот, если f ''(x)0 в некотором интервале (a, b), то в этом интервале кривая y = f (x) обращена выпуклостью вверх; если f ''(x)0 в интервале (a, b), то в этом интервале кривая обращена выпуклостью вниз.
Запишем уравнение касательной y - y0 = f '(x0 )(x - x0 ) к кривой y = f (x) в точке x0, где a < x0 b, в виде y = y0 + f '(x0 )(x - x0 ). Очевидно, y0 = f(x0 ), а потому последнее уравнение можно записать в виде y = f(x0 ) + f '(x0 )(x - x0 ). (1)
Но, согласно формуле Тейлора, при n = 2 имеем:
![]() (2)
(2)
Фиксируя
x
в интервале
(a, b)
и вычитая почленно
из уравнения
(2) уравнение
(1), получим:![]() (3)
(3)
Если f ''[x0 + (x - x0 )]0, где 0 < < 1, то имеем f(x) - y 0
откуда
следует, что
кривая y = f(x)
в точке x
обращена выпуклостью
вверх.
Если
f ''[x0 + (x - x0 )]0,
то имеем f(x) - y 0
откуда следует,
что кривая
y = f(x)
в точке x
обращена выпуклостью
вниз.
Так
как была зафиксирована
произвольная
точка x
интервала
(a, b),
то высказанное
выше утверждение
доказано.
|
Рисунок 4. |
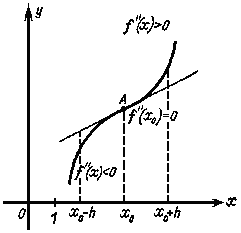
Теорема 8. Пусть функция f(x) имеет непрерывную вторую производную f ''(x) и пусть A[x0 ; f(x0 )] - точка перегиба кривой y = f(x). Тогда f ''(x0 ) = 0 или не существует.
Доказательство. Рассмотрим для определенности случай, когда кривая y = f(x) в точке перегиба A[x0 ; f(x0 )] переходит от выпуклости вверх в выпуклости вниз (рис.4). Тогда при достаточно малом h в интервале (x0 - h, x0 ) вторая производная f ''(x) будет меньше нуля, а в инетрвале (x0, x0 +h) - больше нуля.
Но f ''(x) - функция непрерывная, а потому, переходя от отрицательных значений к положительным, она при x = x0 обращается в нуль: f ''(x0 ) = 0.
|
Рисунок 5. |
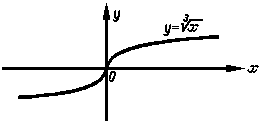
Итак,
f ''(0)
не существует.
Но тем не менее
точка O(0; 0)
является точкой
перегиба, так
как при x < 0 f ''(x) > 0
и кривая выпукла
вниз, а при
x > 0 f ''(x) < 0
и кривая выпукла
вверх.
Таким
образом в случае
непрерывности
второй производной
f ''(x)
обращение в
нуль или несуществование
ее в какой-нибудь
точки кривой
y = f(x)
является необходимым
условием
существования
точки перегиба.
Однако это
условие не
является
достаточным.
Теорема
9. Если
вторая производная
f ''(x)
непрерывна
и меняет знак
при
x = x0,
то
точка
A[x0 ;
f(x0 )]
является
точкой перегиба
кривой
y = f(x)
при
условии, конечно,
что в точке
A
существует
касательная.
Доказательство.
Пусть например
f ''(x) < 0
при x0 - h < x < x0
и f ''(x) > 0
при x0 < x < x0 + h.
Тогда в интервале
(x0 - h; x0 )
кривая y = f(x)
обращена выпуклостью
вверх, а в интервале
(x0 ; x0 + h)
- выпклостью
вниз (смотри
рис.4), т.е. точка
A[x0 ;
f(x0 )]
есть точка
перегиба кривой,
что и требовалось
доказать.
6.5.Общая схема исследования функции и построение ее графика.
1.
Находим область
определения
функции f(x)
2.
Находим точки
пересечения
кривой y = f(x)
с осями координат
и наносим их
на чертеж.
3.
Определяем,
симметрична
ли кривая y = f(x)
относительно
осей координат
и начала координат.
4.
Исследуем
функцию y = f(x)
на непрерывность.
Если функция
имеет в точке
x0
разрыв, то отмечаем
ее на чертеже.
5.
Находим асимптоты
кривой, если
они имеются.
6.
Находим максимум
и минимум функции
и отмечаем на
чертеже точки
кривой с максимальной
и минимальной
ординатами.
7.
Исследуем
кривую y = f(x)
на выпуклость
вверх или вниз,
находим точки
перегиба кривой
и отмечаем их
на чертеже.
8.
Вычерчиваем
кривую y = f(x).
6.6. Касательная и нормаль к плоской кривой.
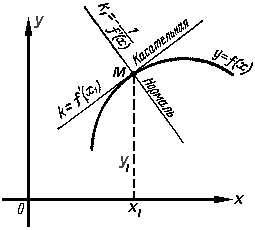 Пусть
даны кривая
y = f(x)
и точка M (x1 ; y1)
на ней. Требуется
составить
уравнения
касательной
и нормали (смотри
рисунок).
Пусть
даны кривая
y = f(x)
и точка M (x1 ; y1)
на ней. Требуется
составить
уравнения
касательной
и нормали (смотри
рисунок).
Как
известно, угловой
коэффициент
k
касательной
к кривой y = f(x)
в точке M (x1 ; y1)
равен значению
f '(x1)
производной
y' = f '(x)
при x = x1/
Следовательно,
уравнение
касательной
можно записать
в виде уравнения
прямой, проходящей
через данную
точку в данном
направлении,
т.е. в виде
y - y1 = f '(x1)(x - x1)
Нормалью
называется
прямая, проходящая
через точку
касания перпендикулярно
касательной.
поэтому ее
угловой коэффициент
равен
![]() ,
а уравнение
записывается
в виде
,
а уравнение
записывается
в виде
![]()
7.Экономическое приложение производной.
7.1.Экономическая интерпретация производной
В экономической теории активно используется понятие «маржинальный», что означает «предельный». Введение этого понятия в научный оборот в XIX веке позволило создать совершенно новый инструмент исследования и описания экономических явлений - инструмент, посредством которого стало возможно ставить и решать новый класс научных проблем.
Классическая экономическая теория Смита, Рикардо, Милля обычно имела дело со средними величинами: средняя цена, средняя производительность труда и т.д. Но постепенно сложился иной подход. Существенные закономерности оказалось можно обнаружить в области предельных величин.
Предельные или пограничные величины характеризуют не состояние (как суммарная или средняя величины.), а процесс, изменение экономического объекта. Следовательно, производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.
Надо заметить, что экономика не всегда позволяет использовать предельные величины в силу прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). В то же время во многих случаях можно отвлечься от дискретности и эффективно использовать предельные величины.
Рассмотрим ситуацию: пусть y - издержки производства, а х - количество продукции, тогда x- прирост продукции, а y - приращение издержек производства.
В этом случае
производная
![]() выражает предельные
издержки
производства
и характеризует
приближенно
дополнительные
затраты на
производство
дополнительной
единицы продукции
выражает предельные
издержки
производства
и характеризует
приближенно
дополнительные
затраты на
производство
дополнительной
единицы продукции
![]() ,где
MC – предельные
издержки (marginal
costs); TC – общие издержки
(total costs); Q - количество.
,где
MC – предельные
издержки (marginal
costs); TC – общие издержки
(total costs); Q - количество.
Г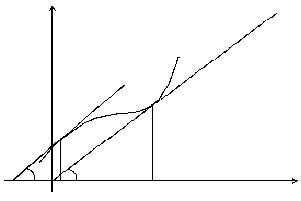
С
С
C(t)
еометрическая интерпретация предельных издержек - это тангенс угла наклона касательной к кривой в данной точке (см. рис.).А
E
A
налогичным образом могут быть определены и многие другие экономические величины, имеющие предельный характер.Д
![]()
![]()
Q
B
ругой пример - категория предельной выручки (MR— marginal revenue) — это дополнительный доход, полученный при переходе от производства n-ной к (n+1)-ой единице продукта.Она
представляет
собой первую
производную
от выручки:
![]() .
.
При этом R= PQ, где R–выручка (revenue); P–цена (price).
Таким
образом
![]() ,
MR= P.
,
MR= P.
Это равенство верно относительно условий совершенной конкуренции, когда экономические агенты каждый по отдельности не могут оказать влияния на цену.
Обратимся к теориям потребления: кардиналистской и ординалистской.
Кардиналистский (количественный) подход к теории цен предполагает равное влияние величин полезности товара и затрат на его производства на формирование цены. В основе рассматриваемого подхода - исследования А. Маршалла.
Ординалистский (Порядковый) подход к теории цен разрабатывался И. Фишером, В. Парето. Суть данного подхода состоит в том, что потребители, имеющие определенный уровень доходов, сравнивают между собой цены и полезность различных наборов экономических благ и отдают предпочтение тем наборам, которые при сравнительно низких ценах имеют максимальную полезность для конкретного потребителя.
В соответствии с первой, суммарную полезность U для любого субъекта, если в экономике существует n потребительских благ в объемах х1, x2,… хn, можно выразить в виде кардиналистской функции полезности:
U= U(х1, x2,… xn).
Предельные
полезности
MU товаров
выступают в
качестве ее
частных производных:
![]() .
Они показывают,
на сколько
изменяется
полезность
всей массы
благ, достающихся
субъекту, при
бесконечно
малом приращении
количества
блага i
(i=1,2…n)
.
Они показывают,
на сколько
изменяется
полезность
всей массы
благ, достающихся
субъекту, при
бесконечно
малом приращении
количества
блага i
(i=1,2…n)
В ординалистской теории полагается, что потребитель оценивает полезность не отдельных благ, а потребительских наборов; что он способен сопоставить полезности наборов товаров.
Ординалистская функция полезности исследована подробно, значительный вклад в ее изучение внес Дж. Хикс. После его трудов началось прогрессирующее вытеснение понятия "предельная полезность" категорией предельной нормы замещения (MRS – marginal rate of substitution).
Предположим, что происходит замещение товара y товаром х при движении сверху вниз вдоль кривой безразличия. Предельная норма замещения товара y товаром x показывает, какое количество товара x необходимо для того, чтобы компенсировать потребительскую утрату единицы товара y.
Они
определяются
так: ![]() .
.
Т.к. dy отрицательно, знак "-" вводится, чтобы MRS была больше нуля.
Итак, предельная норма замещения геометрически есть касательная к кривой безразличия в данной точке. Значение предельной нормы замещения по абсолютной величине равно тангенсу угла наклона касательной к кривой безразличия.
Приведем еще один пример элементарного анализа на микроуровне, который имеет аналог и на макроуровне.
Любой индивид свой доход Y после уплаты налогов использует на потребление C и сбережение S. Ясно, что лица с низким доходом, как правило, целиком используют его на потребление, так что размер сбережения равен нулю. С ростом дохода субъект не только больше потребляет, но и больше сберегает. Как установлено теорией и подтверждено эмпирическими исследования, потребление и сбережение зависят от размера дохода:
Y= C(Y) + S(Y).
Зависимость потребления индивида от дохода называется функцией склонности к потреблению или функцией потребления.
Использование
производной
позволяет
определить
такую категорию,
как предельную
склонность
к потреблению
MPC (marginal property to consume), показывающую
долю прироста
личного потребления
в приросте
дохода:
![]() .
.
По мере увеличения
доходов MPC
уменьшается.
Последовательно
определяя
сбережения
при каждом
значении дохода,
можно построить
функцию склонности
к сбережению
или функцию
сбережения. Долю
прироста сбережений
в приросте
дохода показывает
предельная
склонность
к сбережению
MPS(marginal propensity to save): ![]() .
.
С увеличением доходов MPS увеличивается.
Еще одним
примером
использования
производной
в экономике
является анализ
производственной
функции. Поскольку
ограниченность
ресурсов
принципиально
не устранима,
то решающее
значение приобретает
отдача от факторов
производства.
Здесь также
применима
производная,
как инструмент
исследования.
Пусть применяемый
капитал постоянен,
а затраты труда
увеличиваются.
Можно ввести
в экономический
анализ следующую
категорию -
предельный
продукт труда
MPL(marginal
product of labor) – это дополнительный
продукт, полученный
в результате
дополнительных
вложений труда
(L – labor) при неизменной
величине капитала:![]() .
.
Если
вложения
осуществляются
достаточно
малыми порциями,
то
![]() ,
т.к. dY - результат,
dL - затраты, то
MPL –
предельная
производительность
труда.
,
т.к. dY - результат,
dL - затраты, то
MPL –
предельная
производительность
труда.
Аналогично,
MPk
- предельный
продукт капитала
- дополнительный
продукт, полученный
в результате
дополнительных
вложений капитала
K при
неизменной
величине труда:![]() .
.
Если вложения
осуществляются
малыми порциями,
то
![]() .
.
MPk - характеризует предельную производительность капитала.
Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции.
Определение: Эластичностью функции Еx(y) называется предел отношения относительного приращения функции y к относительному приращению переменной x при x0:
![]() .
.
Эластичность функции показывает приближенно, на сколько процентов изменится функция y= f(x), при изменении независимой переменной x на 1%.
Приведем
несколько
конкретных
иллюстраций
такой зависимости.
Прямой коэффициент
эластичности
спроса по цене
устанавливает,
на сколько
процентов
увеличивается
(уменьшается)
спрос Q на
товар i при
уменьшении
(увеличении)
его цены P
на 1%: ![]() .
.
Перекрестный
коэффициент
эластичности
спроса по цене
![]() показывает,
на сколько
процентов
изменится
спрос на товар
i при
однопроцентных
колебаниях
цены товара
j (j = 1,2,…n):
показывает,
на сколько
процентов
изменится
спрос на товар
i при
однопроцентных
колебаниях
цены товара
j (j = 1,2,…n): ![]() .
.
Количественную
сторону взаимодействия
дохода и спроса
отражает коэффициент
эластичности
спроса по доходу,
который указывает,
на сколько
процентов
изменится
спрос на i-тый
товар Qi
если доход,
предназначенный
на текущее
потребление,
изменится на
1%: ![]() .
.
Можно привести и другие примеры использования производной при фокусировке различных категорий и закономерностей. Дальнейшее раскрытие экономического смысла хотелось бы осуществить через рассмотрение экономической интерпретации математических теорем.
7.2. Применение производной в экономической теории.
Проанализировав экономический смысл производной, нетрудно заметить, что многие, в том числе базовых законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем.
Вначале рассмотрим экономическую интерпретацию теоремы: если дифференцируемая на промежутке X функция y= f(x) достигает наибольшего или наименьшего значения во внутренней точке x0 этого промежутка, то производная функции в этой точке равна нулю, то есть f’(x0) = 0.
Один из базовых законов теории производства звучит так: "Оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода".
То есть уровень выпуска Qo является оптимальным для производителя, если MC(Qo)=MR(Qo), где MC - предельные издержки, а MR - предельный доход.
Обозначим функцию прибыли за П(Q). Тогда П(Q) = R(Q) — C(Q), где R – прибыль, а C – общие издержки производства.
Очевидно, что оптимальным уровнем производства является тот, при котором прибыль максимальна, то есть такое значение выпуска Qo, при котором функция П(Q) имеет экстремум (максимум). По теореме Ферма в этой точке П’(Q) = 0. Но П’(Q)=R’(Q) - C’(Q), поэтому R’(Qo) = C’(Qo), откуда следует, что MR(Qo) = MC(Qo).
Другое важное понятие теории производства - это уровень наиболее экономичного производства, при котором средние издержки по производству товара минимальны. Соответствующий экономический закон гласит: “оптимальный объем производства определяется равенством средних и предельных издержек”.
Получим
это условие
как следствие
сформулированной
выше теоремы.
Средние издержки
AC(Q) определяются
как
![]() ,
т.е. издержки
по производству
всего товара,
деленные на
произведенное
его количество.
Минимум этой
величины достигается
в критической
точке функции
y=AC(Q), т.е.
при условии
,
т.е. издержки
по производству
всего товара,
деленные на
произведенное
его количество.
Минимум этой
величины достигается
в критической
точке функции
y=AC(Q), т.е.
при условии
![]() ,
откуда TC’(Q)Q—TC(Q)
= 0 или
,
откуда TC’(Q)Q—TC(Q)
= 0 или
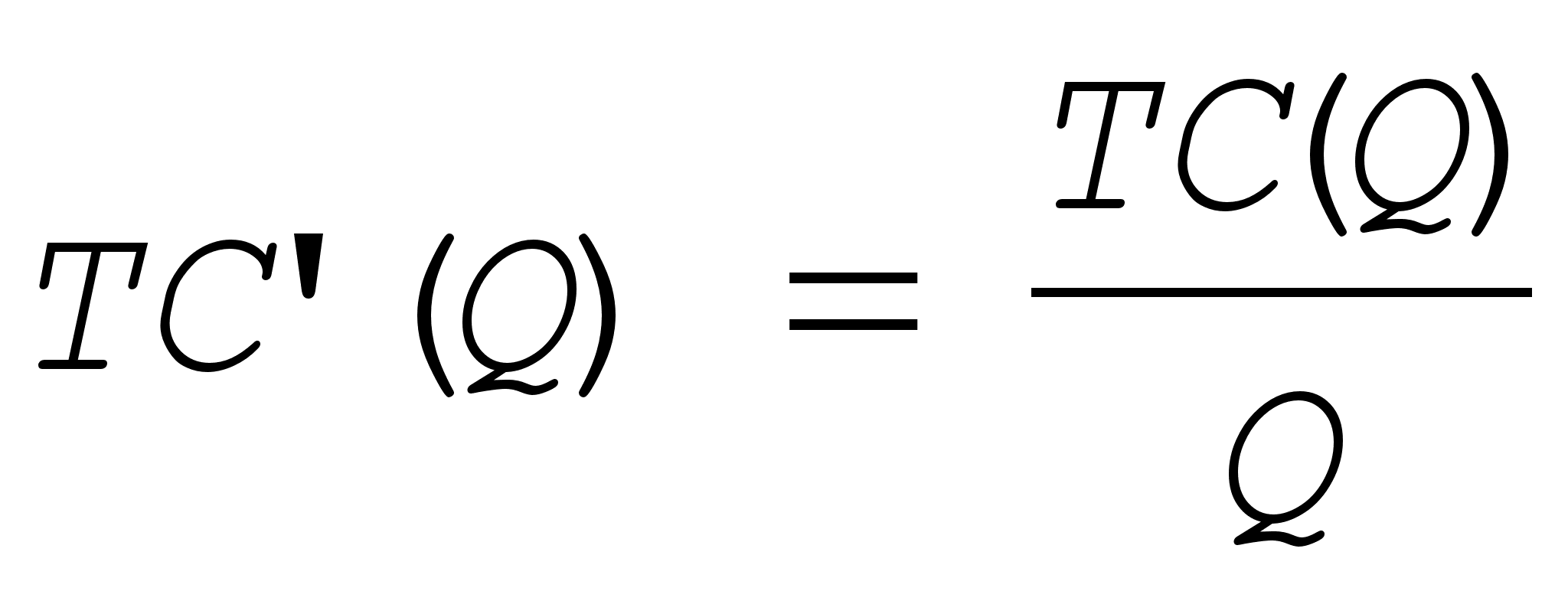 ,
т.е. MC(Q)=AC(Q).
,
т.е. MC(Q)=AC(Q).
Понятие выпуклости функции также находит свою интерпретацию в экономической теории.
Один из наиболее знаменитых экономических законов - закон убывающей доходности - звучит следующим образом: "с увеличением производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и т.д.), с некоторого момента убывает".
Иными словами,
величина
![]() ,
где y
- приращение
выпуска продукции,
а x
- приращение
ресурса, уменьшается
при увеличении
x. Таким
образом, закон
убывающей
доходности
формулируется
так: функция
y= f(x), выражающая
зависимость
выпуска продукции
от вложенного
ресурса, является
функцией, выпуклой
вверх.
,
где y
- приращение
выпуска продукции,
а x
- приращение
ресурса, уменьшается
при увеличении
x. Таким
образом, закон
убывающей
доходности
формулируется
так: функция
y= f(x), выражающая
зависимость
выпуска продукции
от вложенного
ресурса, является
функцией, выпуклой
вверх.
Другим базисным понятием экономической теории является функция полезности U= U(x), где х - товар, а U – полезность (utility). Эта величина очень субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Закон убывающей полезности звучит следующим образом: с ростом количества товара, дополнительная полезность от каждой новой его единицы с некоторого момента убывает. Очевидно, этот закон можно переформулировать так: функция полезности является функцией, выпуклой вверх. В такой постановке закон убывающей полезности служит отправной точкой для математического исследования теории спроса и предложения.
7.3. Использование производной для решения задач по экономической теории.
Задача 1.
Цементный завод производит Х т. цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т. цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90 т. в день.
Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид:
К=-х3+98х2+200х. Удельные затраты составят К/х=-х2+98х+200
Наша задача сводится к отысканию наибольшего и наименьшего значения функции У= -х2+98х+200. На промежутке [20;90].
Вывод: x=49, критическая точка функции. Вычисляем значение функции на концах промежутках и в критической точке.
f(20)=1760 f(49)=2601 f(90)=320.
Таким образом, при выпуске 49 тонн цемента в день удельные издержки максимальны, это экономически не выгодно, а при выпуске 90 тонн в день минимально, следовательно можно посоветовать работать заводу на предельной мощности и находить возможности усовершенствовать технологию, так как дальше будет действовать закон убывающей доходности. И без реконструкции нельзя будет увеличить выпуск продукции.
Задача 2.
Задача: Предприятие производит Х единиц некоторой однородной продукции в месяц. Установлено, что зависимость финансовых накопления предприятия от объема выпуска выражается формулой f(x)=-0,02x^3+600x -1000. Исследовать потенциал предприятия.
Функция исследуется с помощью производной. Получаем, что при Х=100 функция достигает максимума.
Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при х =100 они достигают максимума и объем накопления равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению финансовых накоплений.
Задача 3.
Спрос-это зависимость между ценой единицы товара и количеством товара, которое потребители готовы купить при каждой возможной цене, за определенный период времени и при прочих равных условиях.
Зависимость
спроса от цены
описывается
функцией
![]() ,
,
Данная
функция исследуется
с помощью
производной:
![]()
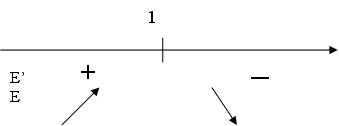
Производная меньше нуля, если P>=0.
Определим точку перегиба функции. Такой точкой является точка (0,5;0,6), т.е. при P1/2 спрос убывает все быстрее.
Задача 4.
Выручка
от реализации
товара по цене
p составляет:
![]()
(Денежных
единиц), где
![]() .
Исследуем эту
функцию с помощью
производной.
.
Исследуем эту
функцию с помощью
производной.
Производная
этой функции:
![]() положительна,
если p1/2, это означает,
что с ростом
цены выручка
в начале увеличивается
( несмотря на
падение спроса)
и p=1/2 достигает
максимального
значения
положительна,
если p1/2, это означает,
что с ростом
цены выручка
в начале увеличивается
( несмотря на
падение спроса)
и p=1/2 достигает
максимального
значения
![]() ,
дальнейшее
увеличение
цены не имеет
смысла, т.как
оно ведет к
сокращению
выручки. Темп
изменения
выручки выражается
второй производной.
,
дальнейшее
увеличение
цены не имеет
смысла, т.как
оно ведет к
сокращению
выручки. Темп
изменения
выручки выражается
второй производной.
![]()
![]() темп
положительный
темп
положительный
![]() темп
отрицательный
темп
отрицательный
На
промежутке
(0,1/2) функция возрастает
все медленнее,
то есть дальнейшее
повышение цены
не выгодно.
Сначала выручка
убывает с
отрицательным
темпом для
![]() ,
а затем темп
убывания становится
положительным
и для P>0,9 выручка
убывает все
быстрее и
приближается
к нулю при
неограниченном
увеличении
цены.
,
а затем темп
убывания становится
положительным
и для P>0,9 выручка
убывает все
быстрее и
приближается
к нулю при
неограниченном
увеличении
цены.
Для наглядной демонстрации выше сказанного составим таблицу и построим график.
| p | (0, 1/2) | 1/2 |
|
|
|
| U'(p) | + | 0 | - | -0,47 | - |
| U''(p) | - | - | 0 | + | |
| U (p) |
возрастает выпукла |
0,3 max |
убывает выпукла |
0,2 точка перегиба |
убывает вогнута |
Вывод:
На промежутке (0, 1/2) функция возрастает все медленнее.
Соответствующая
часть графика
выпукла. Как
уже отмечалось,
дальнейшее
повышение цены
не выгодно.
Сначала выручка
убывает с
отрицательным
темпом![]() ,
а затем темп
убывания V(p)
становится
положительным.
Для р > 0,9 выручка
убывает все
быстрее и
приближается
к нулю при
неограниченном
увеличении
цены. На промежутке
,
а затем темп
убывания V(p)
становится
положительным.
Для р > 0,9 выручка
убывает все
быстрее и
приближается
к нулю при
неограниченном
увеличении
цены. На промежутке
![]() функция
U(p) вогнута. В
точке
функция
U(p) вогнута. В
точке
![]() график
перегибается
(см. на рисунке):
график
перегибается
(см. на рисунке):
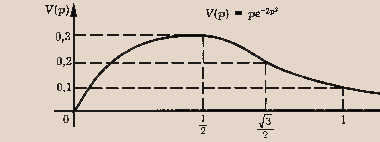
![]()
![]()
![]()
8. Применение производной в физике
В физике производная применяется в основном для вычисления наибольших или наименьших значений для каких-либо величин.
Задача 1.
Лестница длиной 5м приставлена к стене таким образом, что верхний ее конец находится на высоте 4м. В некоторый момент времени лестница начинает падать, при этом верхний конец приближается к поверхности земли с постоянным ускорением 2 м/с2. С какой скоростью удаляется от стены нижний конец лестницы в тот момент, когда верхний конец находится на высоте 2м?
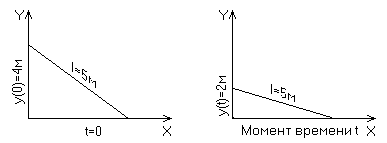
Пусть верхний конец лестницы в момент времени t находится на высоте y(0)= 4м, а нижний на расстоянии x(t) от стенки.
Высота
y(t)
описывается
формулой:
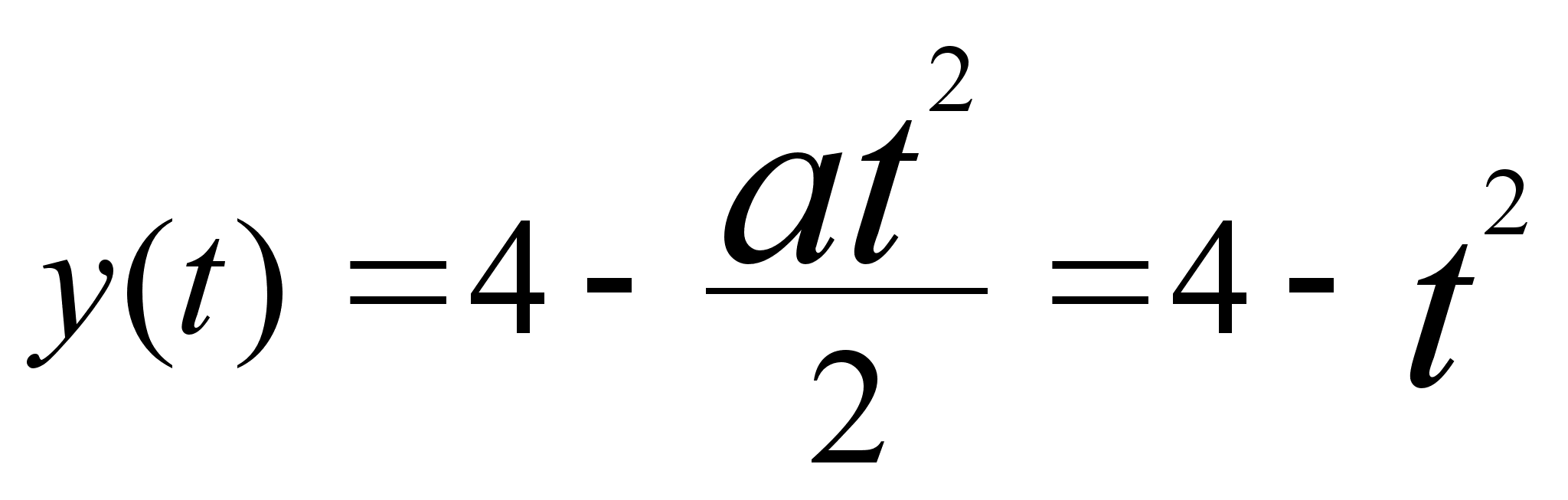 ,так
как движение
равноускоренное.
,так
как движение
равноускоренное.
В
момент t:
y(t)
= 2, т.е. 2 = 4 - t2,
из
которого
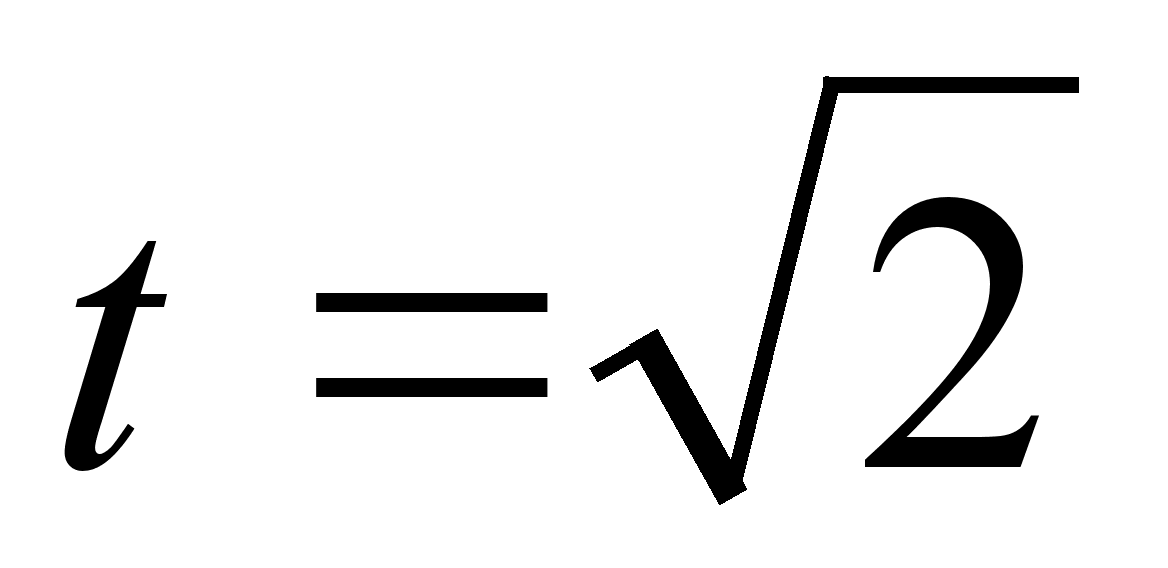 ;
;
В
этот
момент
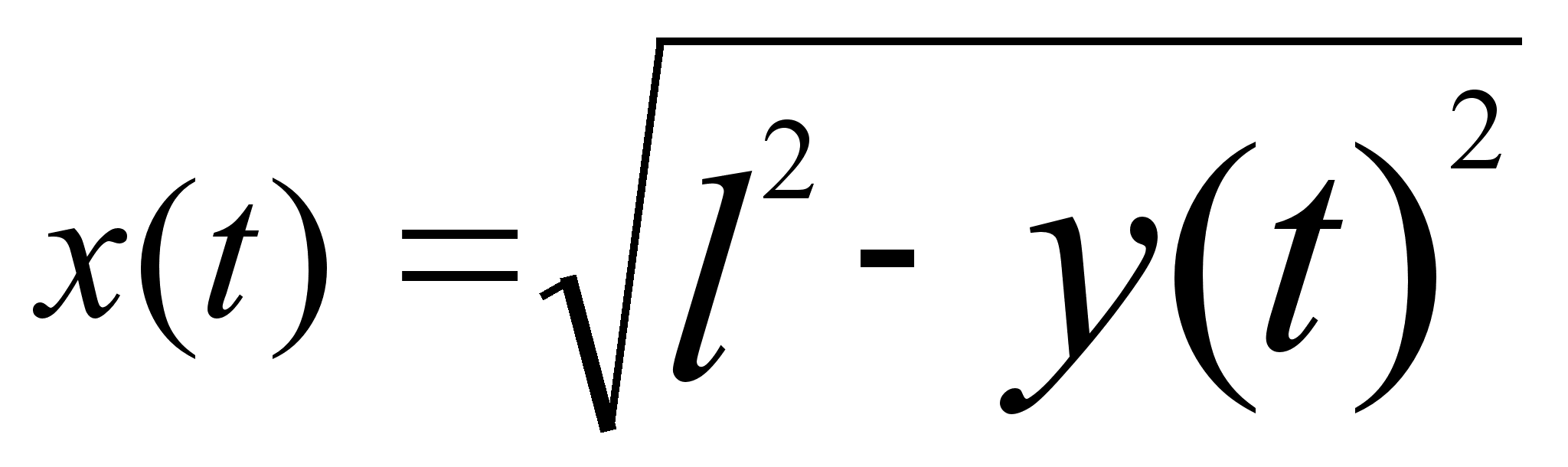 по т. Пифагора,
т.е.
по т. Пифагора,
т.е.
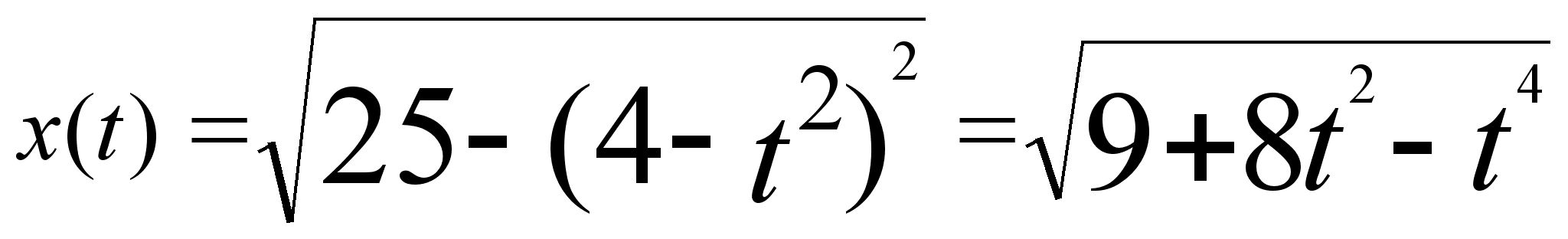
Скорость
его изменения
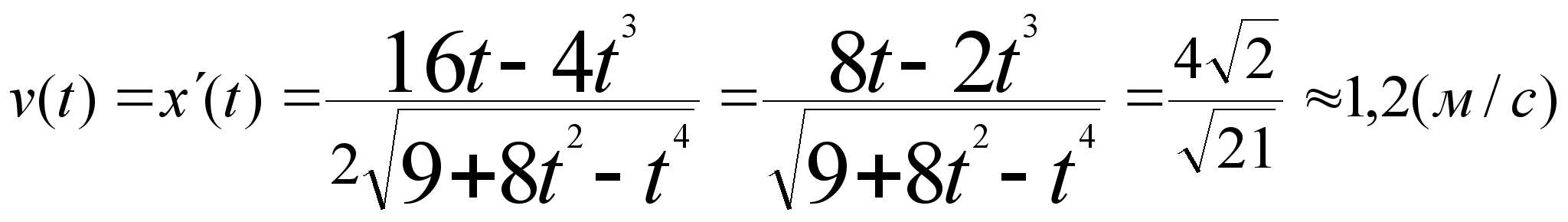
Ответ: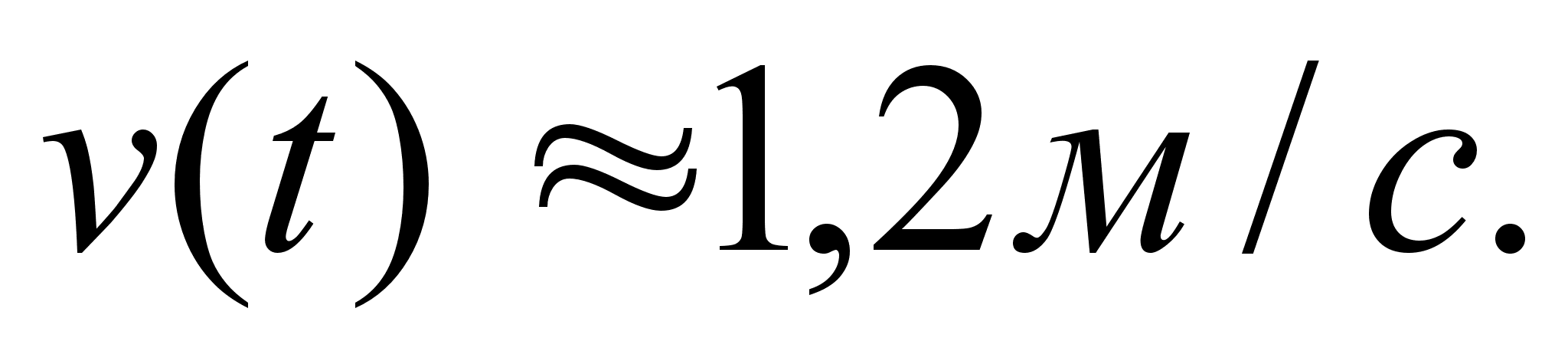
Задача 2
Дождевая капля падает под действием силы тяжести; равномерно испаряясь так, что ее масса m изменяется по закону m(t) = 1 - 2/3t. (m изменяется в граммах, t - в секундах). Через сколько времени после начала падения кинематическая энергия капли будет наибольшей?
Скорость
капли
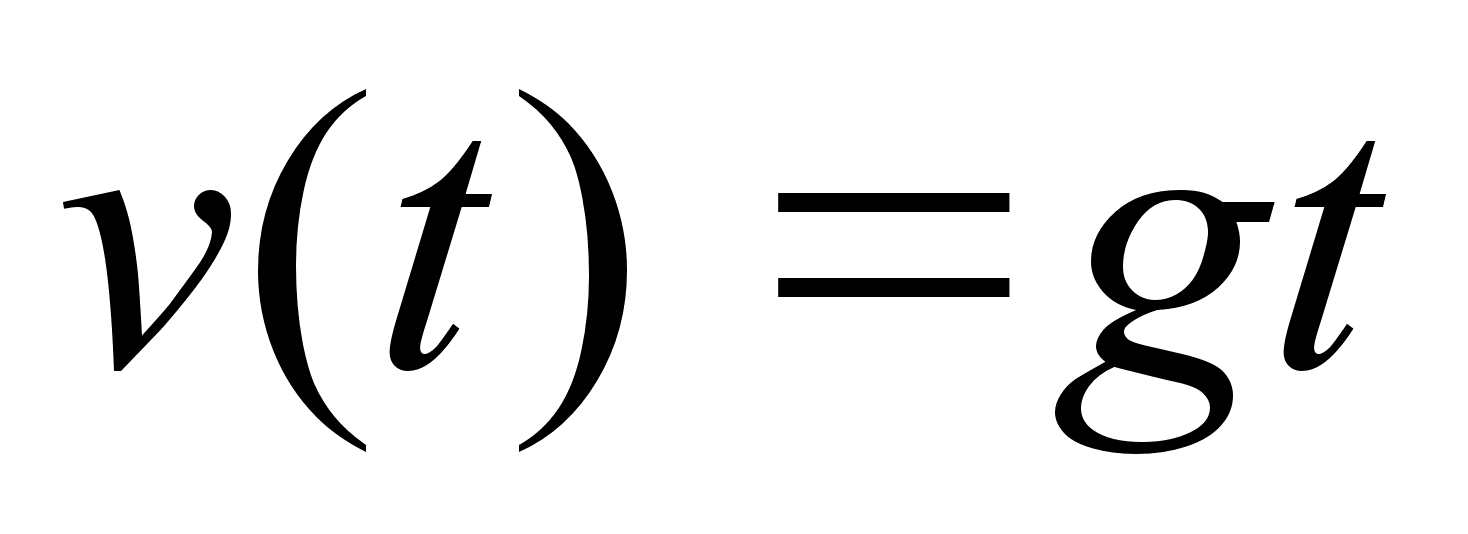 , её кинетическая
энергия
в момент t
равна
, её кинетическая
энергия
в момент t
равна
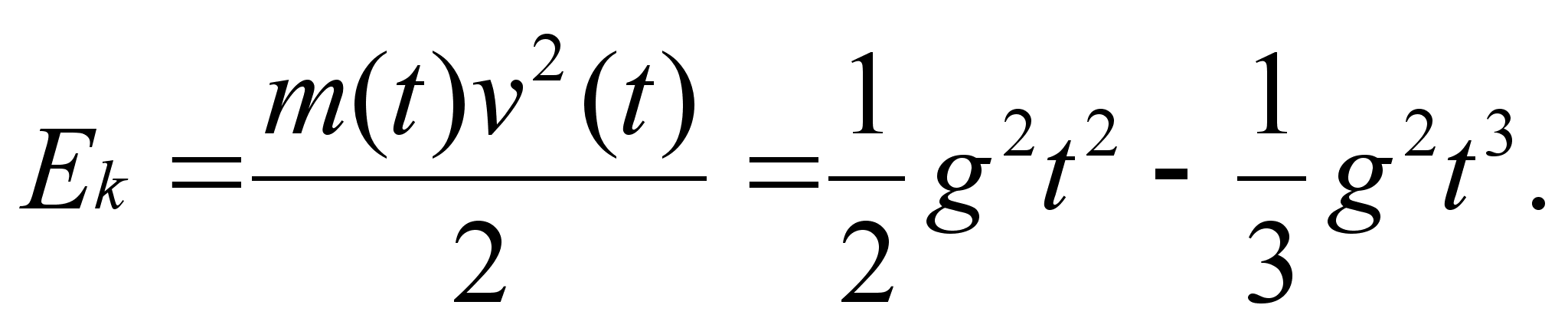
Исследуем
функцию
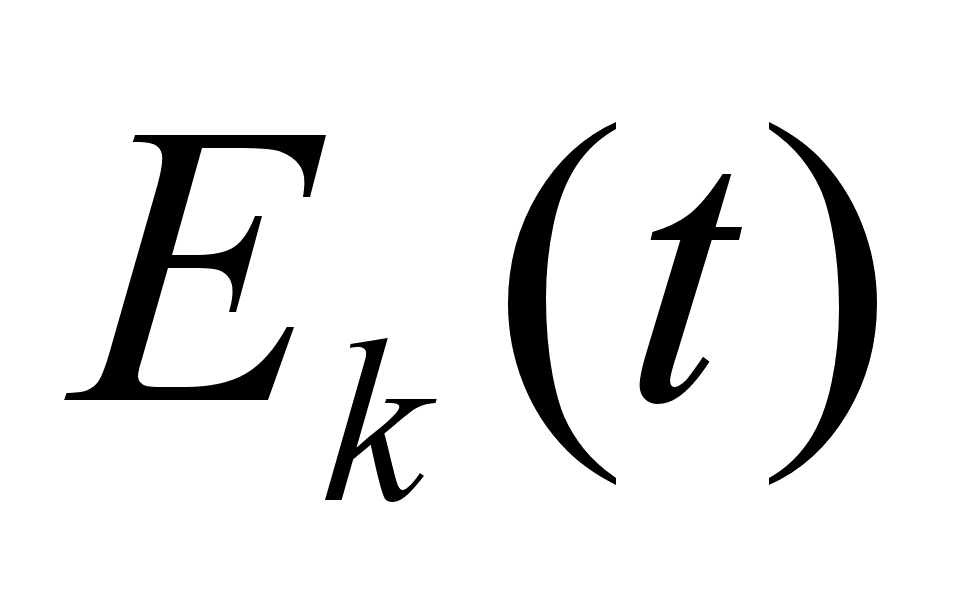 на наибольшее
с помощью
поизводной:
на наибольшее
с помощью
поизводной:
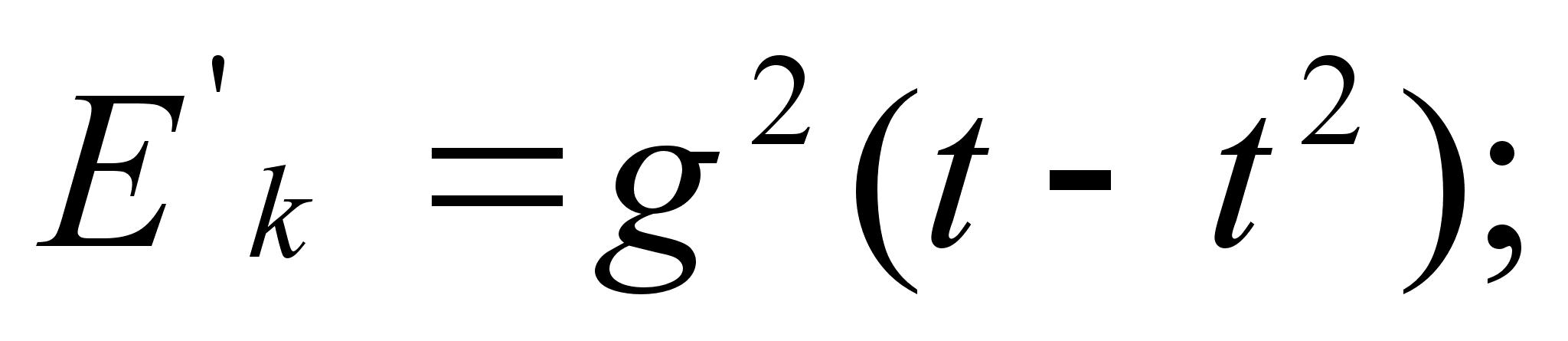
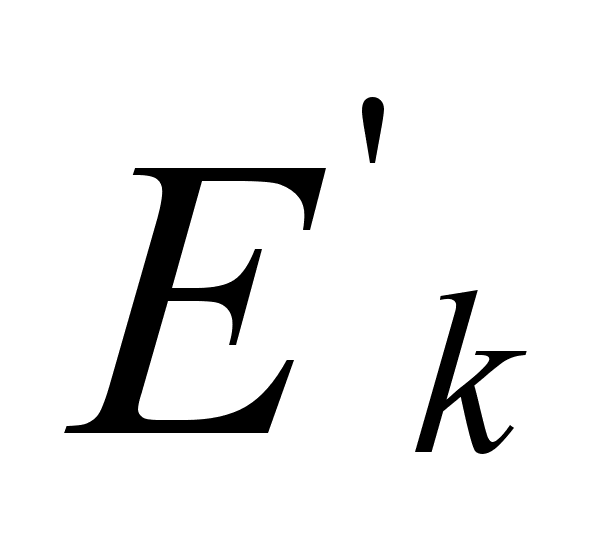 =0
t1=0
t2=1
(t>0)
=0
t1=0
t2=1
(t>0)
При t =1 функция Ek(t) принимает наибольшее значение, следовательно кинетическая энергия падающей капли будет наибольшей через 1сек.
Задача 3
Источник тока с электродвижущей силой Е=220 В и внутренним сопротивлением r = 50 Ом подключен к прибору с сопротивлением R.Чему должно быть равно сопротивление R потребителя, чтобы потребляемая им мощность была наибольшей?
По
закону Ома
сила тока в
цепи есть
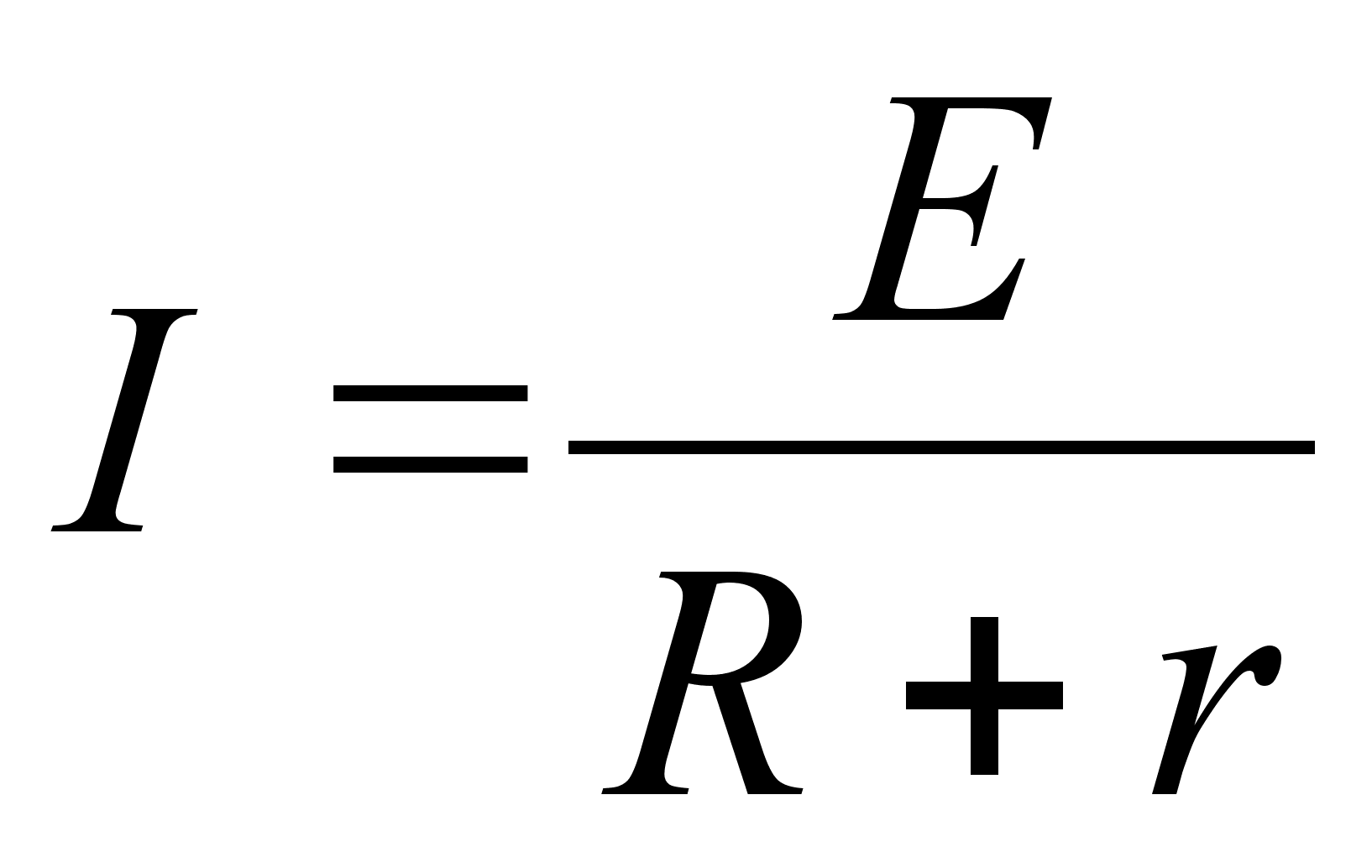

выделяемая
в потребителе
мощность P=I2R,
то
есть
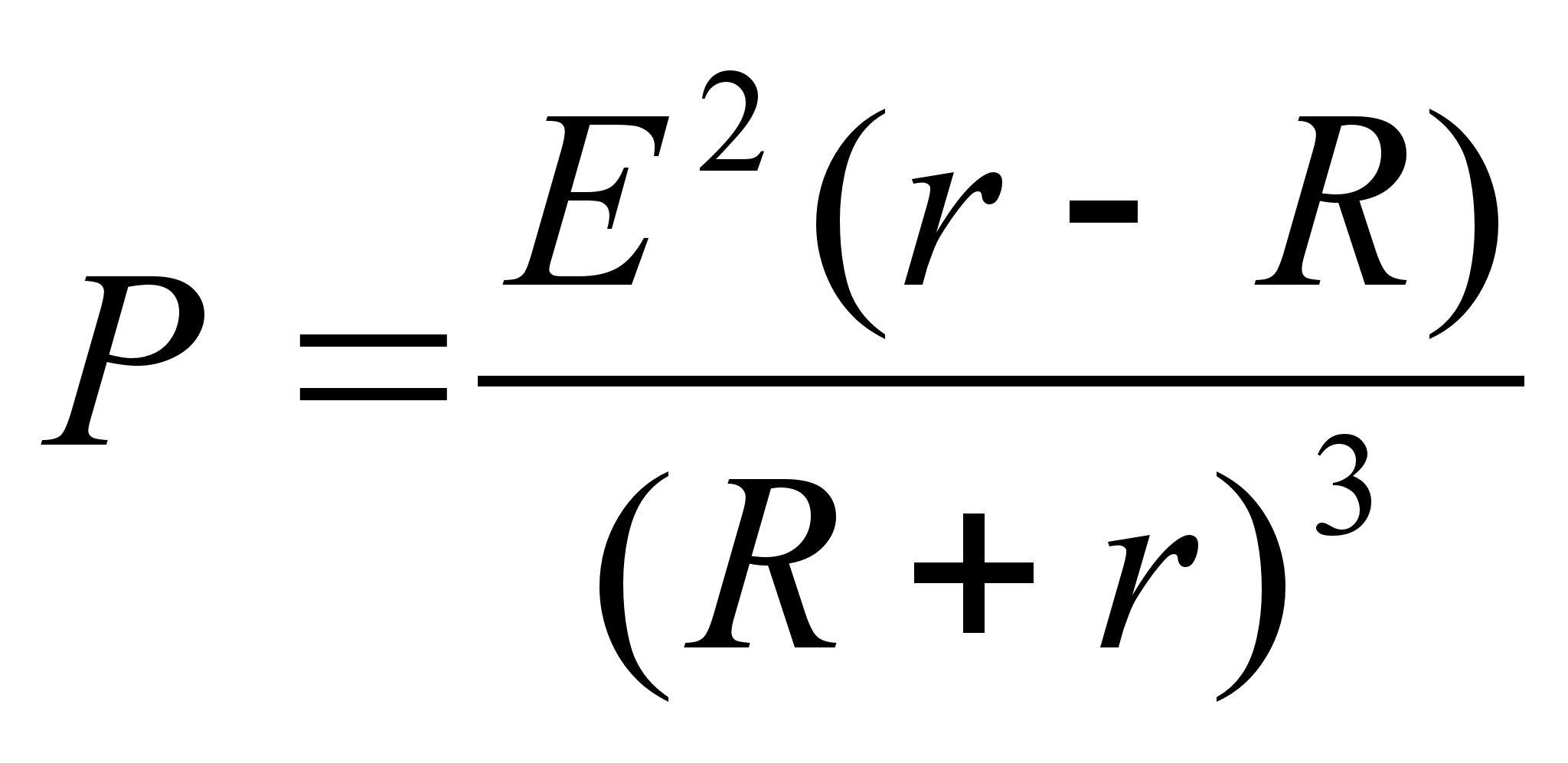
И сследуем
функцию P(R)
на наибольшее
с помощью
производной:
сследуем
функцию P(R)
на наибольшее
с помощью
производной:
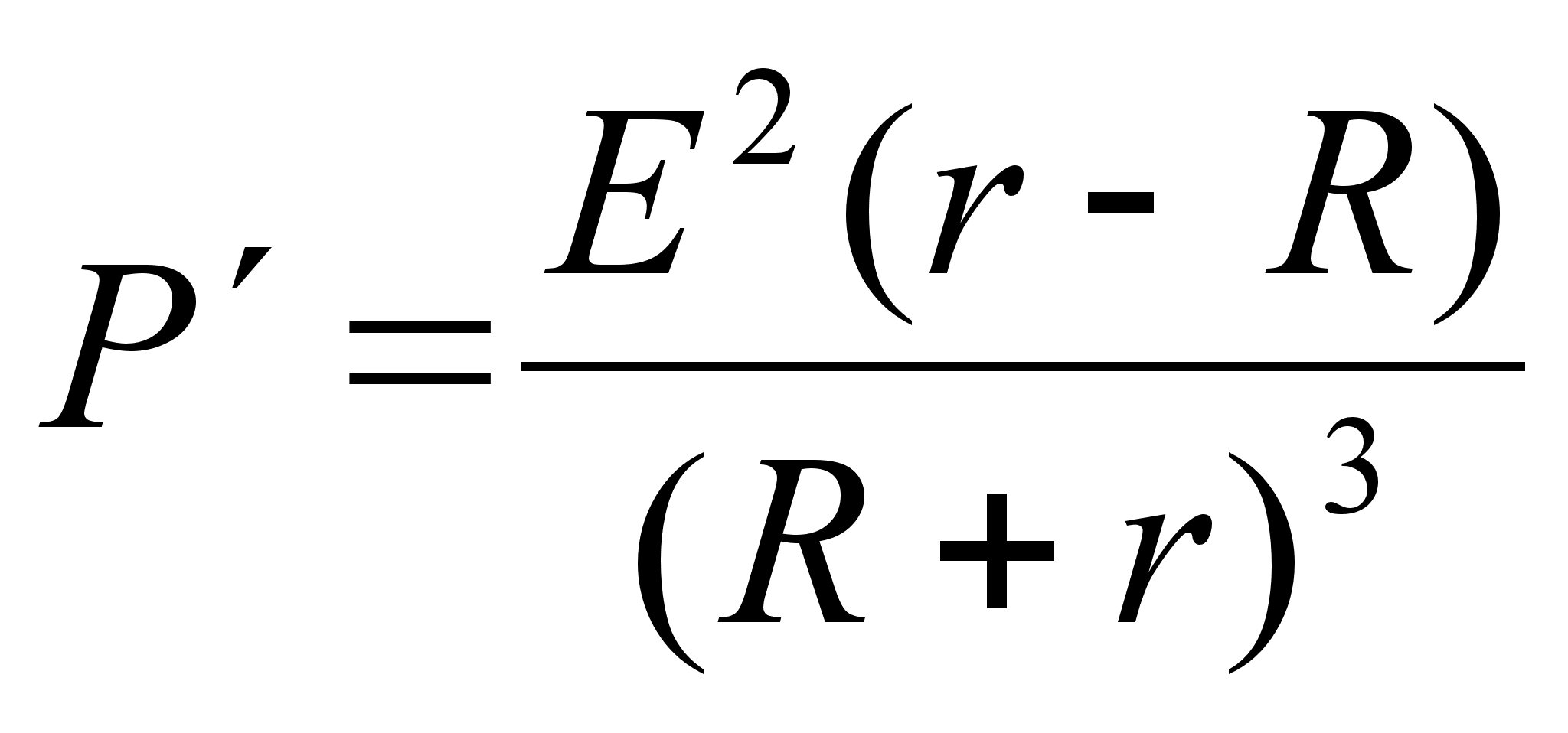 P’(R)
=
0 : r - R = 0, R = r = 50; При
R
= 50 функция P(R)
принимает
наибольшее
значение.
Следовательно,
потребляемая
мощность будет
наибольшей
при сопротивлении
R
=50 Ом.
P’(R)
=
0 : r - R = 0, R = r = 50; При
R
= 50 функция P(R)
принимает
наибольшее
значение.
Следовательно,
потребляемая
мощность будет
наибольшей
при сопротивлении
R
=50 Ом.
О
–
твет: 50 Ом9. Применение производной в алгебре
9.1. Применение производной к доказательству неравенств.
Одно из простейших применений производной к доказательству неравенств основано на связи между возрастанием и убыванием функции на промежутке и знаком ее производной. С помощью теоремы Лагранжа доказана теорема:
Теорема 1.
Если функция
![]() на
некотором
интервале
на
некотором
интервале
![]() имеет
производную
имеет
производную
![]() всюду
на
всюду
на
![]() ,
то
,
то
![]() на
на
![]() монотонно
возрастает;
если же
монотонно
возрастает;
если же
![]() всюду на
всюду на
![]() ,
то
,
то
![]() на
на
![]() монотонно
убывает.
монотонно
убывает.
Очевидным следствием (и обобщением) этой теоремы является следующая:
Теорема
2. Если на
промежутке
![]() выполняется
неравенство
выполняется
неравенство
![]() ,
функция
,
функция
![]() и
и
![]() непрерывны
в точке
непрерывны
в точке
![]() и
и
![]() ,
то на
,
то на
![]() выполняется
неравенство
выполняется
неравенство
![]() .
.
Предлагаю несколько задач на доказательство неравенств с использованием этих теорем.
Задача 1.
Пусть
![]() .Докажите
истинность
неравенства
.Докажите
истинность
неравенства
![]() .
(1)
.
(1)![]()
Решение:
Рассмотрим
на
![]() функцию
функцию
![]() .
Найдем ее
производную:
.
Найдем ее
производную:
![]() .
Видим, что
.
Видим, что
![]() при
при
![]() .
Следовательно,
.
Следовательно,
![]() на
на
![]() убывает так,
что при
убывает так,
что при
![]()
![]() .
Но
.
Но
![]()
![]() Следовательно
неравенство
(1)
Следовательно
неравенство
(1)
![]() верно.
верно.
Задача 2.
Пусть
![]() и
и
![]() положительные
числа,
положительные
числа,
![]() Тогда очевидно,
что
Тогда очевидно,
что
![]() ,
,
![]() .
Можно ли гарантировать,
что неравенство
.
Можно ли гарантировать,
что неравенство
![]() (2)
(2)
верно а) при
![]() ;
б) при
;
б) при
![]() ?
?
Решение:
а) Рассмотрим
функцию
![]() .
Имеем:
.
Имеем:
![]()
Отсюда видно,
что при
![]() функция
функция
![]() возрастает.
В частности,
она возрастает
на интервале
возрастает.
В частности,
она возрастает
на интервале
![]() Поэтому при
Поэтому при
![]() неравенство
(2) справедливо.
неравенство
(2) справедливо.
б) на интервале
![]()
![]() ,
т.е.
,
т.е.
![]() убывает. Поэтому
при любых
убывает. Поэтому
при любых
![]() и
и
![]() ,
для которых
,
для которых
![]() ,
неравенство
(2) неверно, а верно
неравенство
противоположного
смысла:
,
неравенство
(2) неверно, а верно
неравенство
противоположного
смысла:
![]()
Задача 3.
Доказать
неравенство:
![]() при
при
![]() (3).
(3).
Воспользуемся
теоремой 2.
![]() и
и
![]() ,
верно неравенство
,
верно неравенство
![]() :
:
![]() на промежутке
на промежутке
![]() и
выполнимо
условие
и
выполнимо
условие
![]() где
где
![]() ,
в данном случае
равно 0. Следовательно
неравенство
(3) верно.
,
в данном случае
равно 0. Следовательно
неравенство
(3) верно.
Задача4. Доказать
неравенство:
![]()
![]() (4).
(4).
Решение:
![]() ,
,
![]() ;
;
![]()
Неравенство
![]() при любых
при любых
![]() верно. Значит
неравенство
(4) верно.
верно. Значит
неравенство
(4) верно.
Задача5. Доказать,
что если
![]() ,
то
,
то
![]() (5).
(5).
Решение:
Пусть
![]() Тогда
Тогда
![]()
Чтобы найти,
при каких значениях
![]() функция
функция
![]() положительная,
исследуем ее
производную
положительная,
исследуем ее
производную
![]() .
Так как при
.
Так как при
![]()
![]() то
то
![]()
Следовательно,
функция
![]() возрастает
при
возрастает
при
![]() .
Учитывая, что
.
Учитывая, что
![]() и
и
![]() непрерывна,
получаем
непрерывна,
получаем
![]() ,
при
,
при
![]() .
.
Поэтому
![]() возрастает
на рассматриваемом
интервале.
Поскольку
возрастает
на рассматриваемом
интервале.
Поскольку
![]() непрерывна
и
непрерывна
и
![]() то
то
![]() при
при
![]() .
Неравенство
(5) верно.
.
Неравенство
(5) верно.
Задача
6. Выясним, что
больше при
![]() :
:
![]() или
или
![]() .
.
Решение:
Предстоит
сравнить с
числом 1 дробь
![]() .
.
Рассмотрим
на
![]() вспомогательную
функцию
вспомогательную
функцию
![]() .
.
Выясним,
будет ли она
монотонна на
отрезке
![]() .
Для этого найдем
ее производную
(по правилу
дифференцирования
дроби):
.
Для этого найдем
ее производную
(по правилу
дифференцирования
дроби):
![]()
![]() при
при
![]() .
.
В силу теоремы
1 функция
![]() вырастает на
отрезке
вырастает на
отрезке
![]() .
Поэтому, при
.
Поэтому, при
![]()
![]() т.е.
т.е.
![]()
![]() при
при
![]() .
.
При решении
задачи (6)
встретился
полезный
методический
прием, если
нежно доказать
неравенство,
в котором участвует
несколько
букв, то часто
целесообразно
одну из букв
(в данном примере
это была буква
![]() )
считать применимой
(чтобы подчеркнуть
это обстоятельство,
мы ее заменяли
буквой
)
считать применимой
(чтобы подчеркнуть
это обстоятельство,
мы ее заменяли
буквой
![]() ,
а значение
остальных букв
(в данном случае
значение буквы
,
а значение
остальных букв
(в данном случае
значение буквы
![]() )
считать фиксированными.
Иногда приходится
при решении
одной задачи
применить
указанный
прием несколько
раз.
)
считать фиксированными.
Иногда приходится
при решении
одной задачи
применить
указанный
прием несколько
раз.
Задача 7.
Проверить,
справедливо
ли при любых
положительных
![]() неравенство:
неравенство:
![]() (6).
(6).
Решение:
Пусть
![]() Рассмотрим
функцию
Рассмотрим
функцию
![]() .
.
При
![]() имеем
имеем
![]() .
.
Отсюда видно
(теорема 1), что
![]() убывает на
убывает на
![]() Поэтому при
Поэтому при
![]() имеем
имеем
![]() т.е. мы получили
неравенство:
т.е. мы получили
неравенство:
![]() (7).
(7).
Теперь рассмотрим
другую вспомогательную
функцию
![]() .
При
.
При
![]() имеем:
имеем:
![]()
Следовательно,
![]() убывает
на
убывает
на
![]() ,
т.е.
,
т.е.
![]() при
при
![]() значит,
значит,
![]() (8),
(8),
Из неравенств (7) и (8) следует неравенство (6). Для выяснения истинности неравенств иногда удобно воспользоваться следующим утверждением, которое непосредственно вытекает из теоремы 1:
Теорема 3:
Пусть функция
![]() непрерывна
на
непрерывна
на
![]() и
пусть имеется
такая точка
с из
и
пусть имеется
такая точка
с из
![]() ,
что
,
что
![]() на
на
![]() и
и
![]() на
на
![]() .
Тогда при любом
х из
.
Тогда при любом
х из
![]() справедливо
неравенство
справедливо
неравенство
![]() причем равенство
имеет место
лишь при
причем равенство
имеет место
лишь при
![]() .
.
Задача
8. Проверьте,
справедливо
ли для всех
действительных
х следующее
неравенство:
![]()
![]()
Решение: Выясним, где функция возрастает, а где убывает. Для этого найдем производную:
![]() .
.
Видно, что
![]() на
на
![]() и
и
![]() на
на
![]() .
Следовательно,
в силу теоремы
3 т.е. неравенство
(9) справедливо,
причем равенство
имеет место
лишь при
.
Следовательно,
в силу теоремы
3 т.е. неравенство
(9) справедливо,
причем равенство
имеет место
лишь при
![]() .
.
9.2. Применение производной в доказательстве тождеств.
Доказательства тождества можно достигнуть иногда, если воспользоваться одним очевидным замечанием:
Если на некотором интервале функция тождественно равна постоянной, то ее производная на этом интервале постоянно равна нулю:
![]() на
на
![]() на
на
![]() .
.
Задача 1. Проверить тождество:
![]() (1)
(1)
Доказательство: Рассмотрим функцию
![]()
Вычислим ее производную (по х):
![]()
Поэтому
(замечание)
![]() .
Следовательно,
.
Следовательно,
![]() что равносильно
тождеству (1).
что равносильно
тождеству (1).
Задача 2. Проверить тождество:
![]() (2)
(2)
Доказательство: Рассмотрим функцию
![]()
Докажем, что
![]()
Найдем ее производную:
![]()
![]()
![]()
![]()
Значит![]() .
.![]()
При х=0
![]() ,следовательно,тождество
(2) верно.
,следовательно,тождество
(2) верно.
В связи с рассмотренными примерами можно отметить, что при нахождении постоянной, интегрирования С полезно фиксировать значения переменной, по которой производится дифференцирование, таким образом, чтобы получить возможно более простые выкладки.
9.3. Применение производной для упрощения алгебраических и тригонометрических выражений.
Прием использования производной для преобразования алгебраических и тригонометрических выражений основан на том, производная иногда имеет значительно более простой вид, чем исходная функция, благодаря чему, она легко интегрируется, что и позволяет найти искомое преобразование исходного выражения:
Задача
1 Упростить
выражение:
![]()
Решение:
Обозначив
данное выражение
![]() будем иметь:
будем иметь:
![]()
![]()
![]()
![]()
Таким образом,
заданное выражение
(1) равно
![]() .
.
Задача 2. Упростить выражение:
![]()
Решение:
Обозначив
это выражение
через
![]() ,
будем иметь:
,
будем иметь:
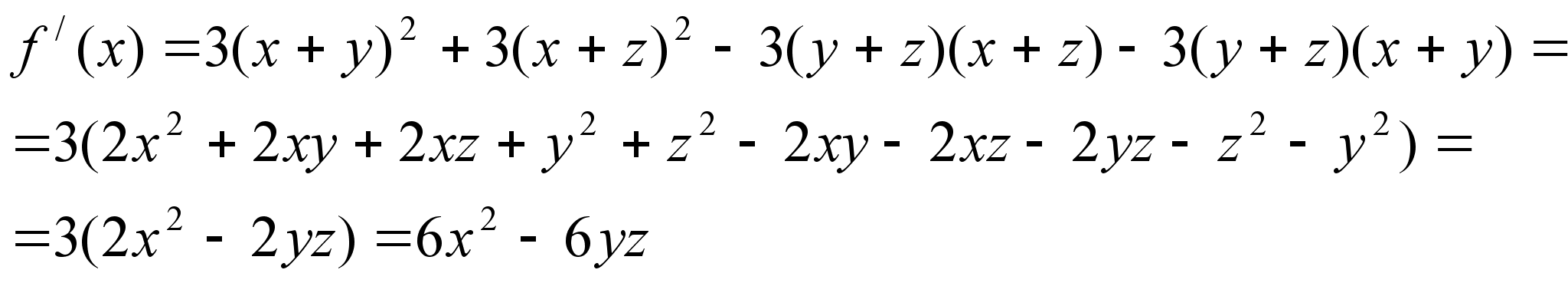
отсюда
![]() .
.
и при
![]() получаем:
получаем:
![]()
Так
что
![]()
Задача 3. Упростить запись функции:
![]() (2)
(2)
Решение: Применение обычного аппарата тригонометрии приведёт к относительно громоздким выкладкам. Здесь удобнее воспользоваться производной:
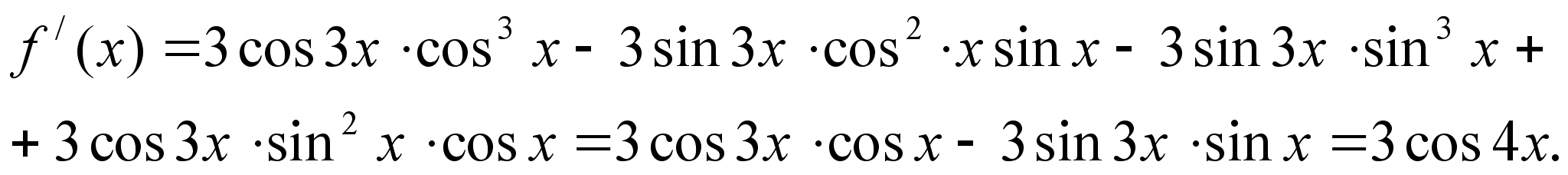
Отсюда
![]()
Найдём
![]() :
:
![]()
Таким
образом функция
(2) равна
![]()
Задача 4. Упростить запись многочлена:
![]() (3)
(3)
Решение:
Обозначим
многочлен (3)
через
![]() и найдём последовательно
первую и вторую
производные
этой функции:
и найдём последовательно
первую и вторую
производные
этой функции:
![]()
![]()
Ясно,
что
![]() Поэтому
Поэтому
![]() ,
где
,
где
![]() ,
найдём
,
найдём
![]() :
при
:
при
![]()
![]() ,
,
![]() .
.
9.4.Разложение выражения на множители с помощью производной.
Задача 1. Разложить на множители выражение:
![]() (1)
(1)
Решение:
Считая
![]() переменной,
а
переменной,
а
![]() и
и
![]() постоянными
фиксированными
(параметрами)
и обозначая
заданное выражение
через
постоянными
фиксированными
(параметрами)
и обозначая
заданное выражение
через
![]() ,
будем иметь:
,
будем иметь:
![]()
Поэтому
![]() (2)
(2)
где
![]() -
постоянная,
т.е. в данном
случае - выражение,
зависящее от
параметров
-
постоянная,
т.е. в данном
случае - выражение,
зависящее от
параметров
![]() и
и
![]() .
Для нахождения
.
Для нахождения
![]() в равенстве
в равенстве
![]() положим
положим
![]() тогда
тогда
![]() .
.
Получим
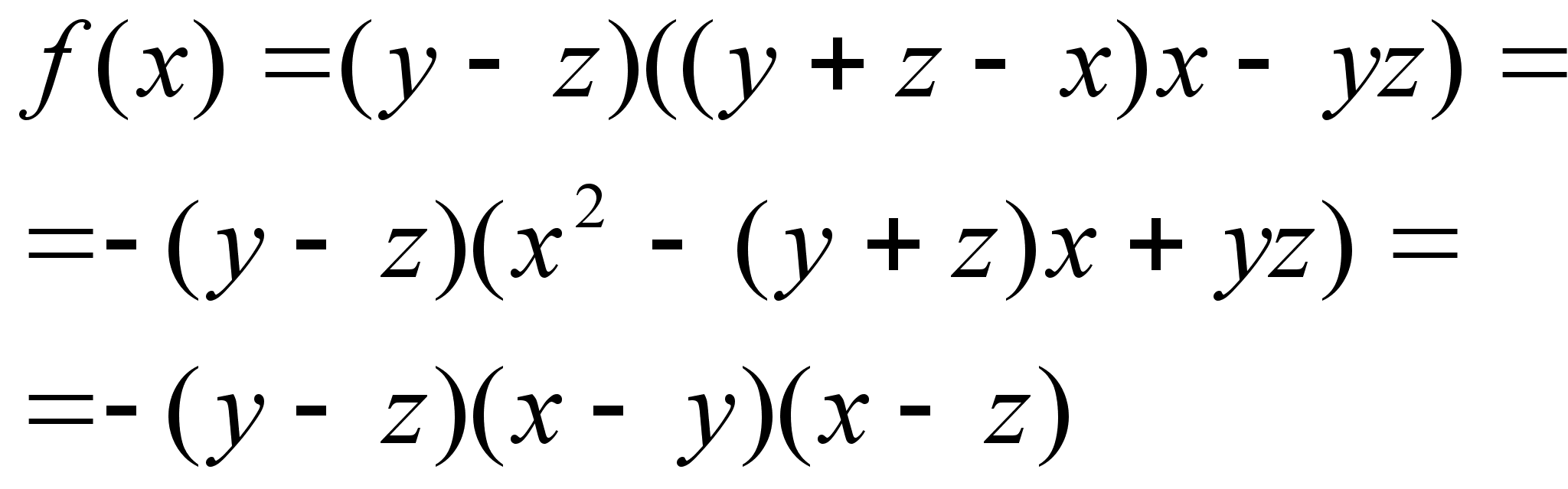
Задача 2. Разложить на множители выражение:
![]() (3)
(3)
Решение:
Поскольку
переменная
![]() входит в данное
выражение в
наименьшей
степени, рассмотрим
его, как функцию
входит в данное
выражение в
наименьшей
степени, рассмотрим
его, как функцию
![]() и будем иметь:
и будем иметь:
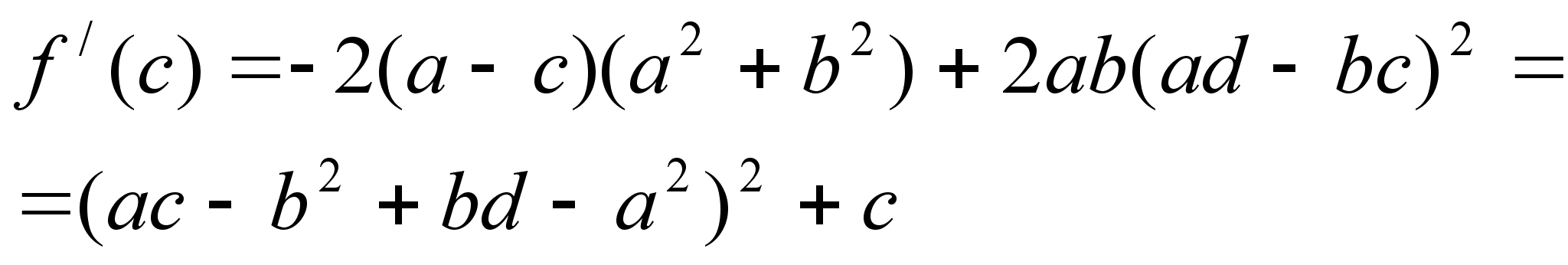
![]() получим:
получим:
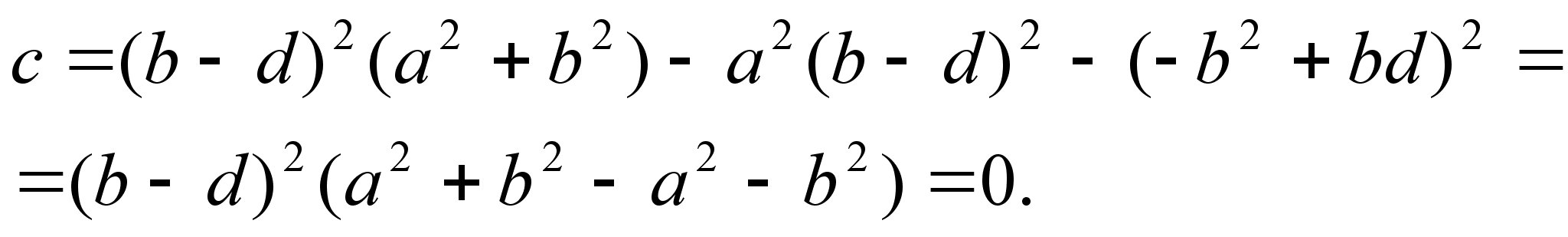
Таким
образом, исходное
выражение (3)
равно
![]()
Задача 3. Разложить на множители выражение:
![]()
Решение:
Обозначив
данное выражение
через
![]() и считая
и считая
![]() и
и
![]() постоянными,
получим:
постоянными,
получим:
![]() откуда
откуда
![]() ,
где
,
где
![]() зависит только
от
зависит только
от
![]() и
и
![]() .
Положив в этом
тождестве
.
Положив в этом
тождестве
![]() ,
получим
,
получим
![]() и
и
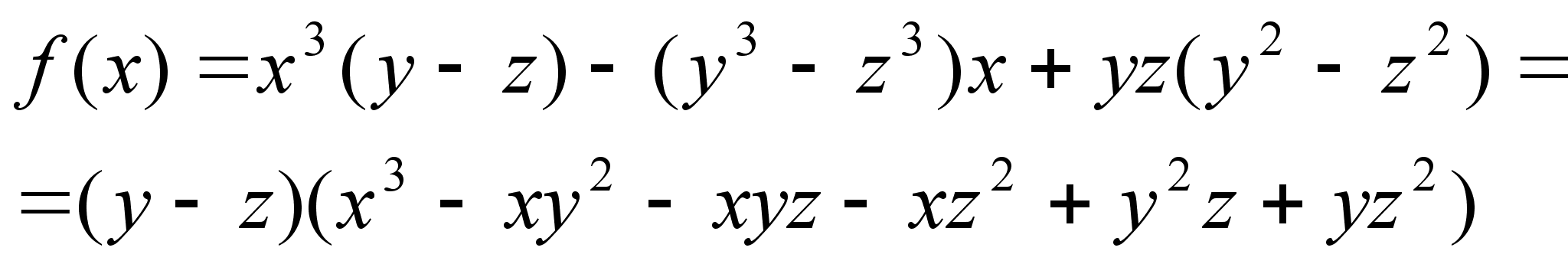
Для
разложения
на множители
второго множителя
используем
тот же приём,
но в качестве
переменной
рассмотрим
![]() ,
поскольку эта
переменная
входит в меньшей
степени, чем
,
поскольку эта
переменная
входит в меньшей
степени, чем
![]() .
Обозначая его
через
.
Обозначая его
через
![]() и считая
и считая
![]() и
и
![]() постоянными,
будем иметь:
постоянными,
будем иметь:
![]()
отсюда:
![]()
![]()
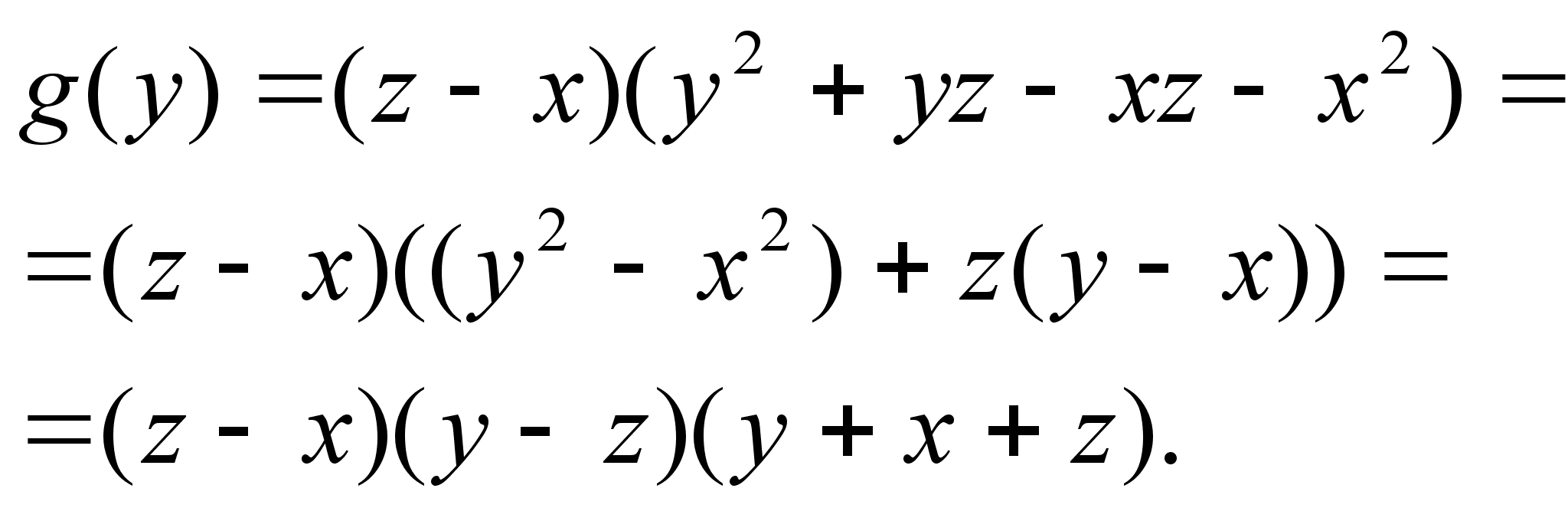
Таким образом исходное выражение (4) равно
![]()
9.5. Применение производной в вопросах существования корней уравнений.
С помощью производной можно определить сколько решений имеет уравнение. Основную роль здесь играют исследование функций на монотонность, нахождение её экстремальных значений. Кроме того, используется свойство монотонных функций:
Задача
1. Если функция
![]() возрастает
или убывает
на некотором
промежутке,
то на этом
промежутке
уравнение
возрастает
или убывает
на некотором
промежутке,
то на этом
промежутке
уравнение
![]() имеет не более
одного корня.
имеет не более
одного корня.
![]() (1)
(1)
Решение:
Область определения
данного уравнения
- промежуток
![]() определение
на этом промежутке
функцию
определение
на этом промежутке
функцию
![]() ,
положив
,
положив
![]()
Тогда,
на
![]()
![]()
![]()
![]()
![]()
![]() ,
,
и
таким образом
функция
![]() -
возрастающая,
так что данное
уравнение (1)
не может иметь
более одного
решения.
-
возрастающая,
так что данное
уравнение (1)
не может иметь
более одного
решения.
Задача
2. При каких
значениях
![]() имеет решения
уравнение
имеет решения
уравнение
![]() (2)
(2)
Решение:
область определения
уравнения -
отрезок
![]() ,
рассмотрим
функцию
,
рассмотрим
функцию
![]() ,
положив
,
положив
![]()
Тогда
на открытом
промежутке
![]()
![]()
![]() ,
так что
,
так что
![]() -
единственная
критическая
точка функции
-
единственная
критическая
точка функции
![]() ,
являющаяся,
очевидно, точкой
максимума.
Поскольку
,
являющаяся,
очевидно, точкой
максимума.
Поскольку
![]()
![]() то
то
![]() примет наибольшее
значение при
примет наибольшее
значение при
![]() ,
а наименьшее
значение - при
,
а наименьшее
значение - при
![]() .
.
Так
как функция
![]() непрерывна,
то её область
значений
представляет
собой отрезок
непрерывна,
то её область
значений
представляет
собой отрезок
![]() ,
между её наименьшим
и наибольшим
значением.
Другими словами,
исходное уравнение
(2) имеет решения
при
,
между её наименьшим
и наибольшим
значением.
Другими словами,
исходное уравнение
(2) имеет решения
при
![]() .
.
Заключение
Настоящая работа даёт учащимся новый подход к многим преобразованиям в математике, которые стандартным путём трудно разрешимы или разрешимы, но громоздкими способами. Рассмотренные подходы нестандартного характера для учащихся покажутся новыми и необыкновенными, что расширит их кругозор и повысит интерес к производной.
Итак, геометрический смысл производной: производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.
Физический смысл производной: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0
Экономический смысл производной: производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.
Производная находит широкое приложение в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени; для нахождения наибольших и наименьших величин.
Производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул.
Наиболее актуально использование производной в предельном анализе, то есть при исследовании предельных величин (предельные издержки, предельная выручка, предельная производительность труда или других факторов производства и т. д.).
Производная применяется в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем
Знание производной позволяет решать многочисленные задачи по экономической теории, физике, алгебре и геометрии.