Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Пирамида
Реферат: Пирамида
Экзаменационный реферат по
Геометрии
На тему: «Пирамида – неопознанный многогранник»
Ученика школы №975
11 класса «Б»
Полтавского Станислава
Москва 2003
Содержание.
1. Содержание …………………………………………….…2
2. Введение ………………………………………………..….3
3. Пирамида - чудо света ……………………..………....4
4. Феномен пирамидных конструкций ………….......7
5. Пирамида в геометрии …………............................9
6. Теоремы …………………………………………….….....12
7. Задачи …………………………………....................….13
8. Используемые источники ……....................………19
Введение.
Представьте себе, что в некоторой плоскости (будем считать ее горизонтальной) расположен некоторый многоугольник, обозначаемый буквой М, а над этой плоскостью взята некоторая точка А. Рассмотрим отрезок, одним концом которого является некоторая точка фигуры М, а вторым — точка А. Всевозможные такие отрезки, вместе взятые, образуют многогранник, называемый пирамидой с основанием М и вершиной А.
Поверхность пирамиды кроме основания содержит еще ряд боковых граней. Каждая из них представляет собой треугольник, основанием которого является одна из сторон многоугольника М, а вершиной — точка А.
Таким образом, пирамида содержит одну грань — основание, которое может быть многоугольником с любым числом сторон, а все остальные грани (называемые боковыми)
представляют собой треугольники, имеющие основанием одну общую сторону, причем все боковые грани имеют одну общую вершину. Это описание пирамиды можно принять за ее определение. Например, пакеты молока часто делают в форме треугольной пирамиды, т. е. пирамиды с треугольным основанием
Если основанием пирамиды является правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, перпендикулярен плоскости основания, то пирамида называется правильной Четырехскатная крыша дома имеет форму четырехугольной правильной пирамиды.


Пирамида - чудо света.
Прежде чем приступить к описанию грандиозного и знаменитого заупокойного ансамбля в Гизе, приведем рассказ Геродота, этого греческого "журналиста", который черпал сведения у иностранцев, живших в Египте. Он завещал нам удивительные, бесценные документы.
"Хеопс, — пишет он, — оставил после себя грандиозное произведение: свою пирамиду. Говорят, что Египет до эпохи правления Рампсинитов был процветающей, хорошо управляемой страной. Хеопс, наследовавший Рампсинитам, приказал всем египтянам работать на него. Одним было приказано перетаскивать к Нилу камни, выломанные в карьерах Арабских гор; другие должны были нагружать их на суда для перевозки через реку и тащить их к Ливийским горам. На стройке постоянно находились сто тысяч рабочих, которые сменялись каждые три месяца.
Они уже потратили 10 лет на прокладку дороги, по которой перетаскивали камни, но это еще было ничто по сравнению со строительством самой Пирамиды. Дорога была длиной в 5 стадий (923,5 м), 10 оргий в ширину (18,47 м) и в самом высоком месте имела подъем в 8 оргий (14,78 м). Она была выложена полированными камнями с изображениями животных. Понадобилось 10 лет, чтобы завершить дорогу и построить подземные камеры, которые должны были служить могилами. Гробницы были сооружены на плато: там возвышаются Пирамиды на острове, образованном отводным каналом. Сама пирамида потребовала 20 лет работы. Она квадратная. Каждая ее сторона равна 8 метрам (246,26 м) и такого же размера ее высота. Камни отполированы и тщательно пригнаны; каждый из них не меньше 30 ступней (9,24 м)".
После этого вступления Геродот рассказывает историю сооружения Большой Пирамиды, сообщая очень подробные детали, начиная от характеристики типового египетского стиля и кончая расходами на строительство этого уникального монумента.
"Эта пирамида, — продолжает он, — сначала была построена в виде большой лестницы, составленной из того, что одни называют зубцами, а другие ступенями. Такая форма позволяла поднимать остальные камни с помощью машины, состоящей из коротких балок. Когда камень был водружен на первую ступень, его перекладывали на другую машину, стоявшую там, откуда камень поднимался на следующую ступень, где его помещали на третью машину, так как машин было столько же, сколько и ступеней. Или это была переносная машина, которую перемещали с этажа на этаж, освободив от камня. Я описываю здесь два приема, как мне об этом рассказывали.
Таким образом сначала заканчивали вершину, потом переходили по этажам вниз и завершали основание пирамиды. На этой пирамиде есть надписи, в которых указано, сколько средств было израсходовано на приобретение хрена, лука и головок чеснока, чтобы прокормить рабочих, и если я правильно запомнил слова переводчика, читавшего мне эту надпись, сумма расходов доходила до 6 000 талантов серебра, что составляет 41 884 кг. Если это действительно так, то сколько же талантов серебра могли они израсходовать на железные инструменты, с помощью которых работали, на пищу и одежду для рабочих? Потому что, кроме работ по сооружению храма, они потратили еще немало времени, как я думаю, на обработку и транспортировку камней и строительство подземных камер".
Четыре века спустя после Геродота историк Диодор из Сицилии (I в. до н.э.) посетил Египет и, увидев пирамиды, причислил их к одному из семи чудес света. Как и его предшественник, Диодор изумлен этим монументом. "Нужно признать, — утверждает он, — что эти монументы намного превосходят все", что можно увидеть в Египте, не только огромностью своих размеров и средств, потраченных на них, но также и красотой".
Диодор Сицилийский сообщает нам свою версию о строительстве пирамид. Он также говорит о трех пирамидах как о заупокойном ансамбле IV династии, из которых Большая Пирамида, — конечно же, самое значительное и чудесное сооружение, но которое не может рассматриваться отдельно от других.
Как и Геродот, Диодор Сицилийский оценивает в 6 000 талантов сумму расходов на хрен, лук и чеснок для строителей Большой Пирамиды; но в противоположность Геродоту, он не считает, что эти монументы служили гробницами фараонов, которых, по его мнению, хоронили тайно в засекреченных местах. Мы не будем цитировать дальше текст Диодора, который более или менее совпадает с текстом Геродота. Мы хотели лишь показать, что все великие писатели античности были одинаково поражены самобытностью и красотой египетских погребальных монументов.
Прибывшему в Гизу туристу открывается одна из прекраснейших картин, какую когда-либо создавала рука человека. Египетская поговорка "Всё боится времени, но время боится Пирамид" как нельзя лучше применима к этому месту.
Гиза — это современное название большого каирского некрополя, занимающего примерно 2000 кв.м. Сюда входят Сфинкс и три Большие Пирамиды: Хеопса, Хефрена и Микерина. Последняя имеет еще три малых пирамиды-спутницы. Три монумента расположены по диагонали, но таким образом, что ни один не заслоняет солнце другим. Каждая пирамида включает, в соответствии с типовым планом, заупокойный храм вверх по течению Нила и заупокойный храм вниз по течению, а также соединяющий их коридор. Ансамбль Пирамиды Хеопса почти полностью разрушен; ансамбль Пирамиды Хефрена, напротив, в большей части сохранился.
Пирамида Хеопса — самая большая из трех. Имевшая вначале 146 м высоты, сегодня она достигает лишь 137 м, а на месте вершины образовалась площадка шириной 10 м. Пирамида полностью лишилась наружной
|
|
облицовки, так что гигантские каменные блоки обнажились и позволяют подняться по ним до самой вершины. Нужно сказать, что открывающаяся сверху панорама вполне вознаграждает потраченные на подъем силы.
Пирамида Хефрена
Пирамида Хефрена — единственная сохранившая на вершине полированную облицовку. Хотя ее высота меньше, чем у предыдущей, ее вершина находится на одинаковом с ней уровне, так как она стоит на более высоком месте. Первоначально ее основание было облицовано розовым гранитом. И наконец, меньшая из трех, но более пропорциональная Пирамида Микерина едва достигает 66 м в высоту. В 1500 году она еще имела гранитную облицовку, которая в наши дни полностью исчезла. Погребальная камера заключала величественный базальтовый саркофаг, украшенный под "фасад храма", что было довольно распространенным приемом декорирования в эпоху Древнего царства. К сожалению, саркофаг затонул у побережья Португалии при кораблекрушении во время перевозки его в Англию.
Перед Пирамидой Микерина возвышаются три Пирамиды-спутницы, которые еще меньше, чем спутницы Пирамиды Хеопса. Пирамида-спутница с восточной стороны, изначально облицованная розовым гранитом, была, без сомнения, предназначена для супруги фараона Хармер-Нехти II.
Феномен пирамидных конструкций.
Первым
из наших современников, кто установил ряд необычных явлений, связанных с
пирамидой, был французский ученый Антони Бови.
Исследуя пирамиду Хеопса в течение тридцатых годов, он обнаружил, что тела
мелких животных, случайно попавших в царскую комнату, мумифицировались.
Вернувшись во Францию, он построил деревянную модель пирамиды с длиной стороны
основания около одного метра. Сориентировав ее по сторонам света и поместив в
место расположения царской комнаты, т.е. приблизительно на 1/3 расстояния от
основания до вершины тело мертвой кошки, он через несколько дней обнаружил ее
мумифицировавшейся. Того же эффекта он достигал и с другими органическими
веществами, которые, мумифицируясь, не портились и не гнили. Исследования А.
Бови не вызывали никакого интереса до пятидесятых годов, пока ими не
заинтересовался чешский инженер Карел Дрбан, который не только воспроизвел
результаты опытов А.Бови, но и обнаружил связь между формой пространства
пирамиды и биологическими и физико-химическими процессами, происходящими в этом
пространстве. Оказалось, что изменяя размеры пирамиды можно воздействовать на
происходящие процессы, ускоряя или замедляя их. Весьма знаменитым открытие
К.Дрбана оказалось то, что энергия пирамиды, сориентированной сторонами к
геомагнитным полюсам, затачивает помещенное в нее бритвенное лезвие, при
условии его расположения на уровне ![]() высоты
от основания пирамиды под прямым углом к геомагнитному меридиану.
высоты
от основания пирамиды под прямым углом к геомагнитному меридиану.
Изобретение было запатентовано и выпускался пластмассовый прибор
"Бритвенный затачиватель "Пирамида Хеопса"", позволявший
многократно использовать одно и то же бритвенное лезвие. Hачиная с пятидесятых
годов, патентов становится все больше и больше. Оказалось, что энергия формы
пирамиды "умеет делать" очень многое: растворимый кофе, постояв над
пирамидой, приобретает вкус натурального; дешевые вина значительно улучшают
свои вкусовые качества; вода приобретает свойства способствовать заживлению,
тонизирует организм, уменьшает воспалительную реакцию после укусов, ожогов и
действует, как естественное вспомогательное средство для улучшения пищеварения;
мясо, рыба, яйца, овощи, фрукты мумифицируются, но не портятся; молоко долго не
киснет; сыр не плесневеет. Если сидеть под пирамидой, то улучшается процесс
медитации, уменьшается интенсивность головной и зубной боли, ускоряется
заживление ран и язв. Пирамиды устраняют вокруг себя геопатогенное воздействие
и гармонизируют внутреннее пространство помещений. Исследованиями, проведенными
в шестидесятые годы известным каббалистом и египтологом Энелем (его настоящее
имя Михаил Владимирович Сарятин, 1883 - 1963 гг.), было показано, что излучение
пирамиды имеет сложную структуру и особые свойства. Им было выделено несколько
лучей: луч, названный Пи, под влиянием которого происходит разрущение
опухолевых клеток; луч, вызывающий мумификацию (высушивание) и уничтожение
микроорганизмов и таинственный луч Омега, под влиянием которого продукты
длительное время не портятся и который оказывает благотворное влияние на
организм человека. Энелем впервые было высказано предположение о том, что
воздействию именно этого концентрированного луча подвергались посвящаемые во
время инициации в саркофаге царской комнаты.
Последующими исследованиями было показано, что благодаря широкому спектру
частот, часть которых идентична частотам колебаний здоровых клеточных структур
биологических объектов, излучением пирамиды оказывается гармонизирующее,
натраивающее на оптимальное функционирование воздействие. Французскими
радиэстезистами Л.Шомери и А. де Белизалом(1976) впервые было высказано
предположение о роли Великой Пирамиды как передающей станции. Они показали, что
благодаря огромной массе, излучение формы пирамиды, достигало такой силы, что с
очень большого расстояния с помощью модели пирамиды можно было определить это
излучение, и без компаса точно сориентировать.по ней маршрут корабля в море или
каравана в пустыне. Особенно интриговала ученых существующая в конструкции
Великой пирамиды особенность - она не была закончена до вершины. В
действительности ее вершина образована не четырьмя гранями, а платформой с
размерами 6х6 метров. Проведенные Д.Шомери и А. де Белизалом радиэстезические
исследования позволили установить, что такой конструкцией формировалась ложная
вибрационная призма, которая создавала излучение, вертикально опускающиеся к
основанию пирамиды. Комната фараона, находяшаяся вне области распространения
этого пучка, избегала этого влияния, но оно должно было захватывать до сих пор
не найденную подземную комнату, размещенную значительно ниже уровня земли.
Полученные французскими исследователями данные, а также установленное Энелем (1958)
предназначение загадочного сооружения из четырех элементов, создающего
излучение, направленное на саркофаг царской комнаты, позволяет утверждать, что
Великая Пирамида использовалась как приемо-передающее многофункциональное
устройство с огромным диапазоном действия, внутри которого проявлялись иные
законы, чем в окружающем ее мире.
Проведенные в 1969 г. компьютерные исследования Л.Альвареса, установившего в
пирамиде Хефрена счетчики космического излучения, вызвали в научном мире
огромный резонанс геометрия пирамиды непонятным образом нарушала работу
приборов, вынудив ученых прекратить их проведение. Эта попытка, как и многие
другие, выявила еще одну особенность изучения пирамид - с каждым новым
исследованием возникает больше новых вопросов, чем ответов.
Пирамида в геометрии.
Пирамида - (от греч. pyramis, род. п. pyramidos), многогранник, основание которого многоугольник, а остальные грани треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырехугольные и т. д.
Общая вершина боковых граней называется вершиной пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
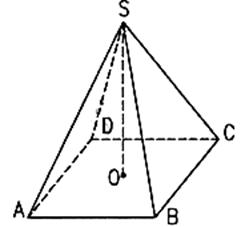
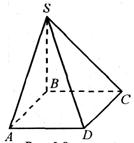
SABCD – четырёхугольная пирамида;
ABCD – основание пирамиды;
rSAB; rSBC; rSDC; rSDA – боковые грани пирамиды;
S – вершина пирамиды;
SA; SB; SC; SD – боковые рёбра пирамиды
SO – Высота пирамиды
Пирамида правильная – пирамида, у которой в основании лежит правильный многоугольник, а высота, опущенная из вершины пирамиды на плоскость основания, является отрезком, соединяющим вершину пирамиды с центром основания.
Свойства правильной пирамиды:
1. Всё боковые рёбра правильной пирамиды равны между собой.
2. Все боковые грани являются равными между собой равнобедренными треугольниками.
3. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на высоту боковой грани, которая называется апофемой.
![]()
![]() – периметр основания,
– периметр основания,
![]() - апофема.
- апофема.
Объем любой пирамиды равен одной трети произведения площади основания на высоту:
![]()
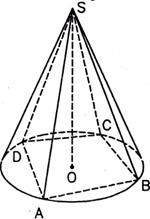
Пирамидой, вписанной в конус, является такая пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра такой пирамиды являются образующими конуса.
|
|
SABCD – пирамида, вписанная в конус.
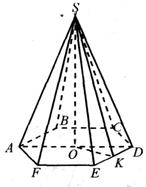
Пирамидой, описанной около конуса, является такая пирамида, основание которой есть многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней такой пирамиды являются касательными плоскостями конуса.
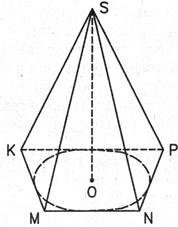
SKMNP – пирамида, описанная около конуса.
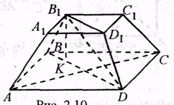
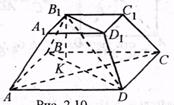
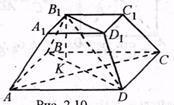
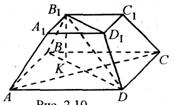
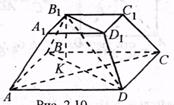
Пирамида усечённая - пирамида, которая получается следующим способом: берется произвольная пирамида, и через точку бокового ребра проводится плоскость, параллельная основанию пирамиды. Данная плоскость разделила пирамиду на две фигуры: подобную исходной пирамиду и многогранник, который называется усеченной пирамидой. Основаниями усеченной пирамиды служат подобные многоугольники.
Если усеченная пирамида получается из правильной пирамиды, то она называется правильной усеченной пирамидой. Боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями. Высота боковой грани называется апофемой правильной усеченной пирамиды. Перпендикуляр, опущенный из точки верхнего основания на нижнее, называется высотой усеченной пирамиды.
Площадь полной поверхности усеченной пирамиды равна сумме площадей оснований и боковых граней.
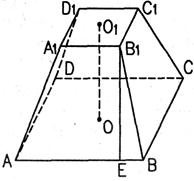
ABCDA1B1C1D1 – усечённая правильная пирамида,
O1O – высота,
B1E – апофема усечённой пирамиды.
Объём усечённой пирамиды вычисляется по формуле:
![]()
![]() – высота усеченной пирамиды,
– высота усеченной пирамиды,
![]() и
и![]() -
площади оснований усеченной пирамиды.
-
площади оснований усеченной пирамиды.
Площадь боковой поверхности правильной усеченной пирамиды вычисляется по формуле:
![]()
![]() и
и![]() -
периметры оснований усечённой правильной пирамиды,
-
периметры оснований усечённой правильной пирамиды,
![]() - апофема.
- апофема.
Теоремы.
- Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Доказательство:
Боковые
грани правильной пирамиды – равные равнобедренные треугольники, основания
которых – стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой
поверхности пирамиды равна сумме произведений сторон основания на половину
апофемы d. Вынося множитель ![]() за скобки, получим в
скобках сумму сторон основания пирамиды, т.е. его периметр.
за скобки, получим в
скобках сумму сторон основания пирамиды, т.е. его периметр.
- Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Задачи.
Задача №1
Построим линию пересечения плоскости грани МАВ пирамиды МАВCD с плоскостью грани MCD.
Решение: Плоскости МАВ и MCD имеют по условию общую точку М. Значит, по аксиоме (если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку) они пересекаются по прямой, проходящей через точку М. Найдем еще одну общую точку этих плоскостей. В соответствии с условием прямые АВ и CD лежат в одной плоскости. Построим точку их пересечения:
![]()
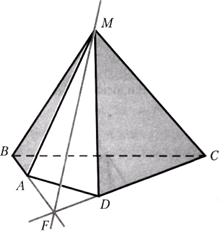
Точка F принадлежит прямой АВ, две точки которой лежат в плоскости МАВ. Тогда по аксиоме (Если две точки прямой принадлежат плоскости, то все точки прямой, определяемой ими, лежат в этой плоскости) и точка F лежат в плоскости МАВ.
Аналогично заключаем, что точка F лежит и в плоскости MCD. Таким образом, точка F — это вторая общая точка плоскостей МАВ и MCD. Итак, прямая MF — это искомая линия пересечения плоскостей МАВ и MCD.
Задача №2
На ребре МА пирамиды MABCD
взята точка Р, а в ее гранях MCD и МВС — соответственно точки Q и R. Построим
основной след секущей плоскости ![]() , проходящей через точки Р, Q и R.
, проходящей через точки Р, Q и R.
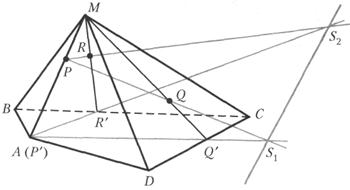
Решение: 1) Построим точки
Р', Q' и R' — проекции соответственно точек Р, Q и R на плоскость ABC из
центра М. Ясно, что точка Р' совпадает с точкой ![]() ,
,![]() .
.
Так как прямые МР и MQ пересекаются, то по
теореме (Через две пересекающиеся прямые проходит плоскость, и притом одна)
через них
проходит плоскость. По теореме этой плоскости принадлежат прямые PQ и P'Q'.
Построим точку ![]() .
.
Так как точка ![]() лежит на прямой PQ, две точки
которой принадлежат плоскости
лежит на прямой PQ, две точки
которой принадлежат плоскости![]() , то по аксиоме (Если две точки
прямой принадлежат плоскости, то все точки прямой, определяемой ими, лежат в
этой плоскости) точка
, то по аксиоме (Если две точки
прямой принадлежат плоскости, то все точки прямой, определяемой ими, лежат в
этой плоскости) точка ![]() принадлежит плоскости
принадлежит плоскости ![]() . Аналогично
заключаем, что точка
. Аналогично
заключаем, что точка ![]() принадлежит плоскости ABC. Итак,
плоскости
принадлежит плоскости ABC. Итак,
плоскости ![]() и
ABC имеют общую точку
и
ABC имеют общую точку ![]() . Тогда по аксиоме (если две
плоскости имеют общую точку, то они пересекаются по прямой, проходящей через
эту точку) эти плоскости пересекаются по прямой, проходящей через точку
. Тогда по аксиоме (если две
плоскости имеют общую точку, то они пересекаются по прямой, проходящей через
эту точку) эти плоскости пересекаются по прямой, проходящей через точку ![]()
Построим еще одну общую
точку плоскостей а и ABC. Например,
точку ![]() .Проведем
прямую
.Проведем
прямую ![]()
![]() Так как точки
Так как точки ![]()
![]() этой прямой лежат в
плоскости
этой прямой лежат в
плоскости ![]() ,
то по аксиоме (Если две точки прямой принадлежат плоскости, то все точки
прямой, определяемой ими, лежат в этой плоскости) прямая
,
то по аксиоме (Если две точки прямой принадлежат плоскости, то все точки
прямой, определяемой ими, лежат в этой плоскости) прямая ![]()
![]() лежит в плоскости
лежит в плоскости ![]() . Аналогично приходим к
выводу, что прямая
. Аналогично приходим к
выводу, что прямая ![]()
![]() лежит в плоскости ABC. Таким
образом, прямая
лежит в плоскости ABC. Таким
образом, прямая ![]()
![]() — это линия пересечения
плоскости а с плоскостью ABC, т.е. она является основным следом плоскости
— это линия пересечения
плоскости а с плоскостью ABC, т.е. она является основным следом плоскости ![]() .
.
Задача №3
Центр верхнего основания куба с
ребром, равным ![]() , соединен с
серединами сторон нижнего основания, которые также соединены в последовательном
порядке. Вычислить полную поверхность полученной пирамиды.
, соединен с
серединами сторон нижнего основания, которые также соединены в последовательном
порядке. Вычислить полную поверхность полученной пирамиды.
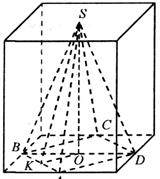
Решение: Так как ребро куба равно а, то сторона основания пирамиды
SABCD
равна ![]() Учитывая,
что ОК =
Учитывая,
что ОК = ![]() , найдём апофему пирамиды:
, найдём апофему пирамиды: ![]()
Значит,
![]() ,
, 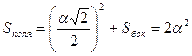
Ответ:
![]()
Задача №4
Апофема правильной
шестиугольной пирамиды равна h, а двугранный угол при основании равен ![]() . Найти полную поверхность
пирамиды.
. Найти полную поверхность
пирамиды.
|
|
Решение: Так
как ![]() , то
, то ![]() .
.
Основание
пирамиды – правильный шестиугольник, поэтому ![]() и
и
![]() . Тогда
. Тогда ![]() ,
т.е.
,
т.е. ![]() ,
,
![]() . Таким образом,
. Таким образом, ![]() ,
, ![]()
Окончательно
находим ![]()
Ответ: ![]()
Задача №5
В основании пирамиды лежит
квадрат. Две боковые грани перпендикулярны плоскости основания, а две другие
наклонены к нему под углом ![]() . Среднее
по величине боковое ребро равно
. Среднее
по величине боковое ребро равно ![]() . Найти
объём и полную поверхность пирамиды.
. Найти
объём и полную поверхность пирамиды.
|
|
Решение: По
условию, ![]() ,
, ![]() ,
, ![]() . Откуда
. Откуда ![]() .
.
Находим ![]() .
.
Полная поверхность
выразится так: ![]() , поскольку
, поскольку
![]() ,
, ![]() .
.
Но 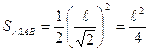 ,
, ![]()
Итак, ![]()
Ответ: ![]() ;
; ![]() .
.
Задача №6
Определить объём правильной четырёхугольной усечённой пирамиды, если её диагональ равна 18 см., а длины сторон оснований 14 и 10 см..
|
|
|
|
|
|
|
|
|
|
Решение:
Искомый объём выражается формулой ![]() , где
, где ![]()
![]() .
Найдём
.
Найдём ![]()
Имеем ![]() . Так как
. Так как ![]() - равнобедренная трапеция,
то
- равнобедренная трапеция,
то
![]() и
и ![]() т.е.
т.е.
![]() Итак,
Итак, ![]()
Ответ: ![]()
|
|
Используемые источники.
1. Весь Египет (Джованна Маджи, Паоло Джамбоне)
2. Математика. Справочник школьника (Г. Якушева)
3. Геометрия 10-11 класс (Л. С. Атасян, В. Ф. Бутузов)
4. Что такое. Кто такой. (А.Г. Алексин, С.П. Алексеев)
5. Геометрия (В.Н. Литвиненко)
6. http://www.devious.by.ru
7. Сборник задач по Математике (М.И. Сканави)