Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Обработка результатов эксперимента
Реферат: Обработка результатов эксперимента
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА МАТЕМАТИКИ
СЕМЕСТРОВАЯ РАБОТА ПО СТАТИСТИКЕ
«Обработка результатов эксперимента»
Вариант №999
ВЫПОНИЛ: студент группы АТ–312
Литвинов Александр Владимирович
ПРОВЕРИЛ: Африкян Арсен Джуванович
ВОЛГОГРАД 2003
Исследования прочности 250 образцов бетона на сжатие образуют совокупность независимых и равноточных измерений случайной величины Х (МПа):
21,8
24,7
25,3
19,8
22,1
22,2
25,9
24,0
24,9
24,1
22,0
22,9
24,7
24,1
21,5
21,6
21,7
21,8
24,5
24,6
24,2
19,3
24,6
24,9
24,1
22,8
25,4
22,0
24,5
23,1
24,6
24,7
19,1
24,8
24,1
24,0
22,7
22,8
22,1
22,2
24,3
24,4
19,2
25,7
22,8
22,1
25,1
25,5
25,6
22,3
25,7
23,1
23,0
23,5
23,3
23,4
23,9
25,7
25,3
25,8
25,0
20,1
24,1
20,0
23,7
23,8
20,9
20,1
18,0
20,7
20,1
20,5
23,7
23,3
24,7
23,8
20,6
22,6
22,7
19,5
22,2
20,7
23,7
24,2
20,3
20,8
20,0
25,2
25,6
19,6
20,3
20,9
20,6
26,8
21,0
21,9
22,7
22,3
21,1
21,7
21,1
26,2
26,6
21,3
21,0
26,7
26,3
21,5
24,7
21,6
23,9
23,1
21,7
24,3
24,7
24,0
21,8
20,8
20,2
21,1
21,2
21,6
26,8
26,1
21,7
21,3
21,4
22,8
22,0
21,9
21,6
27,2
28,0
21,7
21,0
22,6
22,7
21,2
21,6
21,7
22,1
22,5
22,6
22,7
22,8
21,3
21,8
21,6
22,1
22,5
22,6
22,6
22,3
22,0
22,9
22,1
22,7
23,6
22,3
22,4
22,9
24,8
24,0
24,3
24,4
24,9
22,6
22,1
22,7
21,9
21,1
22,4
22,9
19,9
22,6
21,7
21,1
21,1
22,1
22,5
22,3
22,8
19,6
22,0
23,2
23,6
23,7
23,3
23,8
22,3
23,7
23,1
24,7
25,6
25,0
23,1
23,6
23,7
21,0
21,3
21,4
21,9
23,8
23,1
23,0
23,3
23,4
22,4
24,6
22,9
23,3
23,8
23,0
23,3
22,6
23,9
23,1
23,9
23,6
23,1
23,9
23,1
23,7
23,1
23,5
23,6
23,7
23,8
23,1
24,6
24,7
24,3
24,8
23,2
22,6
22,7
23,2
23,6
20,4
23,7
23,4
19,3
23,9
23,6
23,1
23,5
20,7
20,6
23,6
23,6
Требуется:
1. вычислить точечные оценки для математического ожидания, среднеквадратического отклонения, коэффициентов асимметрии и эксцесса;
2. составить интервальный статистический ряд распределения относительных частот и построить гистограмму и полигон относительных частот;
3. найти эмпирическую функцию распределения и построить ее график и график кумуляты;
4. исходя из общих представлений о механизме образования СВ Х, а также по виду гистограммы и полигона относительных частот и вычисленным числовым характеристикам, выдвинуть гипотезу о виде распределения СВ Х; записать плотность распределения вероятностей и функцию распределения для выдвинутого гипотетического закона, заменяя параметры закона вычисленными для них оценками;
5. по критерию согласия χ2 Пирсона проверить соответствие выборочного распределения гипотетическому закону для уровня значимости q = 0,05;
6. вычислить интервальные оценки для математического ожидания и среднеквадратического отклонения, соответствующие доверительным вероятностям γ = 0,95 и γ = 0,99.
Решение:
Изучение непрерывных случайных величин начинается с группировки статистического материала, т. е. разбиения интервала наблюдаемых значений СВ Х на k частичных интервалов равной длины и подсчета частот попадания наблюдаемых значений СВ Х в частичные интервалы. Количество выбираем равным 10 (k = 10).
Разобьем весь диапазон значений на 10 интервалов (разрядов). Длину частичного интервала определим по формуле:
;
Шкала интервалов и
группировка исходных статистических данных сведены в таблицу. В результате
получили статистический ряд распределения частот (
):
| Интервалы наблюдаемых значений СВ Х, МПа | [18;19) | [19;20) | [20;21) | [21;22) | [22;23) | [23;24) | [24;25) | [25;26) | [26;27) | [27;28] |
|
Частота mi |
1 | 9 | 20 | 41 | 56 | 60 | 38 | 16 | 7 | 2 |
Для получения
статистического ряда частостей разделим частоты mi на объем выборки n. В
результате получим интервальный статистический ряд распределений частостей 
:
| Интервалы наблюдаемых значений СВ Х, МПа | [18;19) | [19;20) | [20;21) | [21;22) | [22;23) | [23;24) | [24;25) | [25;26) | [26;27) | [27;28] |
|
Частости mi/n |
0,004 | 0,036 | 0,080 | 0,164 | 0,224 | 0,240 | 0,152 | 0,064 | 0,028 | 0,008 |
|
F* (x) (накопленные частости) |
0,004 | 0,040 | 0,120 | 0,284 | 0,508 | 0,748 | 0,900 | 0,964 | 0,992 | 1,000 |
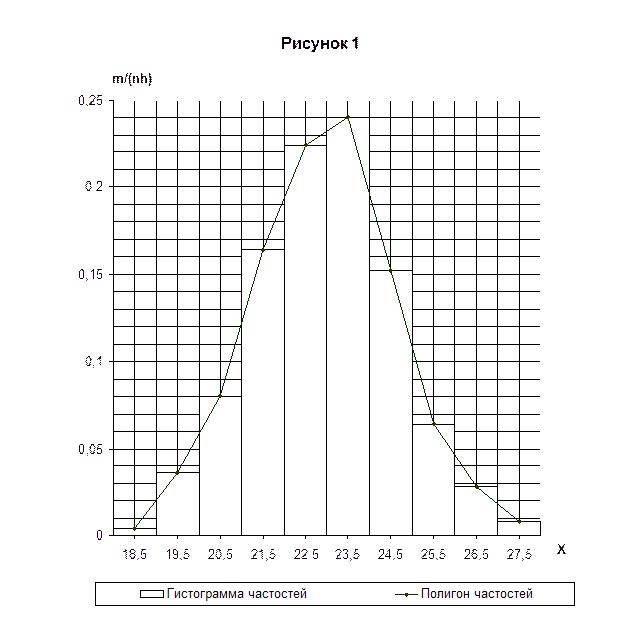
Для построения гистограммы частостей на оси Ox откладываются частичные интервалы, на каждом из них строится прямоугольник, площадь которого равна частости данного частичного интервала. Если частости отнести к серединам частичных интервалов, то полученная замкнутая линия образует полигон частостей. На рисунке 1 изображена гистограмма и полигон частостей.
Значения эмпирической функции распределения выписаны в последней строке статистического ряда распределения частостей. Запишем значения эмпирической функции распределения в аналитическом виде:
0, если x ≤ 18;
0,004, если 18 < x ≤ 19;
0,04, если 19 < x ≤ 20;
0,12, если 20 < x ≤ 21;
0,284, если 21 < x ≤ 22;
F*(x) = 0,508, если 22 < x ≤ 23;
0,748, если 23 < x ≤ 24;
0,9, если 24 < x ≤ 25;
0,964, если 25 < x ≤ 26;
0,992, если 26 < x ≤ 27;
1, если 27 < x ≤ 28;
1, если x ≥ 28;
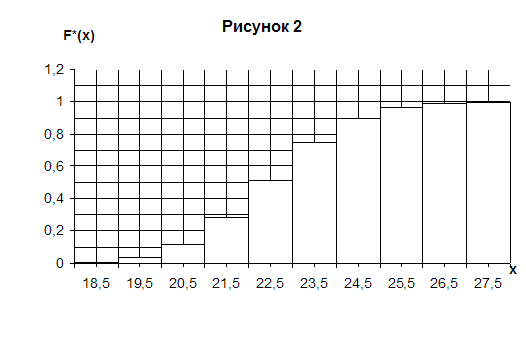
График эмпирической функции изображен на рисунке 2.
В тех
случаях, когда наблюдаемые значения случайной величины задаются многозначными
числами и объем выборки достаточно велик (n > 25), вначале
целесообразно найти среднюю арифметическую по формуле 
а за тем перейти к
вычислению центральных моментов порядка k (k = 2, 3, 4):
|
Интервалы наблюдаемых значений СВ Х, МПа |
Середины интервалов xi |
Частоты mi |
|
|
|
|
| [18;19) | 18,5 | 1 | -4,44 | 19,71 | -87,53 | 388,63 |
| [19;20) | 19,5 | 9 | -30,96 | 106,50 | -366,37 | 1260,31 |
| [20;21) | 20,5 | 20 | -48,80 | 119,07 | -290,54 | 708,91 |
| [21;22) | 21,5 | 41 | -59,04 | 85,02 | -122,43 | 176,29 |
| [22;23) | 22,5 | 56 | -24,64 | 10,84 | -4,77 | 2,10 |
| [23;24) | 23,5 | 60 | 33,60 | 18,82 | 10,54 | 5,90 |
| [24;25) | 24,5 | 38 | 59,28 | 92,48 | 144,26 | 225,05 |
| [25;26) | 25,5 | 16 | 40,96 | 104,86 | 268,44 | 687,19 |
| [26;27) | 26,5 | 7 | 24,92 | 88,72 | 315,83 | 1124,34 |
| [27;28] | 27,5 | 2 | 9,12 | 41,59 | 189,64 | 864,75 |
| Итого | 250 | 0 | 687,61 | 57,07 | 5443,47 | |
Следовательно,
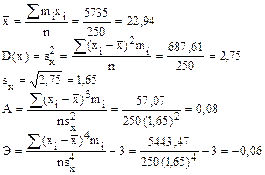
Для предварительного выбора закона распределения вычислим вначале средние квадратические ошибки определения асимметрии
и эксцесса
Критерием
«нормальности» распределения прочности бетона на сжатие является равенство нулю
асимметрии и эксцесса. Из приведенных расчетов видно, что выборочные
коэффициенты асимметрии 
и
эксцесса Э отличаются от нуля не более чем на удвоенные средние квадратические
ошибки их определения, что соответствует нормальному распределению. Вид
полигона и гистограммы частостей также напоминает нормальную кривую (кривую Гаусса).
Можно предположить, прочность бетона на сжатие (СВ Х) изменяется под влиянием большого числа факторов, примерно равнозначных по силе. Поэтому, исходя из «технологии» образования СВ Х, т. е. механизма образования отклонений прочности от некоторого номинального значения, можно предположить, что распределение прочности бетона на сжатие является нормальным.
Плотность вероятности нормального распределения имеет вид
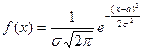
Найдём точечные оценки параметров a и σ нормального распределения методом моментов:
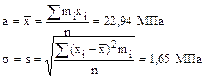
Следовательно, плотность вероятности предполагаемого нормального распределения имеет вид
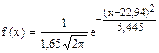
Функция распределения предполагаемого нормального распределения имеет вид
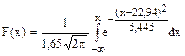
Используя
нормированную функцию Лапласа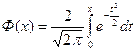 
,
функцию нормального распределения можно записать в виде
Проведем
проверку гипотезы о нормальном распределении СВ Х (прочности бетона на сжатие)
с помощью критерия согласия 
для этого
интервалы наблюдаемых значений нормируют, т.е. выражают их в единицах среднего
квадратического отклонения s: 
, причем
наименьшее значение 
полагают равным 
, наибольшее 
. Далее вычисляют
вероятности попадания СВ Х, имеющей нормальное распределение, с параметрами а =
22,94, σ = 1,65 в частичные интервалы (хi-1; хi) по формуле
,
где
.
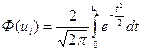Например,
вероятность того, что СВ Х (прочность бетона на сжатие) попадает в первый частичный
интервал (
;19) , равна
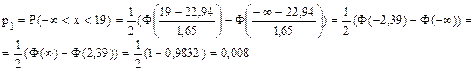
Аналогично
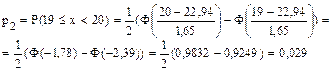
и т. д.
После этого вычисляют теоретические (модельные) частоты нормального
распределения 
и наблюдаемое
значение критерия 
Затем по
таблицам квантилей распределения 
по
уровню значимости q = 0,05 и числу степеней свободы ‚ 
(k — число интервалов; r — число параметров предполагаемого
распределения СВ Х) находят критическое значение 
.
Если 
, то считают, что нет
оснований для отклонения гипотезы о нормальном распределении прочности бетона
на сжатие.
В
противном случае, т. е. если 
,
считается, что гипотеза нормального распределения прочности бетона на сжатие не
согласуется с экспериментальными данными.
Вычисления,
необходимые для определения наблюдаемого значения выборочной статистики 
приведем в таблице:
| Интервалы наблюдаемых значений СВ Х, МПа |
Частоты mi |
Нормированные интервалы [ui, ui-1] |
pi |
npi |
|
|
| [18;19) | 1 | (-∞;-2,39) | 0,008 | 2,00 | 1 | 0,05 |
| [19;20) | 9 | [-2,39;-1,78) | 0,029 | 7,25 | 3,06 | 0,42 |
| [20;21) | 20 | [-1,78;-1,18) | 0,081 | 20,25 | 0,06 | 0,00 |
| [21;22) | 41 | [-1,18;-0,57) | 0,168 | 42,00 | 1 | 0,02 |
| [22;23) | 56 | [-0,57;0,04) | 0,231 | 57,75 | 3,06 | 0,05 |
| [23;24) | 60 | [0,04;0,64) | 0,223 | 55,75 | 18,06 | 0,32 |
| [24;25) | 38 | [0,64;1,25) | 0,154 | 38,50 | 0,25 | 0,01 |
| [25;26) | 16 | [1,25;1,85) | 0,074 | 18,50 | 6,25 | 0,34 |
| [26;27) | 7 | [1,85;2,46) | 0,025 | 6,25 | 0,56 | 0,09 |
| [27;28] | 2 | [2,46;+∞) | 0,007 | 1,75 | 0,06 | 0,03 |
|
|
250 | 1.000 | 250,0 |
|
||
Замечание. Наименьшее значение
стандартизованной переменной 
заменено 
, наибольшее значение 
заменено 
. Эта замена произведена для того, чтобы
сумма теоретических (модельных) частот npi была равна объему выборки.
В
результате вычислений получили 
. Найдем
по таблице квантилей 
распределения по
уровню значимости α = 0,05 и числу степеней 
критическое
значение 
. Так как 
, то нет оснований для отклонения
гипотезы о нормальном распределении прочности бетона на сжатие.
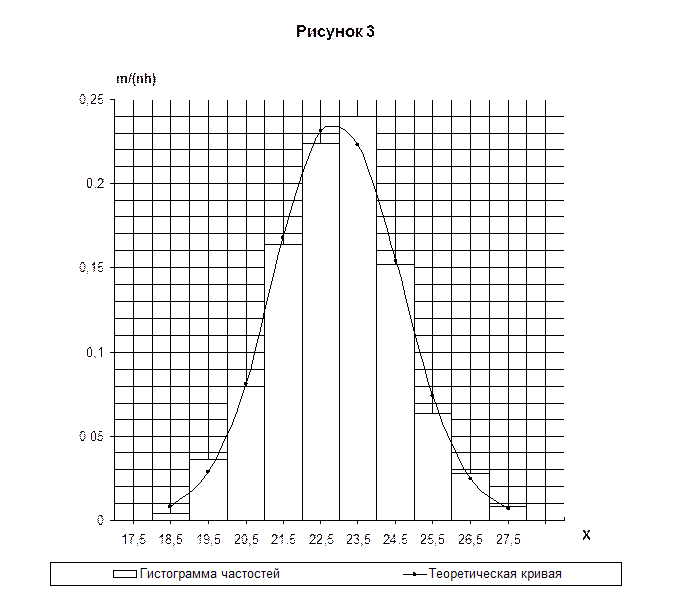
Построим нормальную кривую. Для этого из середин частичных интервалов восстании перпендикуляры высотой pi/h (pi — вероятность попадания СВ Х в частичный интервал; h — длина интервала). На рисунке 3 концы этих перпендикуляров отмечены кружками. Полученные точки соединены плавной кривой. Сравнение гистограммы и нормальной кривой наглядно показывает, что нормальная кривая хорошо сглаживает гистограмму относительных частот.
Найдем
интервальные оценки параметров нормального распределения. Для вычисления
доверительного интервала накрывающего математическое ожидание прочности бетона
на сжатие (СВ Х), найдем по таблицам квантилей распределения Стьюдента по заданной
доверительной вероятности 
и числу
степеней свободы‚ 
квантиль
.
Вычислим предельную погрешность интервального оценивания
Искомый доверительный интервал для математического ожидания
Смысл полученного результата: если будет произведено достаточно большое число выборок по 250 исследований прочности образцов бетона на сжатие, то в 95% из них доверительный интервал накроет математическое ожидание прочности бетона и только в 5% случаев математическое ожидание может выйти за границы доверительного интервала.
Для
нахождения доверительного интервала, накрывающего неизвестное среднее
квадратическое отклонение σ с заданной вероятностью 
, найдем по доверительной
вероятности 
и числу степеней свободы 
‚ два числа; 
. Искомый доверительный
интервал
Полученный результат означает, что если будет произведено достаточно большое число выборок по 250 исследований прочности образцов бетона на сжатие, то в 95% из них доверительный интервал накроет среднее квадратическое отклонение σ и только в 5% среднее квадратическое отклонение σ можёт выйти за границы доверительного интервала.
