Реферат: Нахождение неопределенных интегралов

Контрольная работа (вариант 8)

Найти неопределенные интегралы:

2. Интегрирование по частям

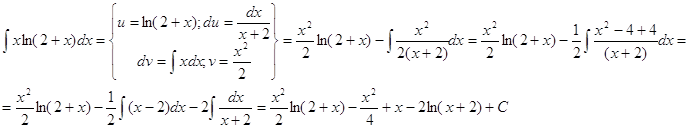
Вычислить определенные интегралы:

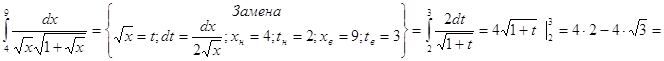
=8-6,92=1,08

Интегрирование по частям

5. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями

. Построить чертеж.

Решение.

В декартовой системе координат построим линии и найдем точки их пересечения.

Объем тела вращения по формуле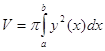

Точки пересечения линий

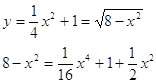
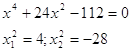
(второй вариант не подходит, т.к. отрицателен)

Отсюда

Границы фигуры:

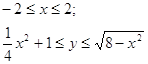
Фигура симметрична относительно оси ОУ, поэтому

Объем тела

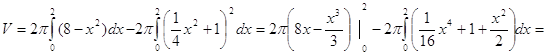
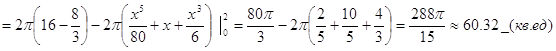
6. Методом наименьших квадратов найти эмпирическую формулу вида y=ax+b для функции, заданной следующей таблицей:

X	3.3	3.5	3.7	3.9	4.1
Y	13	13.5	11.4	11.2	9.7

Изобразить графически таблично заданную и соответствующую линейную функции. По эмпирической формуле вычислить значение переменной при х=4,0

Решение

Заполним таблицу

			2
1	3,3	13	10,89	42,9
2	3,5	13,5	12,25	47,25
3	3,7	11,4	13,69	42,18
4	3,9	11,2	15,21	43,68
5	4,1	9,7	16,81	39,77
S	18,5	58,8	68,85	215,78

Составим для определения коэффициентов систему уравнений вида:

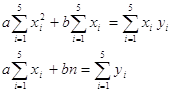
Получим

Решая систему методом исключения определяем:

Искомая эмпирическая формула y=28.23-4.45x

Значение переменной при x=4.0

y=28.23-4.45*4=10.43

7. Исследовать сходимость ряда.

Исследуем ряд сначала на абсолютную сходимость. Общий член ряда

В свою очередь ряд расходится как гармонический. Значит абсолютной сходимости у исходного ряда нет. Исследуем на условную сходимость по признаку Лейбница.

при

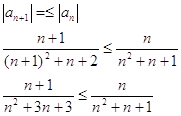
действительно для

По признаку Лейбница, исходный ряд сходится условно.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.monax.ru/