
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Численные методы
Реферат: Численные методы
МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ.
Розглянемо чисельні методи розв’язання систем лінійних алгебраїчних рівнянь
Ax=f T (1)
де A - матриця m*m, x = ( x1, x2 , ... ,xm ) - шуканий вектор,
Т
f =(f1, f2, ... , fm) -заданий вектор.
Припускаємо,
що
![]() та
визначник
матриці
А
відмінний від
нуля, так що
існує єдиний
розв’язок х.
З курсу алгебри
відомо,
що
систему
(1)
можна розв’язати
за формулами
Крамера*. Для
великих m
цей
спосіб практично
нереалізований
тому,
що потребує
порядку m!
aрифметичних
дій. Тому широко
використовуються
інші методи
розв’язання,
наприклад,
метод
Гаусса**,
який потребує
та
визначник
матриці
А
відмінний від
нуля, так що
існує єдиний
розв’язок х.
З курсу алгебри
відомо,
що
систему
(1)
можна розв’язати
за формулами
Крамера*. Для
великих m
цей
спосіб практично
нереалізований
тому,
що потребує
порядку m!
aрифметичних
дій. Тому широко
використовуються
інші методи
розв’язання,
наприклад,
метод
Гаусса**,
який потребує
![]() дій.
дій.
Методи чисельного розв’язання системи (1) поділяються на дві групи:
-прямі методи;
-ітераційні методи.
У прямих (або точних) методах розв’язок x системи (1) відшукується за скінченну кількість арифметичних дій. Внаслідок похибок заокруглення прямі методи насправді не приводять до точного розв’язку системи (1) і назвати їх точними можливо лише залишаючи осторонь похибки заокруглення.
Ітераційні
методи
(їх також називають
методами
послідовних
наближень)
полягають
у тому, що розв’язок
x
системи (1)
відшукується
як границя при
![]() послідовних
наближень
послідовних
наближень
![]() де
n-
номер
ітерації. Як
правило, за
скінченну
кількість
ітерацій ця
границя не
досягається.
де
n-
номер
ітерації. Як
правило, за
скінченну
кількість
ітерацій ця
границя не
досягається.
______________________
* Крамер Габрієль (1704-1752)- швейцарський математик.
** Гаус Карл Фридрих (1777-1855)- німецький математик, астроном, фізик, геодезист, професор Гетінгенського університету.
МЕТОД ГАУССА .
Запишемо систему (1) у розгорнутому вигляді:
а11x1+a12x2+...+a1mxm=f1 ,
a21x1+a22x2+...+a2mxm =f2 , (2)
......................................
am1x1+am2x2+...+ammxm =fm .
Метод Гаусса розв’язання системи (2) полягає у послідовному вилученні невідомих x1, x2, ..., xm-1 з цієї системи.
Припустимо,
що
a11![]() 0
. Поділив перше
рівняння на
a11,
одержимо
0
. Поділив перше
рівняння на
a11,
одержимо
x1+c12x2 +...+c1m xm =y1 , (3)
![]()
де : c1j=a1j /a11 ; j=2,m ; y1=f1/a11 .
Розглянемо тепер рівняння системи (2), що залишилися
![]()
ai1x1+ai2x2+...+aimxm=fi ; i= 2,m . (4)
![]() Помножимо
(3) на ai1
та віднімемо
одержане рівняння
з і-го рівняння
системи
(4),
i=2,m.
Помножимо
(3) на ai1
та віднімемо
одержане рівняння
з і-го рівняння
системи
(4),
i=2,m.
У результаті одержимо наступну систему рівнянь:
x1+c12x2+...+c1jxj+...+c1mxm =y1 ,
(1) (1) (1) (1)
a22x2+... +a2jxj+...+a2mxm=f2 ,
............................................ (5)
(1) (1) (1) (1)
am2x2+...+amjxj+...+ammxm=fm .
Tут позначено:
![]() (1)
(1)
(1)
(1)
aij=aij-c1jai1; fi=fi -y1ai1; i,j=2,m . (6)
Матриця системи (5) має вигляд:
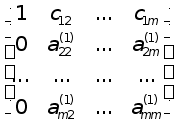 .
.
Матриці такої стуктури заведено позначати так:
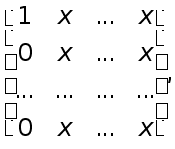
де хрестиками позначені ненульові елементи.
У системі (5) невідоме х міститься тільки в першому рівнянні, тому у подальшому достатньо мати справу із скороченою системою рівнянь:
(1) (1) (1) (1)
a22x2 +...+a2jxj +...+a2mxm =f2 ,
.............................................. (7)
(1) (1) (1) (1)
am2x2 +...+amjxj +...+ammxm =fm .
Тим
самим ми здійснили
перший крок
методу Гаусса
. Коли
![]() ,
то з системи
(7) зовсім аналогічно
можна вилучити
невідоме x2
і прийти до
системи, еквівалентній
(2),що має матрицю
такої структури:
,
то з системи
(7) зовсім аналогічно
можна вилучити
невідоме x2
і прийти до
системи, еквівалентній
(2),що має матрицю
такої структури:
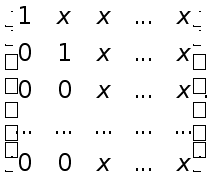
При цьому перше рівняння системи (5) залишається без зміни.
Вилучая таким же чином невідомі х 3, х4 ,... ,x m-1 , приходимо остаточно до системи рівнянь виду:
x1 +c12x2 +...+c1,m-1xm-1+c1mxm =y1,
x2 +...+c2,m-1xm-1+c2mxm =y2 ,
................................
xm-1+cm-1,mxm=ym-1,
xm=ym ,
що еквівалентна початковій системі (2) .
Матриця цієї системи
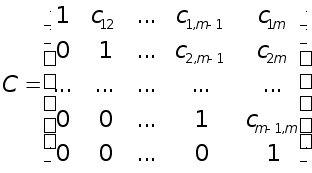
містить нулі усюди нижче головної діагоналі. Матриці такого виду називаються верхніми трикутними матрицями. Нижньою трикутною матрицею називається така матриця, у якої дорівнюють нулю усі елементи, що містяться вище головної діагоналі.
Побудова системи (8) складає прямий хід методу Гаусса. Зворотнiй хід полягає у відшуканні невідомих х1, ... ,хm з системи (8). Тому що матриця системи має трикутний вигляд, можна послідовно, починаючи з хm, відшукати всі невідомі. Дійсно, xm=ym,
x m-1 =ym-1 -cm-1,m x m i т. д.
Загальні форми зворотнього ходу мають вигляд:
m
![]() xi
=yi
- е
cijxj
; i=m-1,1; xm
=ym
.
(10)
xi
=yi
- е
cijxj
; i=m-1,1; xm
=ym
.
(10)
j=i+1
При реалізації на ЕОМ прямого ходу методу Гаусса немає необхідності діяти із змінними x1 ,x2 ,... ,xm. Досить вказати алгоритм,за яким початкова матриця А перетворюється до трикутного вигляду (9), та вказати відповідне перетворення правих частин системи.
Одержимо ці загальні формули.
Нехай вже здійснені перші к-1 кроків, тобто вже вилучені змінні
x1 , x2,..., xk-1 .
Тоді маємо систему:
x1+c12 x2 +...+c1,k-1xk-1+ c1kxk+....+c1mxm =y1 ,
x2 +...+c2,k-1xk-1+ c2kxk+....+c2mxm =y2 ,
..............................................
xk-1+ck-1,kxk+...+ck-1,mxm=yk-1 , (11)
(k-1) (k-1) (k-1)
akkxk+...+akmxm =fk ,
............................
(k-1) (k-1) (k-1)
amkxk+...+ammxm =fm .
Розглянемо К-те рівняння цієї системи:
(k-1) (k-1) (k-1)
akkxk+...+akmxm=fk ,
та
припустимо,
що
![]() . Поділивши
обидві частини
цього рівняння
на
. Поділивши
обидві частини
цього рівняння
на
![]() ,
одержимо
,
одержимо
xk+ck,k+1xk+1+...+ckmxm=yk , (12)
(k-1) (k-1) (k-1) (k-1)
де ckj=akj / akk ; j=k+1,m ; yk=fk / akk .
Далі
помножимо
рівняння (12) на
![]() та віднімемо
одержане
співвідношення
з
i-го
рівняння системи
(11). У результаті
остання група
рівнянь системи
(11) набуває наступного
вигляду:
та віднімемо
одержане
співвідношення
з
i-го
рівняння системи
(11). У результаті
остання група
рівнянь системи
(11) набуває наступного
вигляду:
x k+ck,k+1xk+1 +...+ ckmxm=yk,
(k) (k) (k)
ak+1,k+1xk+1+...+ ak+1,mxm=fk+1,
.......................................
(k) (k) (k)
am,k+1xk+1+... + ammxm=fm ,
![]()
![]() (k)
(k-1)
(k-1)
(k)
(k-1)
(k-1)
(k)
(k-1)
(k-1)
(k)
(k-1)
(k-1)
де: aij =aij - aikckj ; i,j=k+1,m ; fi= fi - aikyk ; i=k+1,m .
Таким чином, у прямому ході методу Гаусса коефіцієнти рівнянь перетворюються за наступним правилом
![]() (0)
(0)
akj =akj ; k,j=1,m ;
![]()
![]() (k-1)
(k-1)
(k-1)
(k-1)
ckj=akj /akk ; j=k+1,m ; k=1,m ; (13)
![]()
![]() (k)
(k-1) (k-1)
(k)
(k-1) (k-1)
aij =aij - aikckj ; i,j=k+1,m ; k=1,m . (14)
Обчислення правих частин системи (8) здійснюється за формулами:
![]() (0)
(k-1)
(k-1)
(0)
(k-1)
(k-1)
fk=fk ; yk = fk / akk ; k=1,m ; (15)
![]() (k)
(k-1) (k-1)
(k)
(k-1) (k-1)
fi = fi - aikyk ; k=1,m . (16)
![]()
![]()
Коефіціенти cij і праві частини yi ; i=1,m ; j=i+1,m зберігаються у пам’яті ЕОМ і використовуються при здійсненні зворотнього ходу за формулами (10).
Основним
обмеженням
методу є припущення,
що усі елементи
![]() ,
на які здійснюється
ділення, відрізняються
від нуля. Число
,
на які здійснюється
ділення, відрізняються
від нуля. Число
![]() називається
провідним
елементом на
К-му
кроці вилучення.
Навіть,
якщо деякий
провідний
елемент не
дорівнює нулеві,
а просто є близьким
до нуля, в процесі
обчислень може
мати місце
нагромадження
похибок. Вихід
з цієї ситуації
полягає в тому,
шо як провідний
елемент вибирається
не
називається
провідним
елементом на
К-му
кроці вилучення.
Навіть,
якщо деякий
провідний
елемент не
дорівнює нулеві,
а просто є близьким
до нуля, в процесі
обчислень може
мати місце
нагромадження
похибок. Вихід
з цієї ситуації
полягає в тому,
шо як провідний
елемент вибирається
не
![]() , а інше число
( тобто на
К-му
кроці вилучається
не xk,
а інша змінна
xj
,
, а інше число
( тобто на
К-му
кроці вилучається
не xk,
а інша змінна
xj
,
![]() )
.
Така
стратегія
вибору провідних
елементів
здійснюється
в методі Гаусса
з
вибором
головного
елементу, який
буде розглянуто
пізніш.
)
.
Така
стратегія
вибору провідних
елементів
здійснюється
в методі Гаусса
з
вибором
головного
елементу, який
буде розглянуто
пізніш.
А тепер підрахуємо число арифметичних дій, що необхідні для розв’язання системи за допомогою методу Гаусса. Оскільки виконання операцій множення і ділення на ЕОМ потребує набагато більше часу, ніж виконання додавання і віднімання, обмежимось підрахуванням числа множень і ділень.
1.Обчислення
коефіцієнтів
![]() за формулами
(13) потребує:
за формулами
(13) потребує:
![]() (m-k)=1+2+...+(m-1)=
(m-k)=1+2+...+(m-1)=
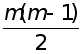 ділень
.
ділень
.
2.Обчислення
усіх коефіцієнтів
![]() за формулами
(14) потребує
за формулами
(14) потребує
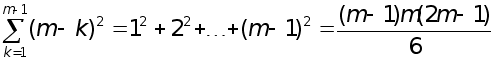
множень
(тут ми використовуємо
легко перевіряєму
за індукцією
рівність
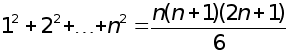 ).
).
Таким
чином, обчислення
ненульових
елементів
![]() трикутної
матриці С потребує
трикутної
матриці С потребує
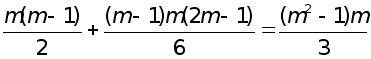
операцій множення і ділення.
3.Обчислення правих частин yk за формулами (15) потребує m
ділень,
а
відшукання
![]() за формулами
(16)
за формулами
(16)
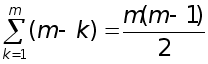
множень. Разом, обчислення правих частин перетвореної системи (8) потребує
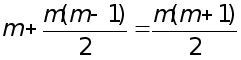
дій множення і ділення.
Усього для реалізації прямого ходу методу Гаусса необхідно виконати
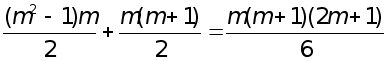
дій.
4.Для реалізації зворотнього ходу методу Гаусса за формулами (10) необхідно
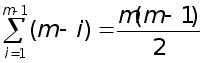
множень.
Всього, для реалізації методу Гаусса необхідно виконати
дій
множення і
ділення, причому
основний час
витрачається
на прямий хід.
Для великих
m
число
дій множення
і ділення у
методі Гаусса
близьке до
![]() За витратами
часу та необхідній
машинній пам’яті
метод Гаусса
придатний для
розв’язання
систем рівнянь
(2) загального
вигляду з кількістю
змінних
m порядку
100.
За витратами
часу та необхідній
машинній пам’яті
метод Гаусса
придатний для
розв’язання
систем рівнянь
(2) загального
вигляду з кількістю
змінних
m порядку
100.
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ .
Пусть
имеется функция
![]() которую необходимо
продифференцировать
несколько раз
и найти эту
производную
в некоторой
точке.
которую необходимо
продифференцировать
несколько раз
и найти эту
производную
в некоторой
точке.
Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно его заменить более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных ввобще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования.
Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции приближенного заменяется соответствующей производной интерполяционного многочлена
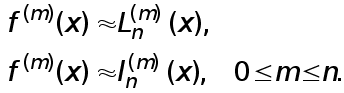
Рассмотрим простейшие формулы численного дифференцирования, которые получаются указанным способом.
Будем предполагать, что функция задана в равностоящих узлах
![]()
Ее
значения и
значения производных
в узлах будем
обозначать
![]()
Пусть
функция задана
в двух точках
![]() и
и
![]() ее значения
ее значения
![]()
Посстроим интерполяционный многочлен первой степени
![]()
Производная
![]() равна
равна
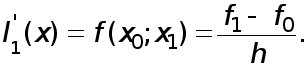
![]()
Производную
функцию
![]() в точке
в точке
![]() приближенно
заменяем производной
интерполяционного
многочлена
приближенно
заменяем производной
интерполяционного
многочлена
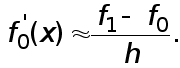 (1)
(1)
Величина
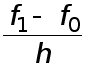 называется
первой
разностной
производной.
называется
первой
разностной
производной.
Пусть
![]() задана в трех
точках
задана в трех
точках
![]()
![]()
Интерполяционный многочлен Ньютона второй степени имеет вид
![]()
Берем производную
![]()
В точке
![]() она равна
она равна
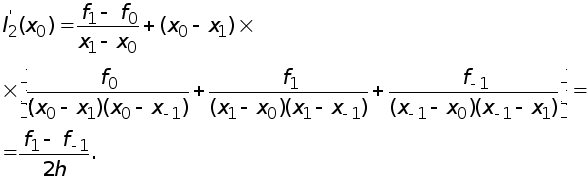
Получаем приближенную формулу
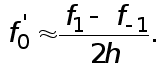 (2)
(2)
Величина
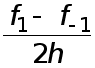 называется
центральной
разностной
производной.
называется
центральной
разностной
производной.
Наконец, если взять вторую производную
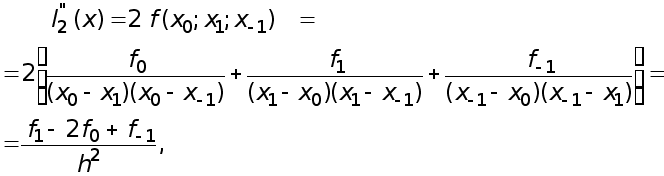 получаем
приближенную
формулу.
получаем
приближенную
формулу.
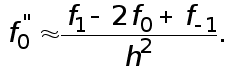 (3)
(3)
Величина
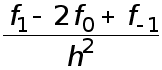 называется
второй
разностной
производной.
называется
второй
разностной
производной.
Формулы (1)-(3) называются формулами численного дифференцирования.
Предполагая
функцию
![]() достаточное
число раз непрерывно
дифференцируемой,
получим погрешности
приближенных
формул (1)-(3).
достаточное
число раз непрерывно
дифференцируемой,
получим погрешности
приближенных
формул (1)-(3).
В дальнейшем нам понадобится следующая лемма.
Лемма 1.
Пусть
![]() произвольные
точки,
произвольные
точки,
![]() Тогда существует
такая точка
Тогда существует
такая точка
![]() что
что
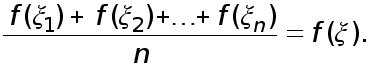
Доказательство. Очевидно неравенство
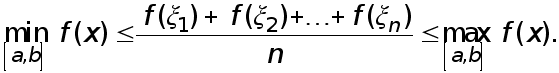
По теореме
Больцано-Коши
о промежуточных
значениях
непрерывной
функции на
замкнутом
отрезке она
принимает все
значения между
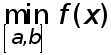 и
и
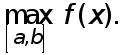 Значит существует
такая точка
Значит существует
такая точка
![]() что выполняет
указанное в
лемме равенство.
что выполняет
указанное в
лемме равенство.
Погрешности формул численного дифференцирования дает следующая лемма.
Лемма 2.
1.Предположим,
что
![]() Тогда существует
такая точка
Тогда существует
такая точка
![]() , что
, что
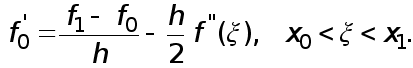 (4)
(4)
Если
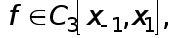 то существует
такая точка
то существует
такая точка
 , что
, что
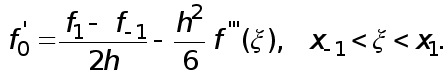 (5)
(5)
Когда
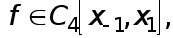 то существует
то существует
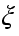 такая, что
такая, что
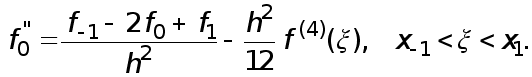 (6) Доказательство.
По формуле
Тейлора
(6) Доказательство.
По формуле
Тейлора
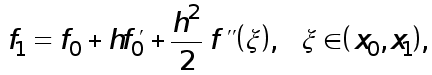
откуда следует (4).
Если
![]() то по формуле
Тейлора
то по формуле
Тейлора
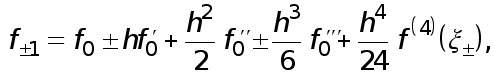 (7)
(7)
где
![]()
Подставим
(7) в
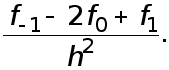 Получаем
Получаем
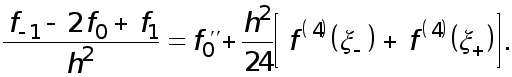
Заменяя в соответствии с леммою 1
![]()
получаем
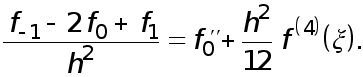
Откуда и следует (6).
Равенство (5) доказывается аналогично ( доказательство провести самостоятельно).
Формулы (4)-(6) называются формулами численного дифференцирования с остаточными членами.
Погрешности формул (1)-(3) оцениваются с помощью следующих неравенств, которые вытекают из соотношений (4)-(6):
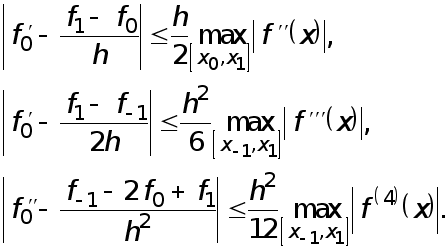
Говорят,
что погрешность
формулы (1) имеет
первый
порядок относительно
![]() (или порядка
(или порядка
![]() ), а погрешность
формул (2) и (3) имеет
второй
порядок относительно
), а погрешность
формул (2) и (3) имеет
второй
порядок относительно
![]() (или порядка
(или порядка
![]() ). Также говорят,
что формула
численного
дифференцирования
(1) первого
порядка точности
(относительно
). Также говорят,
что формула
численного
дифференцирования
(1) первого
порядка точности
(относительно
![]() ),
а формулы (2) и
(3) имеют второй
порядок точности.
),
а формулы (2) и
(3) имеют второй
порядок точности.
Указанным способом можно получать формулы численного дифференцирования для более старших производных и для большего количества узлов интерполирования.
Выбор
оптимального
шага. Допустим,
что граница
абсолютной
погрешности
при вычислении
функции
![]() в каждой точке
удовлетворяет
неравенству
в каждой точке
удовлетворяет
неравенству
![]() (8)
(8)
Пусть в
некоторой
окрестности
точки
![]() производные,
через которые
выражаются
остаточные
члены в формулах
(5), (6), непрерывны
и удовлетворяют
неравенствам
производные,
через которые
выражаются
остаточные
члены в формулах
(5), (6), непрерывны
и удовлетворяют
неравенствам
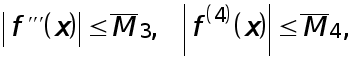 (9)
(9)
где
![]() - некоторые
числа. Тогда
полная погрешность
формул (2), (3) (без
учета погрешностей
округления)
в соответствии
с (5), (6), (8), (9)не превосходит
соответственно
величин
- некоторые
числа. Тогда
полная погрешность
формул (2), (3) (без
учета погрешностей
округления)
в соответствии
с (5), (6), (8), (9)не превосходит
соответственно
величин
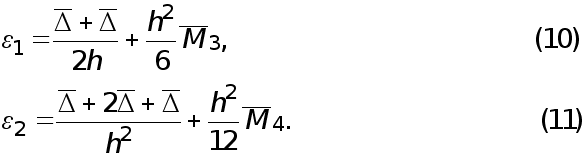
Минимизация
по
![]() этих величин
приводит к
следующим
значениям
этих величин
приводит к
следующим
значениям
![]() :
:
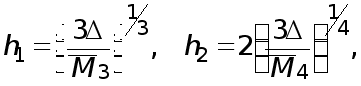 (12)
(12)
при этом
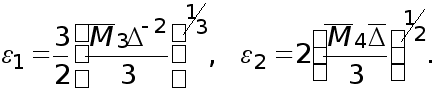 (13)
(13)
Если при
выбранном для
какой-либо из
формул (2), (3) значении
![]() отрезок
отрезок
![]() не выходит за
пределы окрестности
точки
не выходит за
пределы окрестности
точки
![]() ,
в которой выполняется
соответствующее
неравенство
(9), то найденное
,
в которой выполняется
соответствующее
неравенство
(9), то найденное
![]() есть оптимальным
и полная погрешность
численного
дифференцирования
оценивается
соответствующей
величиной (13).
есть оптимальным
и полная погрешность
численного
дифференцирования
оценивается
соответствующей
величиной (13).
ИНТЕРПОЛИРОВАНИЕ СПЛАЙНАМИ.
Интерполирование
многочленом
Лагранжа или
Ньютона на
отрезке
![]() с использованием
большого числа
узлов интерполяции
часто приводит
к плохому
приближению,
что объясняется
сильным накоплением
погрешностей
в процессе
вычислений.
Кроме
того
из-за расходимости
процесса интерполяции
увеличение
числа узлов
не обязано
приводить к
повышению
точности.
Для того, чтобы
избежать больших
погрешностей,
весь отрезок
с использованием
большого числа
узлов интерполяции
часто приводит
к плохому
приближению,
что объясняется
сильным накоплением
погрешностей
в процессе
вычислений.
Кроме
того
из-за расходимости
процесса интерполяции
увеличение
числа узлов
не обязано
приводить к
повышению
точности.
Для того, чтобы
избежать больших
погрешностей,
весь отрезок
![]() разбивают на
частичные
отрезки и на
каждом из частичных
отрезков приближенно
заменяют функцию
разбивают на
частичные
отрезки и на
каждом из частичных
отрезков приближенно
заменяют функцию![]() многочленом
невысокой
степени ( так
называемая
кусочно-полиномиальная
интерполяция).
многочленом
невысокой
степени ( так
называемая
кусочно-полиномиальная
интерполяция).
Одним
из способов
интерполяции
на всем отрезке
является
интерполирование
с помощью
сплайн-функций.
Сплайн-функцией
или сплайном
называют
кусочно-полиномиальную
функцию, определенную
на отрезке
![]() и имеющую на
этом отрезке
некоторое число
непрерывных
производных.
и имеющую на
этом отрезке
некоторое число
непрерывных
производных.
Слово ,,сплайн’’ (английское spline) означает гибкую линейку, используемую для проведения гладких кривых через заданные точки плоскости.
Преимущество сплайнов перед обычной интерполяцией является, во-первых, их сходимость, и, во-вторых, устойчивость процесса вычислений.
Рассмотрим частный, но распространенный в вычислительной практике случай, когда сплайн определяется с помощью многочленов третьей степени ( кубический сплайн).
Пусть
на
![]() задана непрерывная
функция
задана непрерывная
функция![]() .
Введем узлы
( сетку):
.
Введем узлы
( сетку):
![]()
и обозначим
![]()
Интерполяционным
кубическим
сплайном,
соответствующим
данной функции
![]() и данным узлам,
называеться
функция
и данным узлам,
называеться
функция
![]() ,
удовлетворяющая
следующим
усовиям:
,
удовлетворяющая
следующим
усовиям:
а) на кождом
сегменте
![]() функция
функция
![]() является многочленом
третьей степени;
является многочленом
третьей степени;
б) функция
![]() ,
а так же ее первая
и вторая производные
непрерывны
на
,
а так же ее первая
и вторая производные
непрерывны
на
![]() ;
;
в)
![]()
Последнее условие называется условием интерполирования.
Докажем существование и единственность сплайна, определяемого перечисленными условиями (плюс некоторые граничные условия, которые будут введены в процессе доказательства). Приводимое ниже доказательство содержит также способ построения сплайна.
На каждом
из отрезков
![]() будем искать
функцию
будем искать
функцию
![]() в виде многочлена
третьей степени
в виде многочлена
третьей степени
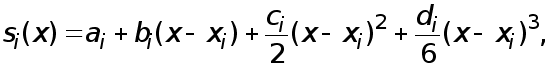 (1)
(1)
![]()
где
![]() - коэффициенты,
подлежащие
определению.
Выясним смысл
введенных
коэффициентов.
Имеем
- коэффициенты,
подлежащие
определению.
Выясним смысл
введенных
коэффициентов.
Имеем
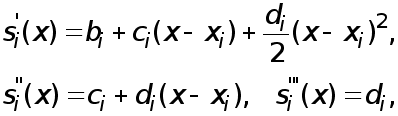
поэтому ![]()
Из условий
интерполирования
![]() получаем, что
получаем, что
![]()
Доопределим
, кроме того ,
![]() .
.
Далее
, требование
непрерывности
функции
![]() приводит к
условиям
приводит к
условиям
![]()
Отсюда,учитывая
выражения для
функций
![]() получаем при
получаем при
![]() уравнения
уравнения
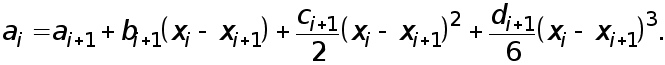 Обозначая
Обозначая
![]() перепишем эти
уравнения в
виде
перепишем эти
уравнения в
виде
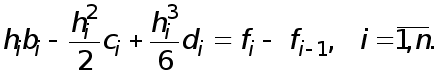 (2)
(2)
Условия непрерывности первой производной
![]()
приводят к уравнениям
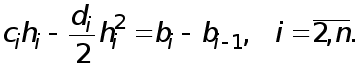 (3)
(3)
Из условий непрерывности второй производной получаем уравнения
![]() .
(4)
.
(4)
Объединяя
(2) -(4) , получим систему
![]() уравнений
относительно
уравнений
относительно
![]() неизвестных
неизвестных
![]()
Два недостающих
условия получают,
задавая те или
иные граничные
условия для
![]() Предположим,
например, что
функция
Предположим,
например, что
функция
![]() удовлетворяет
условиям
удовлетворяет
условиям
![]() Тогда естественно
требовать,
чтобы
Тогда естественно
требовать,
чтобы
![]() Отсюда получаем
Отсюда получаем
![]()
т.е.
![]()
Заметим,
что условие
![]() совпадает с
уравнением
(4) при
совпадает с
уравнением
(4) при
![]()
![]() .
Таким образом,
приходим к
замкнутой
системе уравнений
для определения
коэффициентов
кубического
сплайна:
.
Таким образом,
приходим к
замкнутой
системе уравнений
для определения
коэффициентов
кубического
сплайна:
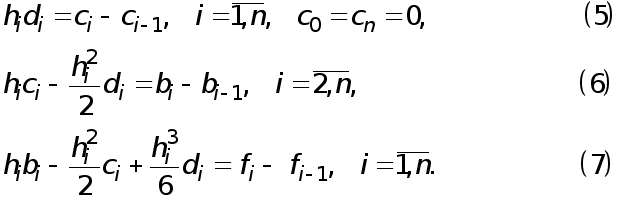 Убедимся
в том, что эта
система имеет
единственное
решение. Исключим
из (5)- (7) переменные
Убедимся
в том, что эта
система имеет
единственное
решение. Исключим
из (5)- (7) переменные
![]() и получим систему,
содержащую
только
и получим систему,
содержащую
только
![]() Для этого рассмотрим
два соседних
уравнения (7) :
Для этого рассмотрим
два соседних
уравнения (7) :
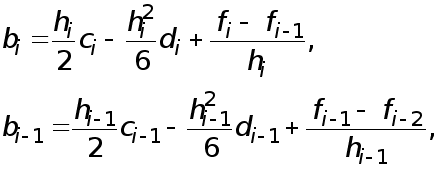
и вычтем второе уравнение из первого. Тогда получим
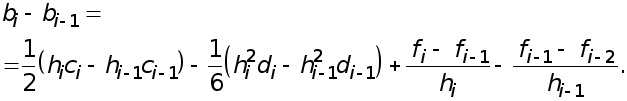
Подставляя
найденное
выражение для
![]() в правую часть
уравнения (6),
получим
в правую часть
уравнения (6),
получим
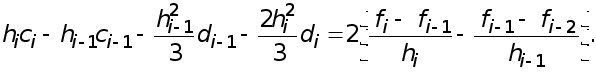 (8)
(8)
Далее, из уравнения (5) получаем
![]()
И подставляя эти выражения в (8) , приходим к уравнению
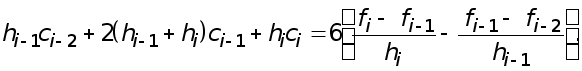
Окончательно
для определения
коэффициентов
![]() получаем систему
уравнений
получаем систему
уравнений
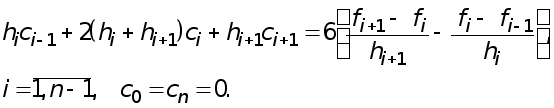 (9)
(9)
В силу
диагонального
преобладания
система (9) имеет
единственное
решение. Так
как матрица
системы трехдиагональная,
решение можно
найти методом
прогонки. По
найденным
коэффициентам
![]() коэффициенты
коэффициенты
![]() і
і
![]() определяются
с помощь явных
формул
определяются
с помощь явных
формул
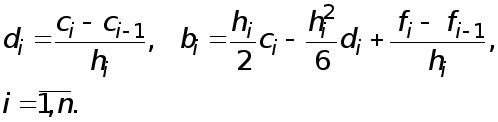 (10)
(10)
Таким
образом, доказано,
что существует
единственный
кубический
сплайн, определяемый
условиями
а)-в) и граничными
условиями
![]() Заметим , что
можно рассматривать
и другие граничные
условия.
Заметим , что
можно рассматривать
и другие граничные
условия.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.
На практике редко удается вычислить точно определенный интеграл. Например, в элементарных функциях не вычисляется функция Лапласа
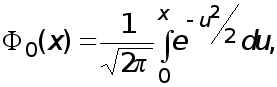
широко используемая в теории вероятностей для вычисления вероятностей, связанных с нормально распределенными случайными величинами.
Рассмотрим некотрые широко используемые приемы приближенного вычисления определенных интегралов.
Квадратурные формулы.
Введем понятие квадратурные формулы. Пусть дан определенный интеграл
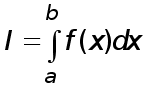 (1)
(1)
от непрерывной
на отрезке
![]() функции
функции
![]() . Приближенное
неравенство
. Приближенное
неравенство
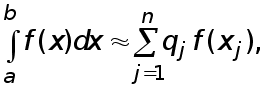 (2)
(2)
где
![]() - некоторые
числа,
- некоторые
числа,
![]() - некотрые точки
отрезка
- некотрые точки
отрезка
![]() , называется
квадратурной
формулой,
определяемой
весами
, называется
квадратурной
формулой,
определяемой
весами
![]() и узлами
и узлами
![]() .
.
Говорят, что
квадратурная
формула точна
для многочленов
степени
![]() , если при замене
, если при замене
![]() на произвольный
алгебраический
многочлен
степени
на произвольный
алгебраический
многочлен
степени
![]() приближенное
равенство (2)
становится
точным.
приближенное
равенство (2)
становится
точным.
Рассмотрим наиболее простые квадратурные формулы.
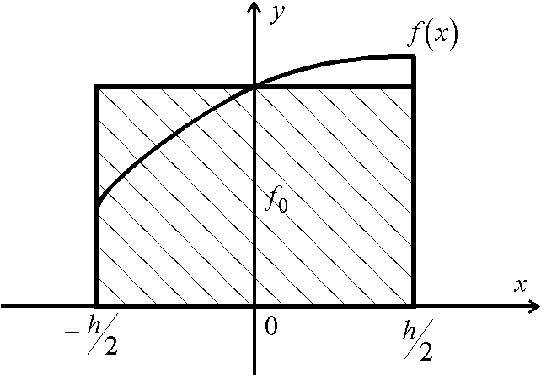
Формула
прямоугольников.
Допустим, что
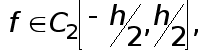
![]() . Положим приближенно
. Положим приближенно
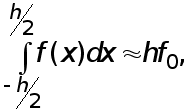 (3)
(3)
где
![]() ,
т.е. площадь
криволинейной
трапеции,
ограниченной
сверху графиком
функции
,
т.е. площадь
криволинейной
трапеции,
ограниченной
сверху графиком
функции
![]() ,
аппроксимируется
площадью
прямоугольника,
высота которого
равна значению
,
аппроксимируется
площадью
прямоугольника,
высота которого
равна значению
![]() в средней точке
основания
трапеции .
в средней точке
основания
трапеции .
Найдем остаточный член , т.е. погрешность формулы (3) .
Пусть
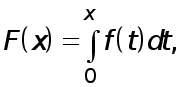 (4)
(4)
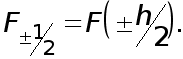 Так как
Так как
![]()
![]() то согласно
формуле Тейлора
с остаточным
членом в форме
Лагранжа имеем
то согласно
формуле Тейлора
с остаточным
членом в форме
Лагранжа имеем
![]()
 (5)
(5)
где
![]() -некоторые
точки ,
-некоторые
точки ,
![]()
Функция
![]() является
первообразной
для
является
первообразной
для
![]() Поэтому для
интеграла,
стоящего в
левой части
приближенного
равенства (3),
из формулы
Ньтона - Лейбница
с расчетом (5)
вытекает следующее
соотношеие
Поэтому для
интеграла,
стоящего в
левой части
приближенного
равенства (3),
из формулы
Ньтона - Лейбница
с расчетом (5)
вытекает следующее
соотношеие
Отсюда с помощью ранее доказанной леммы получаем формулу прямоугольников с остаточным членом :
 (6)
(6)
Формула
трапеций.
Пусть
![]() Полагаем
Полагаем
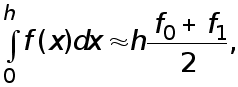 (7)
(7)
где
![]() т.е. интеграл
т.е. интеграл
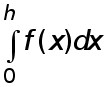 приближенно
заменяется
площадью
заштрихованной
трапеции, показанной
на рисунке.
приближенно
заменяется
площадью
заштрихованной
трапеции, показанной
на рисунке.
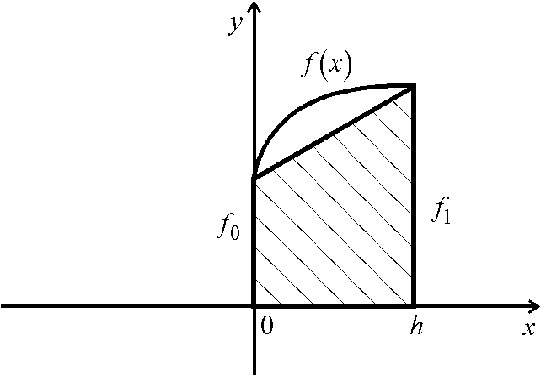
Найдем
остаточный
член, т.е. погрешность
формулы (7). Выразим
![]() і
і
![]() где
где
![]() - функция (4), по
формуле Тейлора
с остаточным
членом в интегральной
форме
- функция (4), по
формуле Тейлора
с остаточным
членом в интегральной
форме
![]() :
:
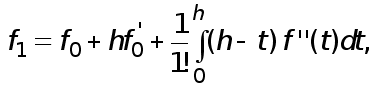 (8)
(8)
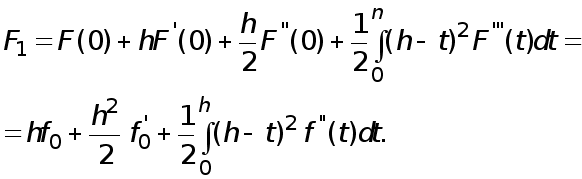 (9)
(9)
Согласно (8) имеем
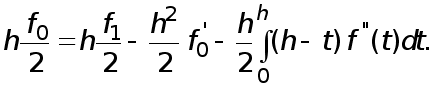 (10)
(10)
Отделив
в правой части
(9) слагаемое
![]() и заменив его
выражением
(10), с учетом того,
что
и заменив его
выражением
(10), с учетом того,
что
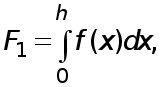 находим
находим
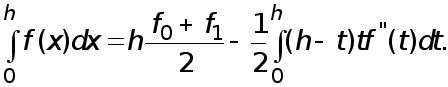
![]()
Преобразуем теперь второе слагаемое в правой части, используя обобщенную теорему о среднем.
![]()
* Формула Тейлора с остаточным членом в интегральной форме
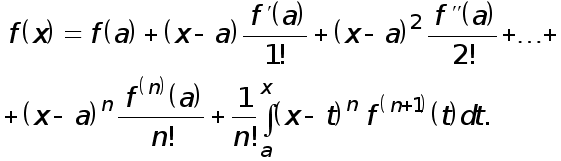
Теорема
1 (обобщенная
теорема о среднем).
Пусть
![]() причем
причем
![]() на
на
![]() Тогда существует
такая точка
Тогда существует
такая точка
![]() что
что
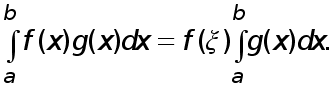
Доказательство. Положим
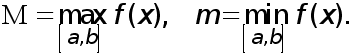 (11)
(11)
Тогд, так
как
![]() то
то
![]()
и, следовательно,
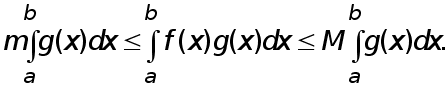
![]()
Если
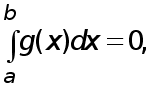 то
то
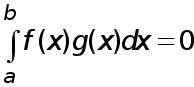 и в качестве
и в качестве
![]() можн взять
любую точку
из
можн взять
любую точку
из
![]()
Если
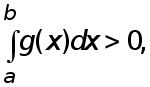 то вытекает
существование
такого числа
с,
удовлетворяющего
неравенствам
( для этого делим
все части
то вытекает
существование
такого числа
с,
удовлетворяющего
неравенствам
( для этого делим
все части
![]() на
на
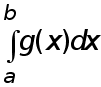 ):
):
![]() (12)
(12)
что
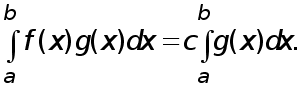 (13)
(13)
По теореме
о промежуточных
значениях
непрерывной
функции в силу
(11) , (12) найдется
точка
![]() , в которой
, в которой
![]() что вместе с
равенством
(13) доказывает
теорему .
что вместе с
равенством
(13) доказывает
теорему .
Теперь,
так как
![]() то по доказанной
теоремою
то по доказанной
теоремою
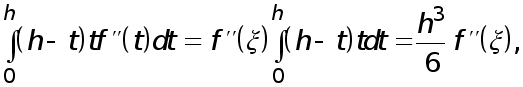
где
![]() - некоторая
точка . Подставляя
полученное
в
- некоторая
точка . Подставляя
полученное
в
![]() ,
приходим к
формуле
трапеций с
остаточным
членом :
,
приходим к
формуле
трапеций с
остаточным
членом :
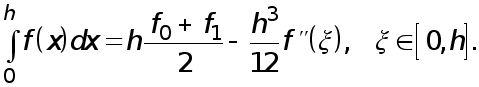 (14)
(14)
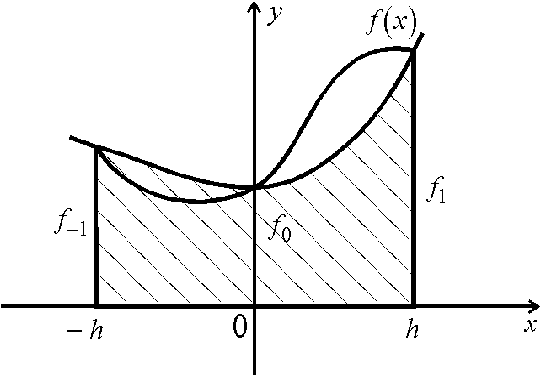
Формула
Симпсона .
Предположим,
что
![]() Интеграл
Интеграл
 приближенного
заменяем площадью
заштрихованной
криволинейной
трапеции,
ограниченной
сверху параболой,
проходящей
через точки
приближенного
заменяем площадью
заштрихованной
криволинейной
трапеции,
ограниченной
сверху параболой,
проходящей
через точки
![]() де
де
![]()
Указанная парабола задается уравнением
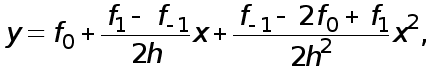
в чем
нетрудно убедиться,
положив поочередно
![]()
![]() (ее можно также
получить, построив
интерполяционный
многочлен
второй степени
и приводя подобные
) Отсюда находи
( проверить
самостоятельно)
(ее можно также
получить, построив
интерполяционный
многочлен
второй степени
и приводя подобные
) Отсюда находи
( проверить
самостоятельно)
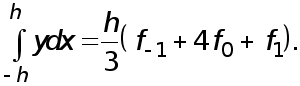
Таким образом , формула Симпсона , называемая также формулой парабол , имеет вид
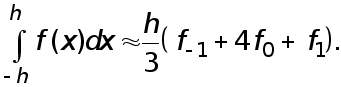 (15)
(15)
Положим
![]() где
где
![]() -функция
(4). Поскольку
-функция
(4). Поскольку
![]()
то согласно формул Тейлора с остаточным членом в интегральной форме имеем
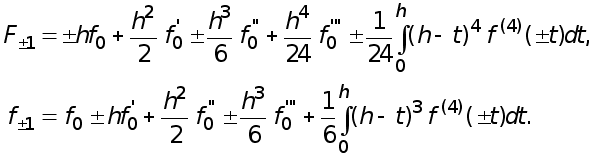 Отсюда
получаем
Отсюда
получаем
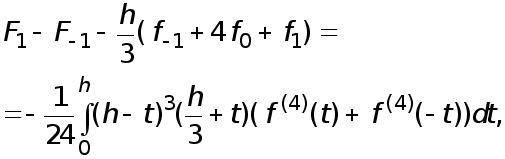 (16)
(16)
т.к. остальные члены взаимно уничтожаются.
Поскольку
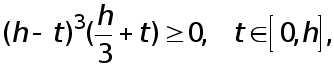 то применяя
к интегралу
(16) теорему 1 , а
затем к полученному
результату
лемму, находим
то применяя
к интегралу
(16) теорему 1 , а
затем к полученному
результату
лемму, находим
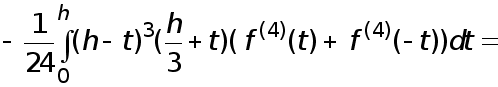
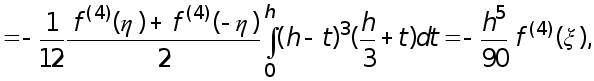 (17)
(17)
где
![]() нектрые точки.
нектрые точки.
Принимая
во внимание,
что
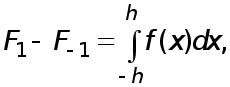 из (16), (17) приходим
к формуле
из (16), (17) приходим
к формуле
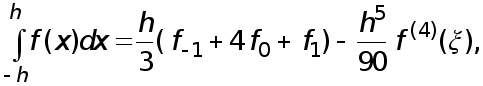 (18) т.е. к формуле
Симпсона с
остаточным
членом.
(18) т.е. к формуле
Симпсона с
остаточным
членом.
Рассмотрим квадратурные формулы прямоугольников (3), трапеций (7) и Симпсона (15) называются каноничными.
Усложненные квадратурные формулы.
На практике,
если требуется
вычислить
приближенно
интеграл (1) , обычно
делят заданный
отрезок
![]() на
на
![]() равных частей
и на кождом
частичном
отрезке применяют
какую-либо одну
каноничную
квадратурную
формулу, а затем
суммируют
полученные
результаты.
Построенная
таким путем
квадратурная
формула на
отрезке
равных частей
и на кождом
частичном
отрезке применяют
какую-либо одну
каноничную
квадратурную
формулу, а затем
суммируют
полученные
результаты.
Построенная
таким путем
квадратурная
формула на
отрезке
![]() называется
усложненной.
При применении
формул прямугольников
и трапеций
длину частичных
отрезков удобно
применять за
называется
усложненной.
При применении
формул прямугольников
и трапеций
длину частичных
отрезков удобно
применять за
![]() , а при использовании
формулы Симпсона
- за
, а при использовании
формулы Симпсона
- за
![]() .
.
Остановимся
сначала на
применении
формулы прямоугольников.
Пусть
![]() Обозначим
частичные
отрезки через
Обозначим
частичные
отрезки через
![]()
где
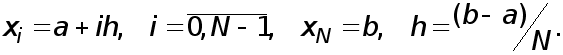
В соответствии с (3) полагаем
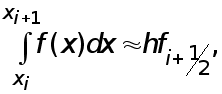 (19)
(19)
где
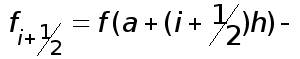 значение
значение
![]() в середине
частичного
отрезка
в середине
частичного
отрезка
![]() .
При этом справедливо
аналогичное
(6) равенство
.
При этом справедливо
аналогичное
(6) равенство
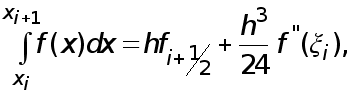 (20)
где
(20)
где
![]() некоторая
точка.
некоторая
точка.
Суммирование по всем частичным отрезкам приближенного равенства (19) приводит к усложненной квадратурной формуле прямоугольников:
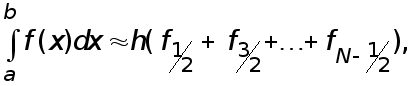 (21)
(21)
а суммирование равенств (20) с учетом того,что по лемме
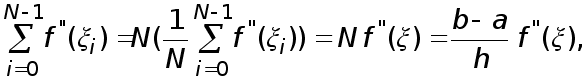
где
![]() -некоторая
точка отрезка
-некоторая
точка отрезка
![]() ,
дает усложненную
формулу прямоугольников
с остаточным
членом:
,
дает усложненную
формулу прямоугольников
с остаточным
членом:
![]()
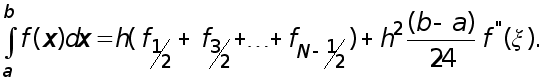 (22)
(22)
![]() Совершенно
аналогично
при
услвии, что
Совершенно
аналогично
при
услвии, что
![]() с использованием
формул (7), (14) получается
усложненная
квадратурная
формула трапеций
с использованием
формул (7), (14) получается
усложненная
квадратурная
формула трапеций
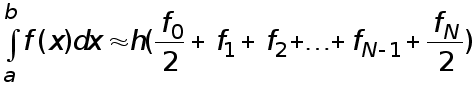 (23)
(23)
и отвечающая ей формула с остаточным членом
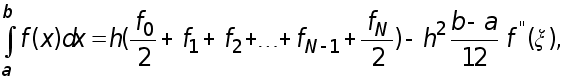 (24)
(24)
где
![]() некоторая
точка.
некоторая
точка.
Пусть
теперь
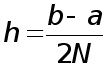 и, как обычно,
и, как обычно,
![]()
![]() Перепишем
каноническую
квадратурную
формулу Симпсона
(15) применительно
к отрезку
Перепишем
каноническую
квадратурную
формулу Симпсона
(15) применительно
к отрезку
![]() длины
длины
![]() :
:
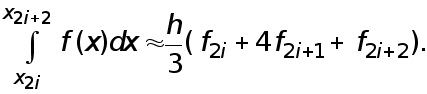
Суммируя левую и правую части этого соотношения от 0 до
N-1, получаем усложненную квадратурную формулу Симпсона (25)
Сответствующая
ей формула с
остаточным
членом, полученная
суммированием
по частичным
отрезкам
![]() равенств вида
(18), при условии,
что
равенств вида
(18), при условии,
что
![]() ,
такова :
,
такова :
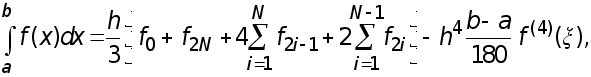 (26)
(26)
где
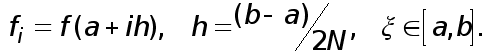
Введем краткие обозначения
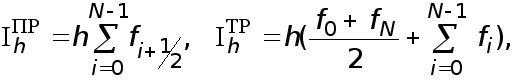 (27)
(27)
где
![]() а также положим
а также положим
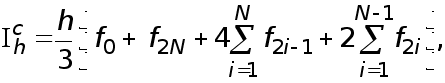 (28)
(28)
где
![]()
Приближенные равенства
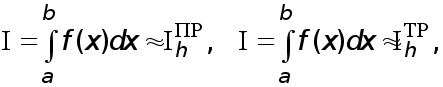 (29)
(29)
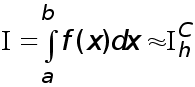 (30)
(30)
назовем сответственно формулами прямоугольников, трапеций и формулой Симпсона, опуская слова ‘’усложненная квадратурная’’.
Из виражений
остаточных
членов в (22), (24), (26)
видно, что формулы
(29) прямоугольников
трапеций точны
для многочленов
первой степени,
т.е. для линейных
функций, а формула
(30) Симпсона точна
для многочленов
третьей степени
(для них остаточный
член равен нулю
). Погрешность
формул (29) имеет
второй порядок
относительно
![]() (заведомо не
лучше, если
(заведомо не
лучше, если
![]() непрерывна
на
непрерывна
на
![]() и не обращается
в нуль), а формула
Симпсона при
соответствующей
гладкости
и не обращается
в нуль), а формула
Симпсона при
соответствующей
гладкости
![]() является формулой
четвертого
порядка точности.
Поэтму для
функций класса
является формулой
четвертого
порядка точности.
Поэтму для
функций класса
![]() при малом
при малом
![]() формула Симпсона
обычно дает
более высокую
точность, чем
формула (29).
формула Симпсона
обычно дает
более высокую
точность, чем
формула (29).
Погрешность формулы прямугольников и формулы Симпсона при вычислении интеграла (1) в силу (22), (26) удовлетворяет неравенствам
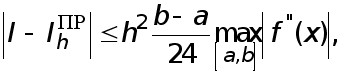 (31)
(31)
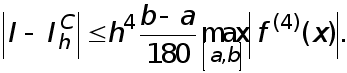 (32)
(32)
Аналогичное неравенство имеет место и для погрешности формули трапеций.
Наряду с оценками погрешноси сверху полезны оценки снизу. В частности, для погрешности формулы прямоугольников оценка снизу, вытекающая из (22), такова:
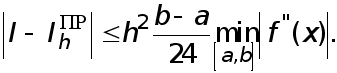 (33)
(33)
Пример. Исследовать погрешность квадратурных формул для интеграла
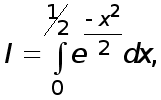 при
при
![]() .
.
Имеем
о
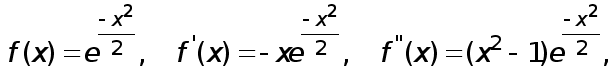
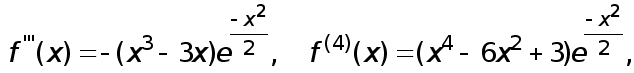
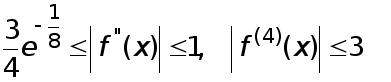 на
на
![]()
Согласно (31)-(33) получаем
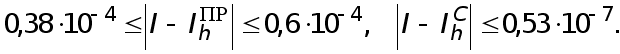
Формулы
прямоугольников
трапеций в
отдельности
уступают при
интегрировании
гладких функций
формуле Симпсона.
Однако в паре
они обладают
ценным качеством,
а именно, если
![]() не изменяет
знака на
не изменяет
знака на
![]() то формулы (29)
дают двусторонние
приближения
для интеграла
(1), так как согласно
(22), (24) их остаточные
члены имеют
противоположные
знаки.
то формулы (29)
дают двусторонние
приближения
для интеграла
(1), так как согласно
(22), (24) их остаточные
члены имеют
противоположные
знаки.
В рассмотренном
примере
![]() Поэтому
Поэтому
![]()
В данной
ситуации естественно
положить
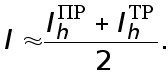
Тогда
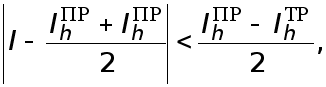 т.е. погрешность
оценивается
через самые
приближенные
значения интеграла.
т.е. погрешность
оценивается
через самые
приближенные
значения интеграла.
УМОВИ ЗАСТОСУВАННЯ МЕТОДУ ГАУССА.
Раніш було показано, що метод Гаусса перетворює вихідну систему рівнянь
![]() (1)
(1)
до еквівалентної системи
![]() , (2)
, (2)
де С- верхня трикутна матриця з одиницями на головнїй діагоналі. З’ясуємо тепер, як зв’язанi між собою вектори правих частин f та y.
Раніш ми переконалися, що праві частини системи (2) обчислюються за формулами
![]()
![]() ,
,
З цих співвідношень можна послідовно одержати
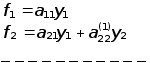
![]() , (3)
, (3)
де
![]() -числові
коефіцієнти,
причому
-числові
коефіцієнти,
причому
![]() .
.
Співвідношення (3) можна записати у матричному вигляді
![]() , (4)
, (4)
де B
-нижня трикутна
матриця з елементами
![]() на головній
діагоналі.
на головній
діагоналі.
Нагадаємо,
що головне
припущення
при формуліровці
методу Гаусса
полягало у
тому, що усі
![]() Тому на діагоналі
матриці В
стоять ненульові
елементи,
Тому на діагоналі
матриці В
стоять ненульові
елементи,
![]() ,
тобто
В має
обернену, a
,
тобто
В має
обернену, a
![]() .
Підставляючи
останнє у (2),
приходимо до
рівняння
.
Підставляючи
останнє у (2),
приходимо до
рівняння
![]()
звідки
![]() .
(5)
.
(5)
Порівнюючи (5) з рівнянням (1), приходимо до висновку, що як наслідок застосування методу Гаусса одержане розкладання вихідної матриці А у добуток A=BC , де В- нижня трикутна матриця з ненульовими елементами на головній діагоналі, С-верхня трикутна матриця з одиничною головною діагоналлю.
Зараз
можно тлумачити
метод Гаусса
таким чином.
Нехай задано
матрицю A
і вектор
f.
Спочатку утворюється
розклад А
у добуток двох
трикутних
матриць
![]() .
Далі послідовно
розв’язуються
дві системи
рівнянь
.
Далі послідовно
розв’язуються
дві системи
рівнянь
![]() (6)
(6)
![]() (7)
(7)
з трикутними матрицями, звідки і одержується шуканий вектор x. Розклад А=ВС відповідає прямій ході методу Гаусса, а розв’язання системи (6)- (7)- зворотній ході. Зауважимо, що у наведеному раніш алгоритмі розклад A=BC та розв’язання системи (6) провадиться одночасно.
Водночас з сказаного можна зробити наступний висновок. Тому що
![]() ,
,
то метод Гаусса дозволяє одночасно з ров’язаннням системи (1) обчислити визначник матриці А простим множенням ведучих елементів. Коли ж задачею є просто обчислення визначника матриці, то це можна зробити методом Гаусса, при цьому немає необхідності обчислювати праві частини перетворюємих рівнянь.
Далі, додержуючись стандартних позначень, нижні трикутні матриці будемо позначати L (від англійського lower- нижній), та верхні трикутні - літерою U (від англійського upper-верхній).
Позначимо
через
![]() -кутовий
мінор порядку
j матриці
А, тобто
-кутовий
мінор порядку
j матриці
А, тобто
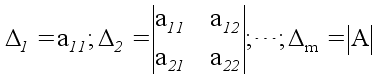 .
.
Теоретичне обгрунтування можливості розкладу матриці у добуток двох трикутних матриць містить наступна теорема.
Теорема
про LU-
розклад.
Нехай усі кутові
мінори матриці
А
відмінні від
нуля,
![]() .
Тоді матрицю
А
можна подати
єдиним чином
у вигляді добутка
.
Тоді матрицю
А
можна подати
єдиним чином
у вигляді добутка
А=LU , (8)
де L- нижня трикутна матриця з ненульовими діагональними елементами і U -верхня трикутна матриця з одиничною головною діагоналлю.
Доведення. Доведемо сформульоване твердження спочатку для матриць другого порядку. Будемо шукати розклад матриці
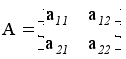
у вигляді
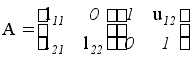 ,
,
де
![]() -
невідомі досі
числа. Для відшукання
цих чисел маємо
систему рівнянь:
-
невідомі досі
числа. Для відшукання
цих чисел маємо
систему рівнянь:
![]() ,
,
яка має єдиний розвязок
![]() .
.
За припущенням
теореми
![]() ,
тобто елементи
,
тобто елементи
![]() та
та
![]() відмінні від
нуля.
відмінні від
нуля.
Подальше
доведення
проведемо
методом математичної
індукції. Нехай
твердження
вірне для матриць
порядку
![]() доведемо,
що воно вірне
і для матриць
порядку к.
доведемо,
що воно вірне
і для матриць
порядку к.
Подамо матрицю А порядку К у вигляді
![]()
![]()
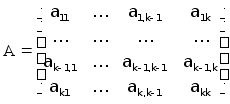 (9)
(9)
та позначимо
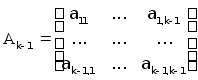 ;
;
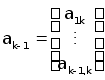 ,
,
![]() .
.
Згідно
з умовами теореми
![]() і тоді за припущеннями
індукції існує
розклад матриці
і тоді за припущеннями
індукції існує
розклад матриці
![]() ;
;
![]()
де
![]() -відповідно
нижня і верхня
трикутні матриці,
що володіють
вказаними у
теоремі властивостями.
Будемо шукати
розклад матриці
(9) у вигляді
-відповідно
нижня і верхня
трикутні матриці,
що володіють
вказаними у
теоремі властивостями.
Будемо шукати
розклад матриці
(9) у вигляді
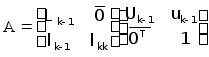 ,
(10)
,
(10)
де
![]() -
невідомі досі
вектори.
-
невідомі досі
вектори.
Помножимо матриці в правій частині рівняння (10) і, враховуючи (9), приходимо до системи рівнянь
![]() ; (11)
; (11)
![]() ; (12)
; (12)
![]() ; (13)
; (13)
З припущенння
індукції виходить
існування
матриць
![]() ;
;![]() .
Тому з (11) і (12) одержуємо
.
Тому з (11) і (12) одержуємо
![]() ;
;
![]()
і,далі, з (13)
![]() .
.
Таким
чином,![]() -розклад
матриці А існує.
З розкладу (10)
виходить, що
-розклад
матриці А існує.
З розкладу (10)
виходить, що
![]() .
.
За умовами
теореми
![]() ,
а за припущеннями
індукції
,
а за припущеннями
індукції
![]() ,
і тому
,
і тому
![]() .
Тим самим індукція
завершена і
доведена можливість
шуканого розкладу.
.
Тим самим індукція
завершена і
доведена можливість
шуканого розкладу.
Доведемо тепер, що такий розклад єдиний. Припустимо, що матрицю А можна розкласти двома способами
![]() .
.
Тоді
![]() i
i
![]() . (14)
. (14)
Матриця
у лівій частині
рівняння (14) є
верхньою трикутною,
а в правій частині
- нижньою трикутною.
Така рівність
можлива лише
у випадку. якщо
матриці
![]() і
і
![]() діагональні.
Але на діагоналі
матриці
діагональні.
Але на діагоналі
матриці
![]() (а тому і матриці
(а тому і матриці
![]() )
стоять одиниці,
отже ці матриці
одиничні
)
стоять одиниці,
отже ці матриці
одиничні
![]() .
.
Звідси
одержуємо
![]() ;
;![]() ,тобто розклад
(8) єдиний. Теорема
повністю доведена.
,тобто розклад
(8) єдиний. Теорема
повністю доведена.
Зауважимо,
що коли хоча
б один з углових
мінорів матриці
А
дорівнював
нулеві, то вказаний
![]() - розклад неможливий.
Це легко побачити
на прикладі
матриць другого
порядку.
- розклад неможливий.
Це легко побачити
на прикладі
матриць другого
порядку.
Висновок. Метод Гаусса можливо використовувати тоді, та й лише тоді, коли усі кутові мінори матриці А відмінні від нуля.
Було показано, що метод Гаусса приводить до розкладу вихідної матриці у добуток двох трикутних. Більш детально описати структуру цих трикутних матриць можливо за допомогою так званих елементарних трикутних матриць.
Матриця
![]() називається
елементарною
нижньою
трикутною
матрицею,
якщо вона має
вигляд
називається
елементарною
нижньою
трикутною
матрицею,
якщо вона має
вигляд
![]()
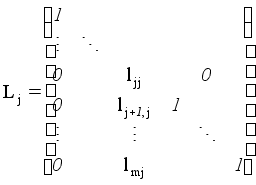 .
.
У матриці
![]() усі елементи
головної діагоналі
окрім
усі елементи
головної діагоналі
окрім
![]() дорівнюють
одиниці. З решти
елементів
відмінними
від нуля можуть
бути лише елементи
дорівнюють
одиниці. З решти
елементів
відмінними
від нуля можуть
бути лише елементи
![]() -го
стовпчика, що
розташовані
нижче
-го
стовпчика, що
розташовані
нижче
![]() .
Оберненою до
.
Оберненою до
![]() є елементарна
нижня трикутна
матриця
є елементарна
нижня трикутна
матриця
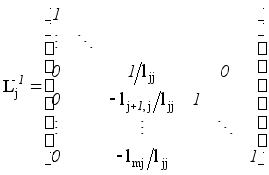 .
.
Розглянемо
спочатку для
наочності
систему
![]() ,
що складається
з трьох рівнянь:
,
що складається
з трьох рівнянь:
![]() ,
,
![]() , (15)
, (15)
![]() .
.
Після першого кроку виключення за методом Гаусса перетворена система приймає вигляд
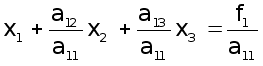 ,
,
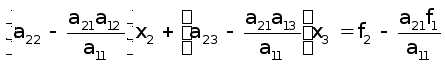 , (16)
, (16)
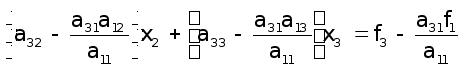 .
.
Звідси
видно, що матриця
![]() системи (16) одержується
з вихідної
матриці А
шляхом множення
А
зліва на елементарну
матрицю
системи (16) одержується
з вихідної
матриці А
шляхом множення
А
зліва на елементарну
матрицю
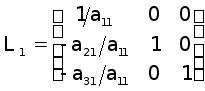 (17)
(17)
так, що
![]() .При
цьому систему
(16) можна записати
у вигляді
.При
цьому систему
(16) можна записати
у вигляді
![]() .
.
Матрицю (17) будемо називати елементарною трикутною матрицею, що відповідає першому кроку виключення методу Гаусса.
Перепишемо систему (16) у вигляді
![]() ,
,
![]() , (18)
, (18)
![]() .
.
Здійснимо
другий крок
методу Гаусса,
тобто виключимо
невідому
![]() з останнього
рівняння.
з останнього
рівняння.
Тоді одержимо систему вигляду
![]() ,
,
![]() , (19)
, (19)
![]() .
.
Можна переконатися,що перехід від (18) до (19) здійснюється завдяки множення системи (18) на елементарну трикутну матрицю
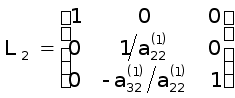 . (20)
. (20)
Таким чином,після другого кроку виключення приходимо до системи
![]() ,
(21)
,
(21)
де матриці
![]() і
і
![]() означені згідно
(17), (20).
означені згідно
(17), (20).
Нарешті, перемножаючи (21) на матрицю
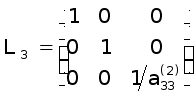
одержимо систему
![]() , (22)
, (22)
матриця
якої
![]() є верхньою
трикутною
матрицею з
одиничною
головною діагоналлю.
є верхньою
трикутною
матрицею з
одиничною
головною діагоналлю.
Звідки
виходить, зокрема,
що A=LU,
де
![]() -нижня
трикутна матриця.
-нижня
трикутна матриця.
Таким
чином,
![]() -розклад матриці
А
може бути одержаний
за допомогою
елементарних
трикутних
матриць: спочатку
будуються
матриці
-розклад матриці
А
може бути одержаний
за допомогою
елементарних
трикутних
матриць: спочатку
будуються
матриці
![]() та обчислюється
та обчислюється
![]() ,
а потім відшукується
,
а потім відшукується
![]() .Відзначимо,
що матриці
.Відзначимо,
що матриці
![]() мають простий
вигляд
мають простий
вигляд
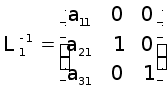 ;
;
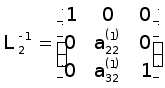 ;
;
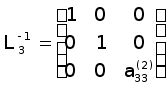 ;
;
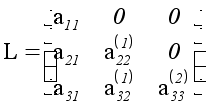 .
.
причому на діагоналі матриці містяться ведучі елементи методу виключення.
Запис методу Гаусса у вигляді (22) детально описує процес виключення.
Усе згадане раніш переноситься без винятку на системи рівнянь довільного порядку (2).
Процес виключення можна записати формулою
![]() , (23)
, (23)
де елементарна
нижня трикутна
матриця
![]() на к-му
кроці виключення
має вигляд
на к-му
кроці виключення
має вигляд
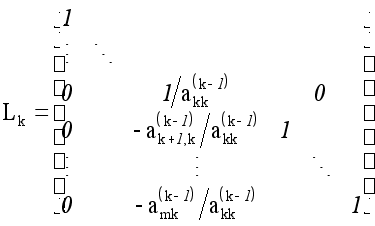 .
.
Матриця
![]() здійснює виключення
невідомого
здійснює виключення
невідомого
![]() з рівнянь з
номерами
к+1, к+2, ... ,m.
з рівнянь з
номерами
к+1, к+2, ... ,m.
Матриці
![]() існують і мають
вигляд
існують і мають
вигляд
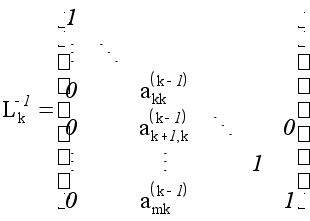 .
.
МЕТОД ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.
Основная идея метода. Может оказаться, что система
Ax=f (1)
имеет единственное решение, хотя какой-либо из угловых миноров матрицы А равен нулю. В этом случае обычный метод Гаусса оказывается непригодным, но может быть применен метод Гаусса с выбором главного элемента.
Основная
идея метода
состоит в том,
чтобы на очередном
шаге исключать
не следующее
по номеру
неизвестное,
а то
неизвестное,
коэффициент
при котором
является наибольшим
по модулю. Таким
образом, в качестве
ведущего элемента
здесь выбирается
главный,
т.е. наибольший
по модулю элемент.
Тем самым, если
![]() ,
то в процессе
вычислений
не будет происходить
деление на
нуль.
,
то в процессе
вычислений
не будет происходить
деление на
нуль.
Различные варианты метода Гаусса с выбором главного элемента проиллюстрируем на примере системы из двух уравнений
![]() (2)
(2)
![]()
![]()
![]()
![]() Предположим,
что
Предположим,
что
![]() .
Тогда на первом
шаге будем
исключать
переменное
.
Тогда на первом
шаге будем
исключать
переменное
![]() .
Такой прием
эквивалентен
тому, что система
(2) переписывается
в виде
.
Такой прием
эквивалентен
тому, что система
(2) переписывается
в виде
![]() (3)
(3)
![]()
и к (3) применяется первый шаг обычного метода Гаусса. Указанный способ исключения называется методом Гаусса с выбором главного элемента по строке. Он эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация переменных.
Применяется
также метод
Гаусса с выбором
главного элемента
по столбцу.
Предположим,
что
![]() .
Перепишем
систему (2) в
виде
.
Перепишем
систему (2) в
виде
![]()
![]()
и к новой системе применим на первом шаге обычный метод Гаусса. Таким образом, метод Гаусса с выбором главного элемента по столбцу эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация уравнений.
Иногда применяется и метод Гаусса с выбором главного элемента по всей матрице, когда в качестве ведущего выбирается максимальный по модулю элемент среди всех элементов матрицы системы.
Матрицы перестановок. Ранее было показано, что обычный метод Гаусса можно записать в виде
![]()
![]()
где
![]() -элементарные
нижние треугольные
матрицы. Чтобы
получить аналогичную
запись метода
Гаусса с выбором
главного элемента,
необходимо
рассмотреть
матрицы перестановок.
-элементарные
нижние треугольные
матрицы. Чтобы
получить аналогичную
запись метода
Гаусса с выбором
главного элемента,
необходимо
рассмотреть
матрицы перестановок.
ОПРЕДЕЛЕНИЕ 1. Матрицей перестановок Р называется квадратная матрица, у которой в каждой строке и в каждом столбце только один элемент отличен от нуля и равен единице.
ОПРЕДЕЛЕНИЕ
2.
Элементарной
матрицей перестановок
![]() называется
матрица, полученная
из единичной
матрицы перестановкой
называется
матрица, полученная
из единичной
матрицы перестановкой
![]() к-й
и l-й
строк.
к-й
и l-й
строк.
Например, элементарными матрицами перестановок третьего порядка являются матрицы
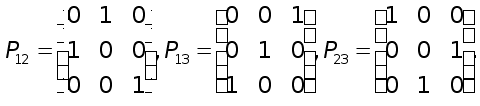
Можно отметить следующие свойства элементарных матриц перестановок, вытекающие непосредственно из их определения .
Произведение двух (а следовательно, и любого числа) элементарных матриц перестановок является матрицей перестановок (не обязательно элементарной).
Для любой квадратной матрицы А матрица
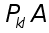 отличается
от А
перестановкой
к-й
и
l-й
строк.
отличается
от А
перестановкой
к-й
и
l-й
строк.Для любой квадратной матрицы А матрица
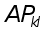 отличается
от А
перестановкой
к-го
и l-го
столбцов.
отличается
от А
перестановкой
к-го
и l-го
столбцов.
Применение элементарных матриц перестановок для описания метода Гаусса с выбором главного элемента по столбцу можно пояснить на следующем примере системы третьего порядка:
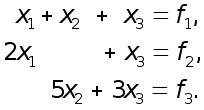 (4)
(4)
Система имеет вид (1), где
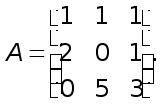 (5)
(5)
Максимальный элемент первого столбца матрицы А находится во второй строке. Поэтому надо поменять местами вторую и первую строки и перейти к эквивалентной системе
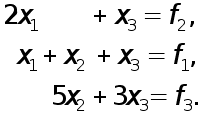 (6)
(6)
Систему (6) можно записать в виде
![]() (7)
(7)
т.е. она получается из системы (4) путем умножения на матрицу
перестановок
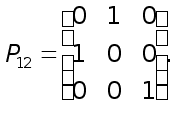
Далее, к системе (6) надо применить первый шаг обычного метода исключения Гаусса. Этот шаг эквивалентен умножению системы (7) на элементарную нижнюю треугольную матрицу
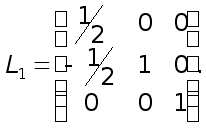
В результате от системы (7) перейдем к эквивалентной системе
![]() (8)
(8)
или в развернутом виде
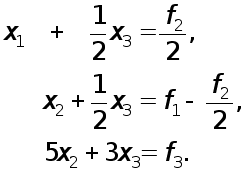 (9)
(9)
Из последних
двух уравнений
системы (9) надо
теперь исключить
переменное
![]() .
Поскольку
максимальным
элементом
первого столбца
укороченной
системы
.
Поскольку
максимальным
элементом
первого столбца
укороченной
системы
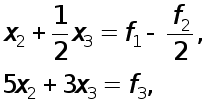 (10)
(10)
является элемент второй строки, делаем в (10) перестановку строк и тем самым от системы (9) переходим к эквивалентной системе
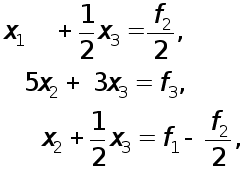 (11)
(11)
которую можно записать в матричном виде как
![]() .
(12)
.
(12)
Таким образом система (12) получена из (8) применением элемен-тарной матрицы перестановок
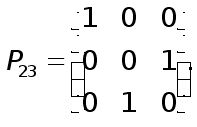
Далее к системе (11) надо применить второй шаг исключения обычного метода Гаусса. Это эквивалентно умножению системы (11) на элементарную нижнюю треугольную матрицу
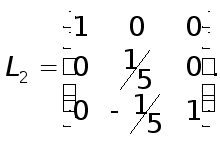
В результате получим систему
![]() (13)
(13)
или
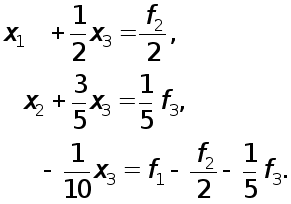 (14)
(14)
Заключительный шаг прямого хода метода Гаусса состоит в замене последнего уравнения системы (14) уравнением
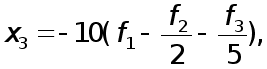
что эквивалентно умножению (13) на элементарную нижнюю треугольную матрицу
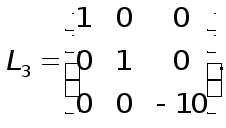
Таким образом, для рассмотренного примера процесс исключения Гаусса с выбором главного элемента по столбцу записывается в
виде
![]() (15)
(15)
По построению матрица
![]() (16)
(16)
является верхней треугольной матрицей с единичной главной диагональю.
Отличие
от обычного
метода Гаусса
состоит в том,
что в качестве
сомножителей
в (16) наряду с
элементарными
треугольными
матрицами
![]() могут
присутствовать
элементарные
матрицы перестановок
могут
присутствовать
элементарные
матрицы перестановок
![]() .
.
Покажем еще, что из (16) следует разложение
PA=LU, (17)
где L -нижняя треугольная матрица, имеющая обратную, P - матрица перестановок.
Для этого найдем матрицу
![]() (18)
(18)
По свойству
2) матрица
![]() получается
из матрицы
получается
из матрицы
![]() перестановкой
второй и третьей
строк,
перестановкой
второй и третьей
строк,
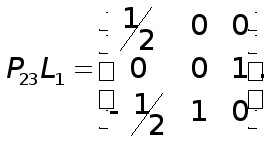
Матрица
![]() согласно
свойству 3)
получается
из
согласно
свойству 3)
получается
из
![]() перестановкой
второго и третьего
столбцов
перестановкой
второго и третьего
столбцов
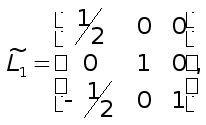
т.е.
![]() -нижняя
треугольная
матрица, имеющая
обратную.
-нижняя
треугольная
матрица, имеющая
обратную.
Из (18), учитывая
равенство
![]() ,
получим
,
получим
![]() (19)
(19)
Отсюда и из (16) видно, что
![]()
где обозначено
![]() .
Поскольку
Р-матрица
перестановок
и L-нижняя
треугольная
матрица, свойство
(17) доказано. Оно
означает, что
метод Гаусса
с выбором главного
элемента по
столбцу эквивалентен
обычному методу
Гаусса, примененному
к матрице РА,
т.е. к системе,
полученной
из исходной
системы перестановкой
некоторых
уравнений.
.
Поскольку
Р-матрица
перестановок
и L-нижняя
треугольная
матрица, свойство
(17) доказано. Оно
означает, что
метод Гаусса
с выбором главного
элемента по
столбцу эквивалентен
обычному методу
Гаусса, примененному
к матрице РА,
т.е. к системе,
полученной
из исходной
системы перестановкой
некоторых
уравнений.
Общий вывод. Результат, полученный ранее для очень частного примера, справедлив и в случае общей системы уравнений (1).
А именно, метод Гаусса с выбором главного элемента по столбцу можно записать в виде
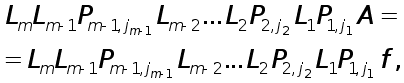 (20)
(20)
где
![]() -
элементарные
матрицы перестановок
такие, что
-
элементарные
матрицы перестановок
такие, что
![]() и
и
![]() -элементарные
нижние треугольные
матрицы.
-элементарные
нижние треугольные
матрицы.
Отсюда, используя соотношения перестановочности, аналогичные (19), можно показать, что метод Гаусса с выбором главного элемента эквивалентен обычному методу Гаусса, примененному к системе
PAx=Pf, (21)
где Р - некоторая матрица перестановок.
Теоретическое обоснование метода Гаусса с выбором главного элемента содержится в следующей теореме.
ТЕОРЕМА
1. Если
![]() то
существует
матрица перестано-
то
существует
матрица перестано-
вок Р такая, что матрица РА имеет отличные от нуля угловые ми-
норы.
Доказательство в п.4.
СЛЕДСТВИЕ.
Если
![]() то
существует
матрица престана-
то
существует
матрица престана-
вок Р такая, что справедливо разложение
РА=LU, (22)
где L- нижняя треугольная матрица с отличными от нуля диагональными элементами и U- верхняя треугольная матрица с единичной главной диагональю. В этом случае для решения системы (1) можно применять метод Гаусса с выбором главного элемента.
4. Доказательство теоремы 1. Докажем теорему индукцией по числу m -порядку матрицы А.
Пусть m=2, т.е.
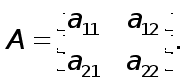
Если
![]() то утверждение
теоремы выполняется
при Р=Е,
где Е
- единичная
матрица второго
порядка. Если
то утверждение
теоремы выполняется
при Р=Е,
где Е
- единичная
матрица второго
порядка. Если
![]() ,
то
,
то
![]() ,
т.к.
,
т.к.
![]() При
этом у матрицы
При
этом у матрицы
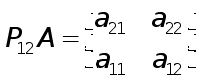
все угловые миноры отличны от нуля.
Пусть утверждение теоремы верно для любых квадратных матриц порядка m-1. Покажем, что оно верно и .для матриц порядка m. Разобьем матрицу А порядка m на блоки
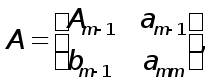
где
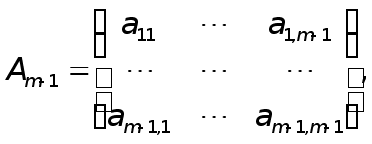
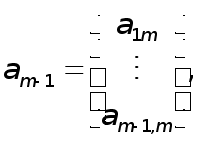
![]()
Достаточно
рассмотреть
два случая :![]() и
и
![]() .
В первом случае
по предположению
индукции существует
матрица перестановок
.
В первом случае
по предположению
индукции существует
матрица перестановок
![]() порядка
m-1
такая,
что
порядка
m-1
такая,
что
![]() имеет
отличные от
нуля угловые
миноры. Тогда
для матрицы
перестановок
имеет
отличные от
нуля угловые
миноры. Тогда
для матрицы
перестановок
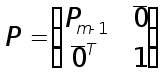
имеем
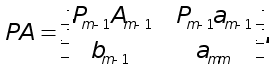
причем
![]() .
Тем самым все
угловые миноры
матрицы РА
отличны
от нуля.
.
Тем самым все
угловые миноры
матрицы РА
отличны
от нуля.
Рассмотрим
второй случай,
когда![]() . Т.к.
. Т.к.![]() , найдется хотя
бы один отличный
от нуля минор
порядка m-1
матрицы
А,
полученный
вычеркиванием
последнего
столбца и какой-либо
строки. Пусть,
например,
, найдется хотя
бы один отличный
от нуля минор
порядка m-1
матрицы
А,
полученный
вычеркиванием
последнего
столбца и какой-либо
строки. Пусть,
например,
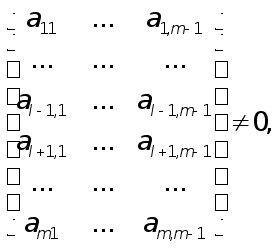
где
![]() .
.
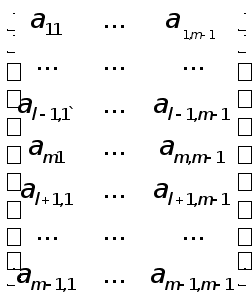
Переставляя
в матрице А
строки
с номерами l
и m,
получим
матрицу
![]() ,
у
которой угловой
минор порядка
m-1 имеет
вид
,
у
которой угловой
минор порядка
m-1 имеет
вид
и отличается от (23) только перестановкой строк. Следовательно, этот минор не равен нулю и мы приходим к рассмотренному выше случаю.
Теорема доказана.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МЕТОДОМ ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.
Одновременно с решением системы линейных алгебраических уравнений
![]()
можно вычислить определитель матрицы А.
Пусть в процессе исключения найдено распожение
![]()
т.е. построены матрицы L и U . Тогда
![]()
и, таким образом, произведение диагональных елементов матрицы L (ведущих, главных елементов метода исключения) равно определителю матрицы РА. Поскольку матрицы РА и А отличаются только перестановкой строк, определитель матрицы РА может отличаться от определителей матрицы А только знаком.
А
именно,
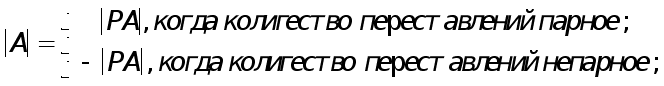
Таким образом, для вычисления определителя необходимо знать, сколько перестановок было осуществлено в процессе сключения.
Если матрица А выроджена, то при использовании метод Гаусса с выбором главного элемента по столбцу на некотором шаге исключения К все элементы которого столбца, находящиеся ниже главной диагонали и на ней, окажутся равными нулю.При этом дальнейшее исключение становится невозможным и программа должна выдать информацию о том, что определитель матрицы равен нулю.
ОБРАЩЕНИЕ МАТРИЦ.
Нахождение матрицы, обратной матрице А , еквивалентно решению матричного уравнения
![]() (1)
(1)
где Е - единичная матрица, X - искомая квадратная матрица.
Уравнение
(1) можно записать
в виде системы
![]() уравнений
уравнений
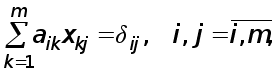 (2)
(2)
где
![]()
Можно заметить, что система (2) распадается на m независимых систем уравнений с одной и той же матрицей А , но с различными правыми частями. Эти системы имеют
вид ( фиксируем j ) :
![]() (3)
(3)
где
![]() у вектора - столбца
у вектора - столбца
![]() равна единице
j-та
компонента
и равны нулю
остальные
компоненты.
равна единице
j-та
компонента
и равны нулю
остальные
компоненты.
Например, для матрицы второго порядка система (2) распадается на две независимые системы:

Для решения систем (3) используется метод Гаусса ( обычный или с выбором главного элемента).
Рассмотрим применение метода Гаусса без выбора главного элемента. Поскольку все системы (3) имеют одну и ту же матрицу А , достаточно один раз совершить прямой ход метода Гаусса, т.е. получить разложение A=LU и запомнить матрицы L i U .
Обратный
ход осуществляется
путем решения
систем уравнений
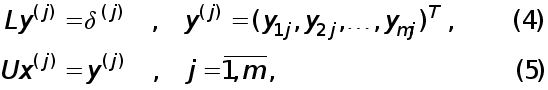
с треугольными матрицами L и U.
При осуществлении обратного хода можно сократить число действий, принимая во внимание специальный вид правых частей системы (4).
Запишем подробнее первые j-1 уравнений системы (4):
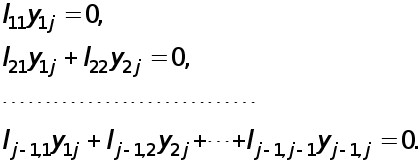
Учитывая
невырожденность
матрицы L
( т.е.
![]()
отсюда получаем
![]()
При
этом оставшиеся
уравнения
системы (4) имеют
вид
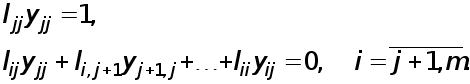
Отсюда
последовательно
находятся
неизвестные
![]() по формулам:
по формулам:
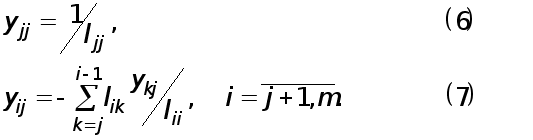
Можно
показать, что
общее число
действий умножения
и деления,
необходимое
для обращения
матрицы указанным
способом, порядка
![]() .
Тем самым обращение
матрицы требует
не намного
больше времени,
чем решение
системы уравнений.
.
Тем самым обращение
матрицы требует
не намного
больше времени,
чем решение
системы уравнений.
ІТЕРАЦІЙНІ МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ
АЛГЕБРАЇЧНИХ РІВНЯНЬ.
Розглядається система лінійних алгебраїчних рівнянь
![]() (1)
(1)
де
 - квадратна
матриця вимірності
- квадратна
матриця вимірності
![]()
![]()
![]() -
вектор - стовпець
правих частин
системи;
-
вектор - стовпець
правих частин
системи;
![]() - вектор - стовпець
невідомих.
- вектор - стовпець
невідомих.
Ідея найпростіших ітераційних методів розв’язання системи (1) полягає у наступному. За допомогою еквівалентних перетво-рень система (1) зводиться до системи вигляду
![]() (2)
(2)
де
![]() -квадратна
матріця
-квадратна
матріця
![]()
![]() -відомий
вектор.
-відомий
вектор.
А
потім задається
деяке початкове
наближення
![]() (наприклад,
у якості
(наприклад,
у якості
![]() береться вектор
береться вектор
![]() , або деякий
розв’язок
системи (1), який
одержується
іншим методом
з деякою похибкою).
Інші наближення
послі-довно
знаходяться
за рекурентною
формулою
, або деякий
розв’язок
системи (1), який
одержується
іншим методом
з деякою похибкою).
Інші наближення
послі-довно
знаходяться
за рекурентною
формулою
![]() (3)
(3)
доки
на деякому
кроці не буде
досягнута
задана точність
![]()
обчислення
значення невідомого
вектору
![]() .
.
Виникає
питання, за
яких умов на
![]() послідовність
послідовність![]()
збігається
(у певному розумінні)
до точного
розв’язку
![]() .
.
Не
зупиняючись
на подробицях
(дивись спецкурс
‘Додат-кові
розділи чисельного
аналізу’),
дамо деякі
достатні умови,
за яких
![]()
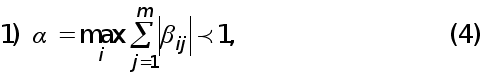
або
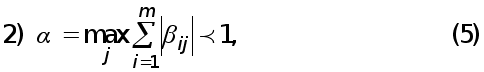
або
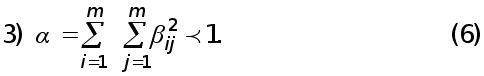
Швидкість збіжності оцінюється нерівністю
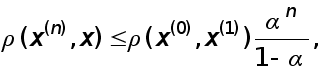
де
![]() -
відстань між
векторами
-
відстань між
векторами
![]() та
та
![]() ,
що може бути
заданою:
,
що може бути
заданою:
![]() коли
виконується
умова (4);
коли
виконується
умова (4);
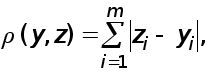 коли виконується
умова (5);
коли виконується
умова (5);
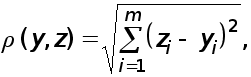 коли
виконується
умова (6).
коли
виконується
умова (6).
Задаючи
потрібну точність
![]() можна з рівності
можна з рівності
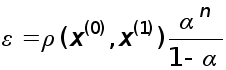
одержати
необхідну
кількість
ітерацій
![]() ,
щоб досягти
задане
,
щоб досягти
задане
![]() .
.
Наведені умови є достатніми для збіжності методу ітерацій, але аж ніяк не необхідними. Необхідні і достатні умови збіжності методу ітерацій дає наступна теорема, яку сформулюємо без доведення.
ТЕОРЕМА:
Нехай система
(2) має єдиний
розв’язок.
Послідовні
наближення
(3) збігаються
до розв’язку
системи (2) за
довільного
початкового
наближення
![]() тоді та й тільки
тоді, коли усі
власні значення
матриці
тоді та й тільки
тоді, коли усі
власні значення
матриці
![]() за модулем
менше одиниці.
за модулем
менше одиниці.
Повернемось зараз до способів приведення (1) до форми (2). Запишемо (1) у розгорнутій формі
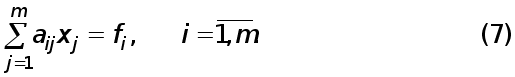 Якщо
Якщо
![]() для усіх
для усіх
![]() , то можна (7)
зобразити у
вигляді
, то можна (7)
зобразити у
вигляді
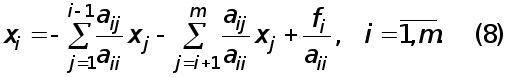
Звідси два найпростіших ітераційних метода.
Метод Якобі, який задається рекурентним співвідношенням:
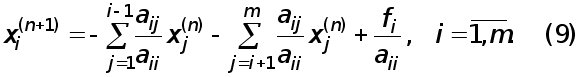
Метод Зейделя, де вже знайдені компоненти беруться у правій частині співвідношення з (n+1)-го наближення, а інші- з n-го наближення:
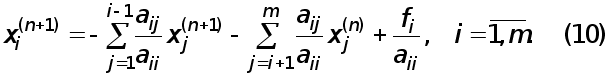
Можна дати матричну форму методів Якобі і Зейделя.
Нехай матрицю А наведено у вигляді:
![]()
де
![]() -нижня трикутна
матриця з нульовою
головною діагонал-лю;
-нижня трикутна
матриця з нульовою
головною діагонал-лю;
D
- діагональна
матриця з
![]() на головній
діагоналі;
на головній
діагоналі;
![]() -верхня
трикутна матриця
з нульовою
головною діагоналлю.
-верхня
трикутна матриця
з нульовою
головною діагоналлю.
За
припущенням
![]() існує
існує
![]()
Тоді зображенню у формі (8) відповідає
![]()
або
![]()
Таким чином, методу Якобі відповідає ітераційна процедура
![]()
Методу Зейделя відповідає
![]()
Використовуючи
сформульовані
раніш достатні
умови збіжності
![]() , самостійно
переконайтесь,
що достатніми
умовами збіжності
методу Якобі
є
, самостійно
переконайтесь,
що достатніми
умовами збіжності
методу Якобі
є
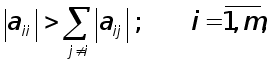
або
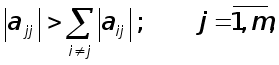
тобто діагональне переваження матриці А.
Можна довести, що за вказаних умов збігається і метод Зейделя.
Покажемо,
що до форми
(2), що задовольняє
умовам збіжності,
може бути зведена
довільна система
(1) з
![]()
Дійсно,візьмемо
матрицю
![]() де
де
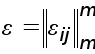 -матриця
з достатньо
малими за модулем
елементами.
Множачи (1) зліва
на С маємо
-матриця
з достатньо
малими за модулем
елементами.
Множачи (1) зліва
на С маємо
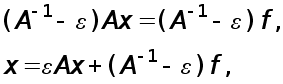
тобто
одержали форму
(2) з
![]()
За
рахунок вибору
достатньо малих
![]() можна задовольнити
умовам збіжності.
можна задовольнити
умовам збіжності.
Процес ітерації, що збігається, володіє властивістю стій-кості, тобто окрема похибка у обчисленнях не позначається на кінцевому результаті, тому що хибне наближення можна роз-глядати як новий початковий вектор.
ІТЕРАЦІЙНІ МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ
АЛГЕБРАЇЧНИХ РІВНЯНЬ.
Розглядається система лінійних алгебраїчних рівнянь
![]() (1)
(1)
де
 - квадратна
матриця вимірності
- квадратна
матриця вимірності
![]()
![]()
![]() -
вектор - стовпець
правих частин
системи;
-
вектор - стовпець
правих частин
системи;
![]() -
вектор - стовпець
невідомих.
-
вектор - стовпець
невідомих.
Ідея найпростіших ітераційних методів розв’язання системи (1) полягає у наступному. За допомогою еквівалентних перетворень система (1) зводиться до системи вигляду
![]() (2)
(2)
де
![]() -квадратна
матріця
-квадратна
матріця
![]()
![]() -відомий
вектор.
-відомий
вектор.
А
потім задається
деяке початкове
наближення
![]() (наприклад,
у якості
(наприклад,
у якості
![]() береться вектор
береться вектор
![]() , або деякий
розв’язок
системи (1), який
одержується
іншим методом
з деякою похибкою).
Інші наближення
послідовно
знаходяться
за рекурентною
формулою
, або деякий
розв’язок
системи (1), який
одержується
іншим методом
з деякою похибкою).
Інші наближення
послідовно
знаходяться
за рекурентною
формулою
![]() (3)
(3)
доки
на деякому
кроці не буде
досягнута
задана точність
![]()
обчислення
значення невідомого
вектору
![]() .
.
Виникає
питання, за
яких умов на
![]() послідовність
послідовність![]()
збігається
(у певному розумінні)
до точного
розв’язку
![]() .
.
Не
зупиняючись
на подробицях
(дивись спецкурс
‘Додаткові
розділи чисельного
аналізу’),
дамо деякі
достатні умови,
за яких
![]()
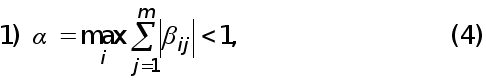
або
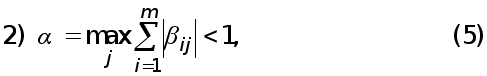
або
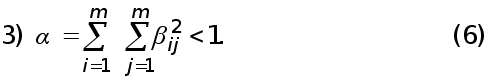
Швидкість збіжності оцінюється нерівністю
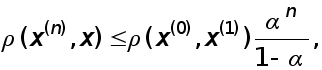
де
![]() -
відстань між
векторами
-
відстань між
векторами
![]() та
та
![]() ,
що може бути
заданою:
,
що може бути
заданою:
![]() коли
виконується
умова (4);
коли
виконується
умова (4);
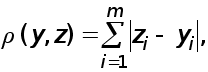 коли
виконується
умова (5);
коли
виконується
умова (5);
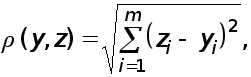 коли
виконується
умова (6).
коли
виконується
умова (6).
Задаючи
потрібну точність
![]() можна з рівності
можна з рівності
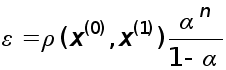
одержати
необхідну
кількість
ітерацій
![]() ,
щоб досягти
задане
,
щоб досягти
задане
![]() .
.
Наведені умови є достатніми для збіжності методу ітерацій, але аж ніяк не необхідними. Необхідні і достатні умови збіжності методу ітерацій дає наступна теорема, яку сформулюємо без доведення.
ТЕОРЕМА:
Нехай система
(2) має єдиний
розв’язок.
Послідовні
наближення
(3) збігаються
до розв’язку
системи (2) за
довільного
початкового
наближення
![]() тоді та й тільки
тоді, коли усі
власні значення
матриці
тоді та й тільки
тоді, коли усі
власні значення
матриці
![]() за модулем
менше одиниці.
за модулем
менше одиниці.
Повернемось зараз до способів приведення (1) до форми (2). Запишемо (1) у розгорнутій формі
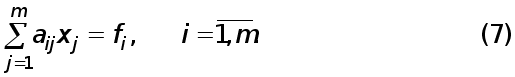 Якщо
Якщо
![]() для усіх
для усіх
![]() ,
то можна (7) зобразити
у вигляді
,
то можна (7) зобразити
у вигляді
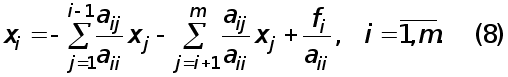
Звідси два найпростіших ітераційних метода.
Метод Якобі, який задається рекурентним співвідношенням:
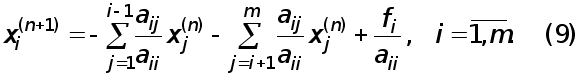
Метод Зейделя, де вже знайдені компоненти беруться у правій частині співвідношення з (n+1)-го наближення, а інші- з n-го наближення:
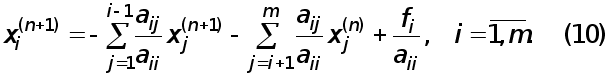
Можна дати матричну форму методів Якобі і Зейделя.
Нехай матрицю А наведено у вигляді:
![]()
де
![]() -нижня
трикутна матриця
з нульовою
головною діагоналлю;
-нижня
трикутна матриця
з нульовою
головною діагоналлю;
D
- діагональна
матриця з
![]() на головній
діагоналі;
на головній
діагоналі;
![]() -верхня
трикутна матриця
з нульовою
головною діагоналлю.
-верхня
трикутна матриця
з нульовою
головною діагоналлю.
За
припущенням
![]() існує
існує
![]()
Тоді зображенню у формі (8) відповідає
![]()
або
![]()
Таким чином, методу Якобі відповідає ітераційна процедура
![]()
Методу Зейделя відповідає
![]()
Використовуючи
сформульовані
раніш достатні
умови збіжності
![]() ,
самостійно
переконайтесь,
що достатніми
умовами збіжності
методу Якобі
є
,
самостійно
переконайтесь,
що достатніми
умовами збіжності
методу Якобі
є
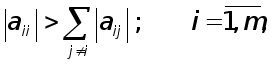
або
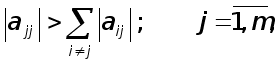
тобто діагональне переваження матриці А.
Можна довести, що за вказаних умов збігається і метод Зейделя.
Покажемо,
що до форми
(2), що задовольняє
умовам збіжності,
може бути зведена
довільна система
(1) з
![]()
Дійсно,візьмемо
матрицю
![]() де
де
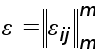 -матриця
з достатньо
малими за модулем
елементами.
Множачи (1) зліва
на С
маємо
-матриця
з достатньо
малими за модулем
елементами.
Множачи (1) зліва
на С
маємо
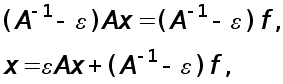
тобто
одержали форму
(2) з
![]()
За
рахунок вибору
достатньо малих
![]() можна задовольнити
умовам збіжності.
можна задовольнити
умовам збіжності.
Процес ітерації, що збігається, володіє властивістю стійкості, тобто окрема похибка у обчисленнях не позначається на кінцевому результаті, тому що хибне наближення можна розглядати як новий початковий вектор.
МЕТОД ПРОГОНКИ.
Система уравнений для определения коэффициентов сплайна представляет собой частный случай систем линейных алгебраических уравнений
![]()
с
трехдиагональной
матрицей
![]() ,
т.е. с матрицей,
все элементы
которой,не
лежащие на
главной и двух
побочных диагоналях,
равны нулю
,
т.е. с матрицей,
все элементы
которой,не
лежащие на
главной и двух
побочных диагоналях,
равны нулю
![]() при
при
![]() та
та
![]()
В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид
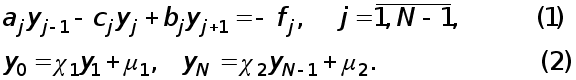
Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных.
Т.е. матрицу А можно записать
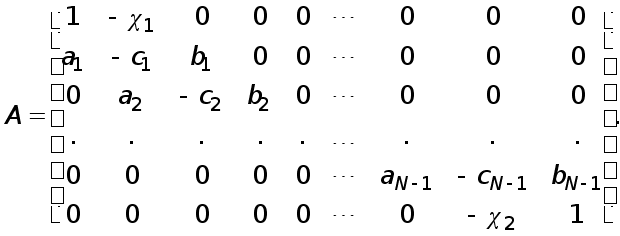
Идея метода прогонки состоит в следующем. Решение системы (1) ищется в виде
![]()
где
![]() -неизвестные
коэффициенты,
которые последовательно
находятся от
-неизвестные
коэффициенты,
которые последовательно
находятся от
![]() до
до
![]() (прямая прогонка
),
а затем последовательно
вычисляются
(прямая прогонка
),
а затем последовательно
вычисляются
![]() (обратная прогонка)
.
(обратная прогонка)
.
Выведем
формулы для
вычисления
![]() Из (3) можно получить
Из (3) можно получить
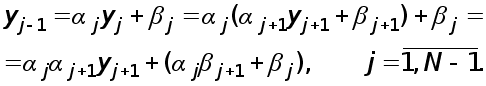
Подставляя
имеющиеся
выражения для
![]() в уравнение
(1),приходим при
в уравнение
(1),приходим при
![]() к уравнению
к уравнению
![]() Последнее
уравнение будет
выполнено если
коэффициенты
Последнее
уравнение будет
выполнено если
коэффициенты
![]() выбрать такими,
чтобы выражения
в квадратных
скобках обращались
в нуль.
выбрать такими,
чтобы выражения
в квадратных
скобках обращались
в нуль.
А именно,
достаточно
положить
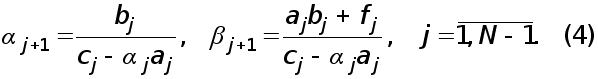 Для
отыскания всех
Для
отыскания всех
![]() достаточно
задать
достаточно
задать
![]()
Эти
начальные
значения находим
из требования
эквивалентности
условия (3) при
![]() т.е. условия
т.е. условия
![]() , первому из
уравнений (2).
, первому из
уравнений (2).
Таким образом, получаем
![]() (5)
(5)
Нахождение
коэффициентов
![]() по формулам
(4), (5) называется
прямой
прогонкой.
После того,
как прогоночные
коэффициенты
по формулам
(4), (5) называется
прямой
прогонкой.
После того,
как прогоночные
коэффициенты
![]() найдены,
решение системи
(1), (2) находится
по рекуррентной
формуле (3), начиная
с
найдены,
решение системи
(1), (2) находится
по рекуррентной
формуле (3), начиная
с
![]() Для начала
счета по этой
формуле требуется
знать
Для начала
счета по этой
формуле требуется
знать
![]() , которое определяется
из уравнений
, которое определяется
из уравнений
![]()
И равно
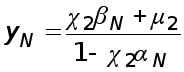 .
.
Нахождение
![]() по формулам
по формулам
 (6)
(6)
называется обратной прогонкой. Алгоритм решения системы (1), (2) определяемый формулами (4)-(6) называется методом прогонки.
Метод прогонки можно пременять, если знаменатели выражений (4), (6) не обрщаются в нуль.
Покажем, что для возможности применения метод прогонки достаточно потребовать, чтобы коэффициенты системы (1), (2) удовлетворяли условиям
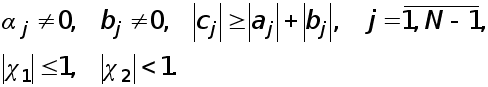 (8)
(8)
Сначала
докажем по
индукции, что
при условиях
(7), (8) модули прогоночных
коэффициентов
![]() не превосходят
единицы. Согласно
(5), (8) имеем
не превосходят
единицы. Согласно
(5), (8) имеем
![]() .
Предположим,что
.
Предположим,что
![]() для некоторого
для некоторого![]() и докажем, что
и докажем, что
![]()
Прежде
всего для любых
двух комплексных
чисел
![]() и
и
![]() докажем неравенство
докажем неравенство
![]()
Из неравенства треугольника имеем
![]()
Откуда
![]()
Вернемся
теперь к доказательству
![]() ,
если
,
если
![]() .
Согласно имеем
оценку
.
Согласно имеем
оценку
![]()
а, используя (7) , получаем
![]()
![]()
![]()
т.е. знаменатели выражений (4) не обращаются в нуль.
Более того
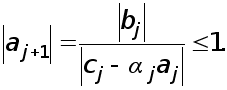
Следовательно,
![]()
Далее,
учитывая второе
из условий (8)
и только что
доказанное
неравенство
![]() ,
имеем
,
имеем
![]()
т.е.
не обращается
в нуль и знаменатель
в выражении
для
![]() .
.
К аналогичному выводу можно прийти и в том случае, когда условия (7), (8) заменяются условиями
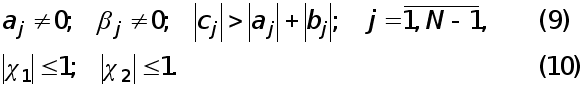 Таким
образом при
выполнении
условий (7), (8) (так
же как и условий
(9), (10)) система (1), (2)
эквивалентна
системе (4)-(6). Поэтому
эти условия
гарантируют
существование
и единственность
решения системы
(1), (2) и возможность
нахождения
этого решения
методом прогонки.
Таким
образом при
выполнении
условий (7), (8) (так
же как и условий
(9), (10)) система (1), (2)
эквивалентна
системе (4)-(6). Поэтому
эти условия
гарантируют
существование
и единственность
решения системы
(1), (2) и возможность
нахождения
этого решения
методом прогонки.
Кроме
того, доказанные
неравенства
![]() ,
,
![]() обеспечивают
устойчивость
счета по рекуррентным
формулам (6).
Последнее
означает, что
погрешность,внесенная
на каком-либо
шаге вычислений,
не будет возрастать
при переходе
к следующим
шагам.
обеспечивают
устойчивость
счета по рекуррентным
формулам (6).
Последнее
означает, что
погрешность,внесенная
на каком-либо
шаге вычислений,
не будет возрастать
при переходе
к следующим
шагам.
Действительно,
пусть в формуле
(6) при
![]() вместо
вместо
![]() вычислена
величина
вычислена
величина
![]()
Тогда
на следующем
шаге вычислений,
т.е. при
![]()
вместо
![]() получим
величину
получим
величину
![]() и погрешность
окажется равной
и погрешность
окажется равной
![]()
Отсюда
получаем, что
![]() ,т.е.
погрешность
не возрастает.
,т.е.
погрешность
не возрастает.
Подсчитаем число арифметических действий, выполняемых при решении задачи (1), (2) методом прогонки.
По формулам
(4), что реализуемые
с помощью шести
арифметических
действий, вычисления
производятся
![]() раз,
по формуле (6)
выполняется
5 арифметических
действий, наконец
по формуле
(3), требующей
всего два действия,
вычисления
осуществляются
раз,
по формуле (6)
выполняется
5 арифметических
действий, наконец
по формуле
(3), требующей
всего два действия,
вычисления
осуществляются
![]() раз.
Итак в методе
прогонки всего
затрачивается
раз.
Итак в методе
прогонки всего
затрачивается
![]()
арифметических
действий, т.е.
число действий
растет линейно
относительно
числа неизвестных
![]()
При решении же произвольной системы линейных алгебраических уравнений методом Гаусcа число действий пропорционально кубу числа неизвестных.
ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ.
Большое
число задач
математики
и физики требует
отыскания
собственных
значений и
собственных
векторов матриц,
т.е. отыскания
таких значений
+![]() ,
для которых
существуют
нетривиальные
решения однородной
системы линейных
алгебраических
уравнений
,
для которых
существуют
нетривиальные
решения однородной
системы линейных
алгебраических
уравнений
![]() , (1)
, (1)
и отыскания этих нетривиальных решений.
Здесь
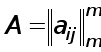 -квадратная
матрица порядка
m
,
-квадратная
матрица порядка
m
,
![]() -
неизвестный
вектор - столбец.
-
неизвестный
вектор - столбец.
Из курса алгебры известно, что нетривиальное решение системы (1) существует тогда и только тогда, когда
![]() ,
(2)
,
(2)
где Е
- единичная
матрица. Если
раскрыть определитель
![]() , получается
алгебраическое
уравнение
степени m
относительно
, получается
алгебраическое
уравнение
степени m
относительно
![]() .Таким
образом задача
отыскания
собственных
значений сводится
к проблеме
раскрытия
определителя
.Таким
образом задача
отыскания
собственных
значений сводится
к проблеме
раскрытия
определителя
![]() по степеням
по степеням
![]() и последующему
решению алгебраического
уравнения m-
й степени.
и последующему
решению алгебраического
уравнения m-
й степени.
Определитель
![]() называется
характеристическим
(или
вековым
) определителем,
а уравнение
(2) называется
характеристическим
(или
вековым
) уравнением.
называется
характеристическим
(или
вековым
) определителем,
а уравнение
(2) называется
характеристическим
(или
вековым
) уравнением.
Различают полную проблему собственных значений, когда необходимо отыскать все собственные значения матрицы А и соответствующие собственные векторы, и частичную проблему собственных значений, когда необходимо отыскать только некоторые собственные значения, например, максимальное по модулю собственное значение .
Метод Данилевского развертывание векового определителя.
Определение. Квадратная матрица Р порядка m называется подобной матрице А , если она представлена в виде
![]() ,
,
где S - невыродженная квадратная матрица порядка m.
ТЕОРЕМА. Характеристический определитель исходной и подобной матрицы совпадают .
Доказательство.
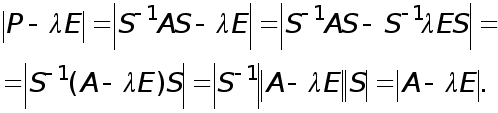
Идея метода Данилевского состоит в том, что матрица А подобным преобразованиям приводится, к так называемой нормальной форме Фробениуса
 .
.
Характеристическое уравнение для матрицы Р имеет простой вид
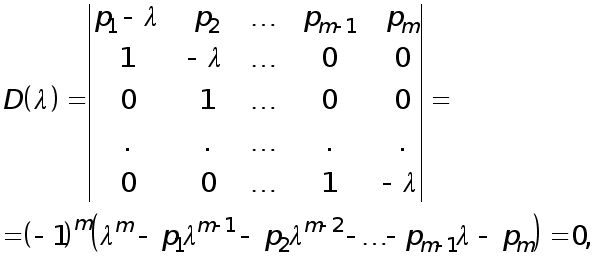 т.е.
коэффициенты
при степенях
т.е.
коэффициенты
при степенях
![]() характеристического
полинома
непосредственно
выражаются
через элементы
первой строки
матрицы Р.
характеристического
полинома
непосредственно
выражаются
через элементы
первой строки
матрицы Р.
Приведение матрицы А к нормальной форме Фробениуса Р осуществляется последовательно построкам, начиная с последеней строки.
Приведем матрицу А
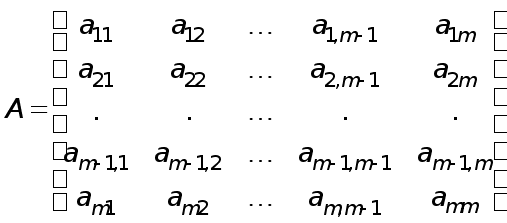
подобным преобразование к виду
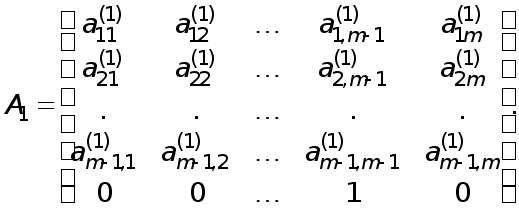
Пусть
![]() Можн проверить,что
такой вид имеет
матрица
Можн проверить,что
такой вид имеет
матрица
![]() ,
которая равна
,
которая равна
![]()
где
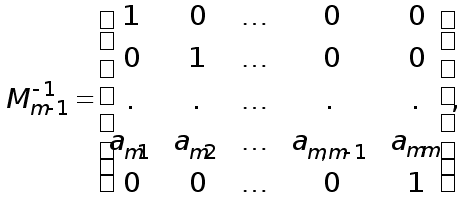
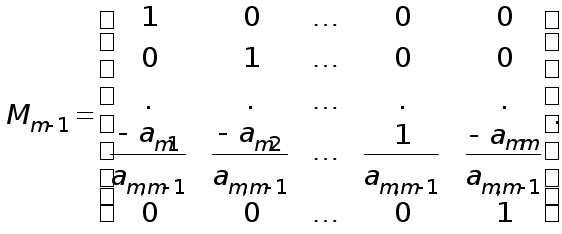
Слудующий
шаг - приведение
матрицы
![]() подобным
преобразованием
к виду
подобным
преобразованием
к виду
![]() ,
где и вторая
снизу строка
имеет единицу
в
,
где и вторая
снизу строка
имеет единицу
в
![]() -ом
столбце, а все
остальные
элементы строки
равны нулю:
-ом
столбце, а все
остальные
элементы строки
равны нулю:
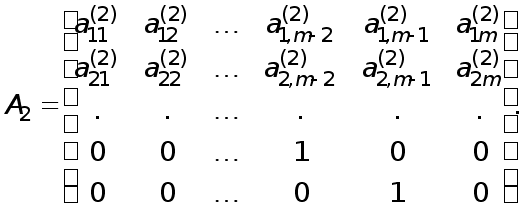
Если
![]() то
можно проверить,
что такой вид
имеет матрица
то
можно проверить,
что такой вид
имеет матрица
![]() :
:
![]()
где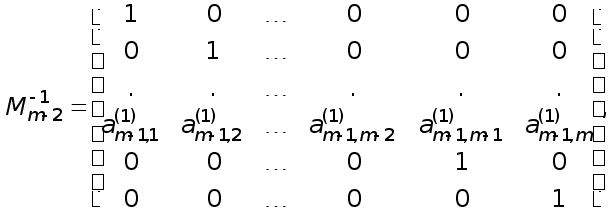
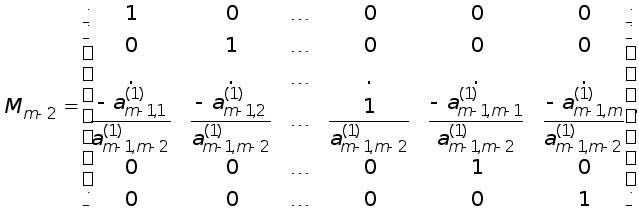
Таким образом
![]()
Далее процедура аналогичная, если на кождом шаге в очередной строке, на месте которого подобным преобразованием нужно получить единицу, не равную нулю.
В этом случае ( будем называт его регулярным ) нормальная формула Фробениуса будет получена за ( m-1 ) шагов и будет иметь вид
![]()
Рассмотрим нерегулярный случай, когда матрица, полученная в результате подобных преобразований приведена уже к виду
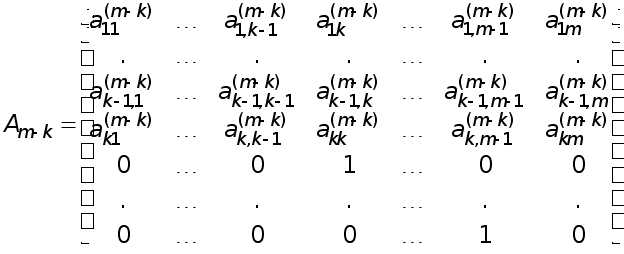 и
элемент
и
элемент
![]() . Таким образом
обычная процедура
метода Данилевского
не подходит
из-за необходимости
деления на
ноль.
. Таким образом
обычная процедура
метода Данилевского
не подходит
из-за необходимости
деления на
ноль.
В этой ситуации возможно два случая. В первом случае к-й
строке
левее элемента
![]() есть элемент
есть элемент
![]()
![]() Тогда
домножая матрицу
Тогда
домножая матрицу
![]() слева и справа
на
элементарную
матрицу перестановок
слева и справа
на
элементарную
матрицу перестановок
![]() ,
получаем матрицу
,
получаем матрицу
![]() ,
,
у которой
по сравнению
с матрицей
![]() переставлены
l
-я
и (k-1
)-я строка
l-й
и ( k-1)-
й стодбец.
В результате
на необходимом
нам месте оказывается
ненулевой
элемент
переставлены
l
-я
и (k-1
)-я строка
l-й
и ( k-1)-
й стодбец.
В результате
на необходимом
нам месте оказывается
ненулевой
элемент
![]() , уже преобразованная
часть матрицы
не меняется,
можно применять
обычный шаг
метода Данилевского
к матрице
, уже преобразованная
часть матрицы
не меняется,
можно применять
обычный шаг
метода Данилевского
к матрице
![]() .
Она подбна
матрице
.
Она подбна
матрице
![]() (и, следовательно,
исходной матрице
А ),
т.к. елементарная
матрица перестановок
совпадает со
своей обратной,
т.е.
(и, следовательно,
исходной матрице
А ),
т.к. елементарная
матрица перестановок
совпадает со
своей обратной,
т.е.
![]()
Рассмотрим
второй нерегулярный
случай, когда
в матрице
![]() элемент
элемент
![]() и все элементы
этой строки,
которые тоже
находятся левее
его, тоже равны
нулю. В этом
случае характеристический
определитель
матрицы
и все элементы
этой строки,
которые тоже
находятся левее
его, тоже равны
нулю. В этом
случае характеристический
определитель
матрицы
![]() можно представить
в виде
можно представить
в виде
![]()
где
![]() і
і
![]() - единичные
матрицы соответствующей
размерности,
а квадратные
матрицы
- единичные
матрицы соответствующей
размерности,
а квадратные
матрицы
![]() и
и
![]() имееют вид:
имееют вид:
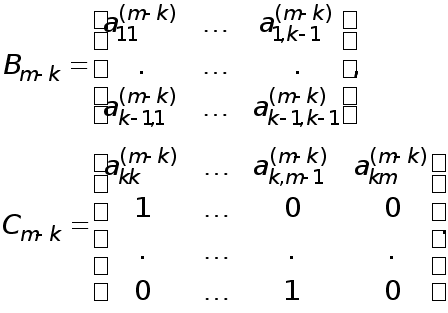
Обративм
внимание на
то, что матрица
![]() уже нормальную
форму Фробениуса,
и поэтому сомножитель
уже нормальную
форму Фробениуса,
и поэтому сомножитель
![]() просто развертывается
в виде многочлена
с коэффциентами,
равными элементам
первой строки.
просто развертывается
в виде многочлена
с коэффциентами,
равными элементам
первой строки.
Сомножитель
![]() ,
есть
характеристический
определитель
матрицы
,
есть
характеристический
определитель
матрицы
![]() .
Для развертывания
можн опять
применять метод
Данилевского,
приводя матрицу
.
Для развертывания
можн опять
применять метод
Данилевского,
приводя матрицу
![]() подобными
преобразованиями
к нормальной
форме Фробениуса.
подобными
преобразованиями
к нормальной
форме Фробениуса.
Предположим теперь, что матрица А подобным преобразованиям
![]() уже приведена
к нормальной
форме Фробениуса.
Решая характеристическое
уравнение
уже приведена
к нормальной
форме Фробениуса.
Решая характеристическое
уравнение
![]() ,
,
находим
одним из известных
методов его
корни
![]() которые являются
собственными
значениями
матрицы Р
и исходной
матрицы А.
которые являются
собственными
значениями
матрицы Р
и исходной
матрицы А.
Теперь
стоит задача
отыскать собственные
векторы, соответствующие
этим собственным
значениям, т.е.
векторы
![]() такие, что
такие, что
![]()
Решим ее следующим образом: найдем собственные векторы матрицы Р , а затем по определенному соотношению я пересчитаем собственные векторы матрицы А . Это соотношение дает следующая теорема.
ТЕОРЕМА.
Пусть
![]() є
есть собственное
значение , а
є
есть собственное
значение , а
![]() есть соответствующий
собственный
вектор матрицы
Р ,
которая подобна
матрице А
,т.е.
есть соответствующий
собственный
вектор матрицы
Р ,
которая подобна
матрице А
,т.е.
![]()
Тогда
![]() есть собственный
вектор матрицы
А
, соответствующий
собственному
значению
есть собственный
вектор матрицы
А
, соответствующий
собственному
значению
![]()
Доказательство.Тривиально следует из того, что
![]()
Домножая левую и правую часть этого равенства слева на S ,
имеем
![]()
А это и
означает, что
![]() -собственный
вектор матрицы
А ,
-собственный
вектор матрицы
А ,
отвечающий
собственному
значению
![]()
Найдем
собственный
вектор
матрицы Р
, которая
имеет нормальную
форму Фробениуса
и подобна матрице
А.
Записывая
![]() в развернутой
форме, имеем
в развернутой
форме, имеем
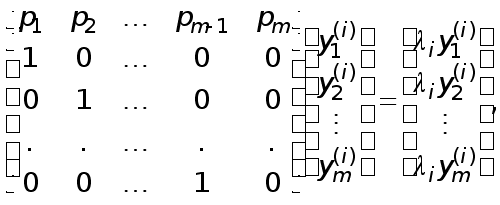
или
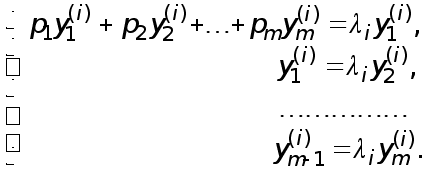
В этой
системе одна
из переменных
может быть
сделана свободной
и ей может быть
придано произвольное
значение. В
качестве таковой
возьмем
![]() и положим
и положим
![]()
Тогда последовательно находим
![]() ,
,
т.е. искомый собственный вектор матрицы Р имеет вид
 .
.
Если процесс приведения матрицы А к форме Р был регулярным, то
![]()
В соответствии
с теоремой
собственным
вектором матрицы
А
для собственного
значения
![]() будет вектор
будет вектор
![]()
Таким образом, задача вычисления собственных векторов матрицы А решена.
НАБЛИЖЕННЯ ФУНКЦІЙ. ЗАДАЧА ІНТЕРПОЛЯЦІЇ.
Задача наближення функцій виникає при розв’язанні багатьох задач ( обробка експериментальних даних, чисельне диференціювання та інтегрування функцій, розв’язання диференціальних та інтегральних рівнянь).
Дуже зручною у використанні на практиці функцією є многочлен. Щоб задати многочлен, треба задати тільки скінченну кількість його коефіцієнтів. Значення многочлена просто обчислюються (згадаємо схему Горнера), його легко продиференціювати, проінтегрувати і т.і. Тому алгебраїчні многочлени знайшли широке застосування для наближення (апроксимації) функцій.
Розглянемо декілька задач наближення функцій.
Постановка
задачі інтерполяції.
Нехай відомі
значення деякої
функції
![]() у
у
![]() різних
точках
різних
точках
![]() які позначимо
які позначимо
![]()
Виникає
задача поновлення
( наближеного)
функції
![]() у
довільній точці
у
довільній точці
![]() .
.
Іноді відомо, що наближену функцію доцільно шукати у вигляді
![]()
де
вигляд функції
![]() відомий,
а параметри
відомий,
а параметри
![]() треба
визначити.
треба
визначити.
Коли
параметри
![]() визначаються
з умови збігу
визначаються
з умови збігу![]() і наближеної
функції
і наближеної
функції
![]() у точках
у точках
![]() тобто
тобто
![]() то такий спосіб
наближення
називається
інтерполяцією.
Точки
то такий спосіб
наближення
називається
інтерполяцією.
Точки
![]() називаються
вузлами
інтерполяції.
називаються
вузлами
інтерполяції.
Серед способів інтерполяції найбільш поширеним є випадок лінійної інтерполяції .
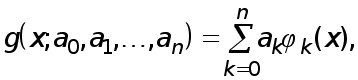
де
![]() - деякі відомі
функції. Значення
коефіцієнтів
- деякі відомі
функції. Значення
коефіцієнтів
![]() визначаються
з умови збігу
з вихідною
функцією у
вузлах інтерполяції
визначаються
з умови збігу
з вихідною
функцією у
вузлах інтерполяції
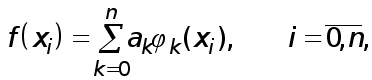 (1)
(1)
тобто
з системи n
+1
лінійних
рівнянь з n+1
невідомими
![]()
У
окремому випадку,
коли
![]()
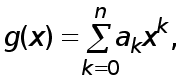 (2)
(2)
тобто інтерполяція здійснюється многочленом, який називається інтерполяційним.
ТЕОРЕМА. Якщо вузли интерполяції різні, то існує єдиний інтерполяційний многочлен n-го ступеню.
Доведення . Дійсно, система рівнянь (1) у цьому випадку має вигляд
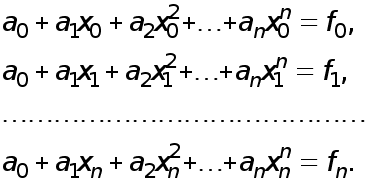 (3)
(3)
Її визначник є визначником Вандермонда
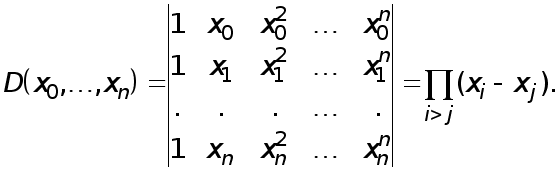 (4)
(4)
У тому, що має місце права частина рівності (4) , можна переконатися наступним чином.
Віднімаючи перший рядок з усіх наступних, маємо
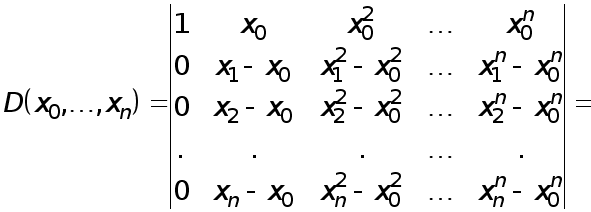
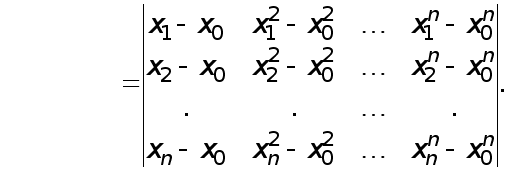
Віднімаючи
тепер з кожного
стовпця попередній,
що множиться
на
![]() одержуємо
одержуємо
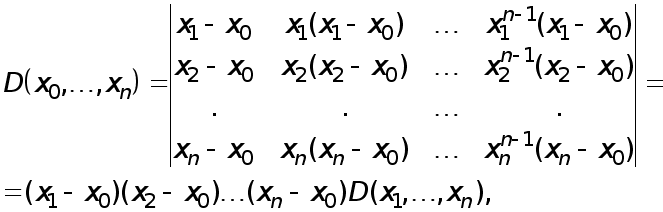 де
де
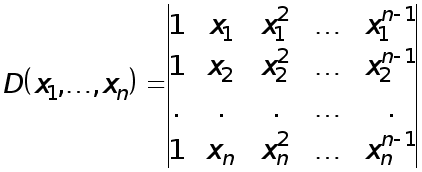
теж є визначником Вандермонда, порядок якого на одиницю менше порядку попереднього.
Зробивши з ним те ж, що з попереднім, одержимо
![]() Продовжуючи
аналогічні
викладки остаточно
одержимо рівність
(4).
Продовжуючи
аналогічні
викладки остаточно
одержимо рівність
(4).
Бачимо,
що при
![]() Тобто система
(3) має єдиний
розв’язок.
Теорема доведена.
Тобто система
(3) має єдиний
розв’язок.
Теорема доведена.
Таким чином, інтерполяційний поліном можна одержати шляхом розв’язання системи лінійних алгебраїчних рівнянь (3).
Інтерполяційний многочлен Лагранжа.
Інтерполяційний
многочлен може
бути записаний
не тільки у
формі (2). Існують
і інші форми
зображення
інтерполяційного
многочлена,
які можна записати
відразу через
вихідні дані
задачі , тобто
через
![]() не
розв’язуючи
систему (3).
не
розв’язуючи
систему (3).
ТЕОРЕМА. Інтерполяційний многочлен може бути записаний у формі
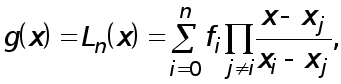 (5)
(5)
яка називається інтерполяційним многочленом Лагранжа .
Доведення . Переконаємось у цьому безпосередньо.
При n=1 маємо
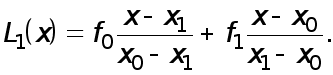 (6)
(6)
Бачимо, що вираз (6) є многочлен першого ступеню, причому підстановкою переконуємося , що
![]()
При n=2
 тобто
маємо многочлен
другого ступеню
і
тобто
маємо многочлен
другого ступеню
і
![]()
Нарешті , для довільного натурального n
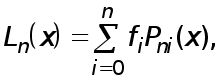 (7)
(7)
де
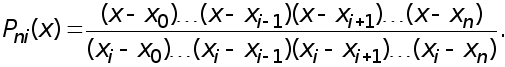 (8)
(8)
Функції
(8) є многочленами
ступеню n.
Отже (7) теж є
алгебраїчним
многочленом
ступеню n
.
Оскільки
![]()
![]() при
при
![]() маємо
маємо
![]()
Функціії (многочлени ) (8) називаються лагранжевими коефіцієнтами .
Зауважимо
, що оскільки
інтерполяційний
многочлен (7)
лінійно залежить
від значень
функції
![]() то
інтерполяційний
многочлен суми
двох функцій
дорівнює сумі
інтерполяційних
многочленів
доданків (коли
вузли інтерполяції
співпадають
) .
то
інтерполяційний
многочлен суми
двох функцій
дорівнює сумі
інтерполяційних
многочленів
доданків (коли
вузли інтерполяції
співпадають
) .
ПОХИБКА ІНТЕРПОЛЯЦІЇ МНОГОЧЛЕНОМ .
Можна записати рівність
![]() (9)
(9)
де
![]() -похибка інтерполяції.
Якщо відносно
функції
f
нічого не відомо,
крім її значень
-похибка інтерполяції.
Якщо відносно
функції
f
нічого не відомо,
крім її значень
![]() у вузлах інтерполяції,
то ніяких корисних
висновків
відносно
у вузлах інтерполяції,
то ніяких корисних
висновків
відносно
![]() зробити неможливо.
Одержимо деякий
вираз похибки
інтерполяції
у припущенні,
що
зробити неможливо.
Одержимо деякий
вираз похибки
інтерполяції
у припущенні,
що
![]() тобто
тобто
![]() -
функція
неперервна
разом зі своїми
-
функція
неперервна
разом зі своїми
![]() похідними,
похідними,
![]() -відрізок,
-відрізок,
що
містить усі
вузли інтерполяції
![]() і точку
і точку
![]() .
.
Введемо позначення
![]() (10)
(10)
ТЕОРЕМА.
Якщо
![]() ,
відрізок
,
відрізок
![]() містить усі
вузли інтерполяції,
то для
містить усі
вузли інтерполяції,
то для
![]() маємо
маємо
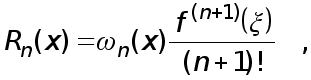 (11)
(11)
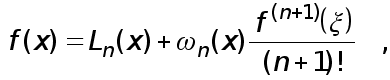 (12)
(12)
де
![]() деяка невідома
точка.
деяка невідома
точка.
Доведення.
Шукаємо
![]() у наступному
вигляді
у наступному
вигляді
![]()
![]()
![]() (13)
(13)
де
![]() деяка
функція, значення
якої у вузлах
інтерполяції
можна задати
які завгодно,
бо
деяка
функція, значення
якої у вузлах
інтерполяції
можна задати
які завгодно,
бо
![]()
Зафіксуємо
довільне
![]() та розглянемо
наступну функцію
від
та розглянемо
наступну функцію
від
![]()
![]() (14)
(14)
Ця
функція внаслідок
(1), (9), (10), (13) дорівнює
нулеві при
![]() та
та
![]() тобто у всякому
випадку у
тобто у всякому
випадку у
![]() точках відрізку
точках відрізку
![]() на якому змінюється
на якому змінюється
![]()
За
теоремою Ролля
![]() дорівнює нулеві
не менше ніж
у
дорівнює нулеві
не менше ніж
у
![]() точках інтервалу
точках інтервалу
![]() дорівнює нулеві
мінімум у n
точках цього
інтервалу і
т. д. Таким чином,
відшукається
хоча б одна
точка
дорівнює нулеві
мінімум у n
точках цього
інтервалу і
т. д. Таким чином,
відшукається
хоча б одна
точка
![]() у якій
у якій
![]() Звідси та з
(14), враховуючи,
що
Звідси та з
(14), враховуючи,
що
![]()
![]()
одержуємо
![]() Отже,
Отже,
![]()
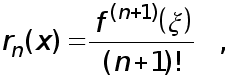
звідки, у відповідності з (13), (9) має місце (11), (12).
З
(12) одержуємо
оцінку похибки
інтерполяції
у точці
![]() :
:
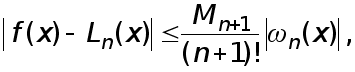 (15)
(15)
та
оцінку максимальної
похибки на
усьому відрізку
![]() :
:
![]()
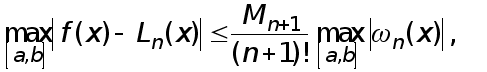 (16)
(16)
де
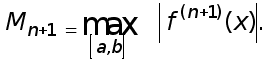
Інтерполяція з рівновіддаленими вузлами.
Розглянемо особливі побудови інтерполяційного многочлена Лагранжа у випадку рівномірного розподілу вузлів.
Нехай
![]() - вузли інтерполяції,
- вузли інтерполяції,
![]() - крок,
- крок,
![]() - задані значення
функції
- задані значення
функції
![]() причому
причому
![]()
Введемо безрозмірну незалежну змінну
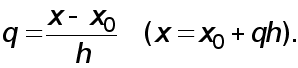
![]()
Тоді
вузлу
![]() відповідає
відповідає
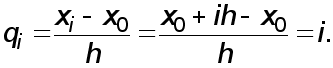
і, окрім того, виконуються співвідношення
![]()
При
цьому інтерполяційний
многочлен
Лагранжа, що
відповідає
випадку
![]() записується
у вигляді
записується
у вигляді ![]()
У загальному випадку інтерполяційний многочлен Лагранжа
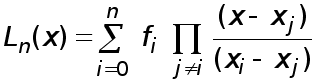
одержить наступний вигляд:
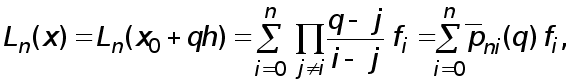
де
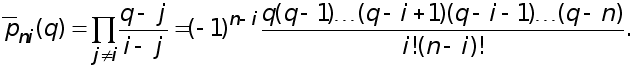
Оскільки
![]()
де
![]()
залишковий член інтерполяційного многочлена може бути поданий у вигляді
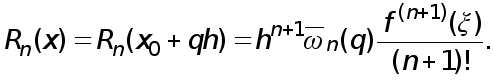
Зауважимо
,що з означення
![]() виходить ,що
зміні змінної
виходить ,що
зміні змінної
![]() на
відрізку
на
відрізку
![]() відповідає
зміна
змінної
відповідає
зміна
змінної
![]() на відрізку
на відрізку
![]()
Тому
оцінку максимальної
похибки інтерполяціі
на відрізку
![]()
можна записати у наступному вигляді :
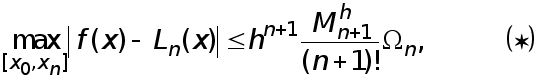
де
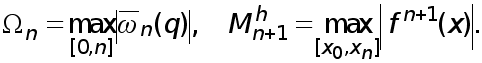
Величина
![]() не залежить
від
не залежить
від
![]() .
Її можна заздалегідь
обчислити чи
оцінити. Зокрема
,
.
Її можна заздалегідь
обчислити чи
оцінити. Зокрема
,
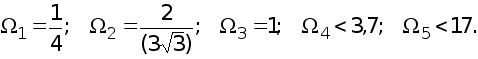
Враховуючи
, що
![]() можна зробити
висновок , що
максимальна
похибка інтерполяціі
на відрізку
можна зробити
висновок , що
максимальна
похибка інтерполяціі
на відрізку
![]() ,
тобто
,
тобто
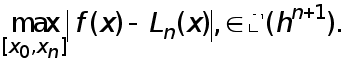
Зауважимо
,що (враховуючи
 )
при зменшенні
кроку
)
при зменшенні
кроку
![]() вдвічі права
частина оцінки
зменшиться
мінімум у
вдвічі права
частина оцінки
зменшиться
мінімум у
![]() разів.
разів.
Виходячи
з підсиленої
оцінки ,що
одержується
з нерівності
![]() ,
у яку замість
,
у яку замість
![]() підставлене
підставлене
![]() ,
вибирають крок
,
вибирають крок
![]() таблиці значень
функції
таблиці значень
функції
![]() на відрізку
на відрізку
![]() з тим щоб забезпечити
задану точність
інтерполяції.
При цьому є ще
можливість
змінювати у
деяких границях
ступінь
з тим щоб забезпечити
задану точність
інтерполяції.
При цьому є ще
можливість
змінювати у
деяких границях
ступінь
![]() інтерполяційного
многочлена.
Якщо функція
інтерполяційного
многочлена.
Якщо функція
![]() достатньо
гладка, то підвищення
достатньо
гладка, то підвищення
![]() спочатку, як
правило, веде
до підвищення
припустимого
спочатку, як
правило, веде
до підвищення
припустимого
![]() , але, з другого
боку, ускладнює
інтерполяцію
і підсилює
вплив неусувних
похибок табличних
значень. На
практиці рідко
використовують
інтерполяцію
з
, але, з другого
боку, ускладнює
інтерполяцію
і підсилює
вплив неусувних
похибок табличних
значень. На
практиці рідко
використовують
інтерполяцію
з
![]()
Зауваження.
При заданому
![]() вузли інтерполяції
вузли інтерполяції
![]()
розташовані
з кроком
![]() ,
доцільно вибирати
з сукупності
усіх вузлів
заданої таблиці
функції так,
щоб точка
,
доцільно вибирати
з сукупності
усіх вузлів
заданої таблиці
функції так,
щоб точка
![]() опинилась як
можна ближче
до середини
відрізку
опинилась як
можна ближче
до середини
відрізку
![]() . Це пов’язано
з тим , що коливання
функцій
. Це пов’язано
з тим , що коливання
функцій
![]() та
та
![]() поблизу середини
згаданого
відрізку менше,
поблизу середини
згаданого
відрізку менше,
ніж у його кінців.
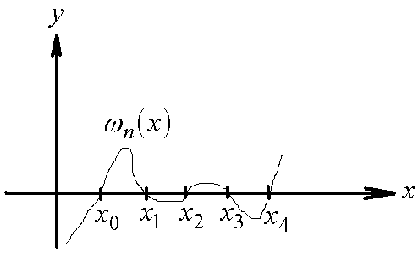
СКІНЧЕННІ ТА ПОДІЛЕНІ РІЗНИЦІ.
Скінченні
різниці.
Нехай
![]() де
де
![]() -
ціле,
-
ціле,
![]() .
Величина
.
Величина
![]() (1)
(1)
називається
скінченною
різницею першого
порядку
функції
![]() у точці
у точці
![]() (з
кроком
(з
кроком
![]() ).
).
Величина
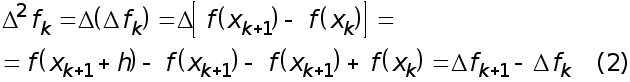 називається
скінченною
різницею другого
порядку функції
називається
скінченною
різницею другого
порядку функції
![]() у точці
у точці
![]() .
.
Взагалі,
скінченна
різниця n-го
порядку
функції
![]() у точці
у точці
![]()
означається рекурентним співвідношенням
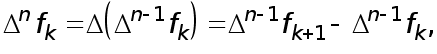 (3)
(3)
де
![]() .
.
При обчисленнях скінченні різниці зручно записувати у вигляді таблиці
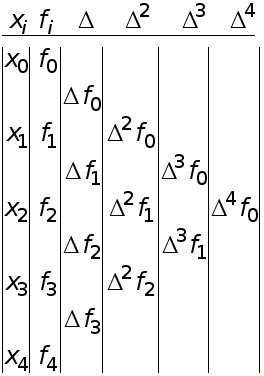
Розглянемо деякі властивості скінченних різниць.
Лема
1.
Якщо
![]() ,
то існує така
точка
,
то існує така
точка
![]() , що
, що
![]() .
(4)
.
(4)
Доведення . При n=1 маємо з формули скінченних приростів
Лагранжа та з (1)
![]()
При
![]() маємо. Позначимо
маємо. Позначимо
![]()
Тоді згідно (2)
![]()
і тому за формулою скінченних приростів Лагранжа
![]() (5)
(5)
Але
![]() .
.
Застосовуючи
ще раз формулу
скінченних
приростів
Лагранжа до
![]() ,
,
маємо
![]() (6)
(6)
де
![]() деяка точка.
З
(5),
(6)
деяка точка.
З
(5),
(6)
виходить
![]()
тобто
твердження
леми при
![]() .
.
Для
![]() лема доводиться
аналогічно.
лема доводиться
аналогічно.
Висновок
з леми 1.
Скінченна
різниця
![]() -го
порядку
алгебраічного
многочлена
-го
порядку
алгебраічного
многочлена
![]() -го
ступеню стала,
тобто не залежить
від
-го
ступеню стала,
тобто не залежить
від
![]() ,
а скінченні
різниці ще
вищих порядків
дорівнюють
нулеві.
,
а скінченні
різниці ще
вищих порядків
дорівнюють
нулеві.
Одне
з практичних
застосувань
скінченних
різниць полягає
у наступному.
Згідно леми
1, якщо
![]() , то
величина
, то
величина
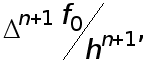 яку можна обчислити
через табличні
значення функції
яку можна обчислити
через табличні
значення функції
![]() за допомогою
формули (3), дорівнює
значенню похідної
за допомогою
формули (3), дорівнює
значенню похідної
![]() у деякій точці
у деякій точці
![]() ,
де
,
де
![]()
Тому
, якщо
![]() мале, то число
мале, то число
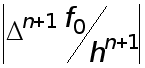 можна наближено
прийняти за
величину
можна наближено
прийняти за
величину
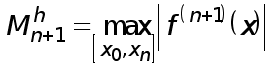
та
використати
в оцінці похибки
інтерполяції
з рівновіддаленими
вузлами. Такою
нестрогою
оцінкою похибки
користуються,
якщо достатньо
складне обчислення
похідної
![]() ,
або, взагалі,
маємо у розпорядженні
тільки табличні
значення n+1
раз
диференційовної
функції.
,
або, взагалі,
маємо у розпорядженні
тільки табличні
значення n+1
раз
диференційовної
функції.
Поділені
різниці.
Нехай
тепер
![]() -довільні
точки (вузли)
осі
-довільні
точки (вузли)
осі
![]() ,
причому
,
причому
![]() при
при
![]() .
.
Значення
![]() функції
функції
![]() у вузлах
називаються
поділеними
різницями
нульового
порядку.
у вузлах
називаються
поділеними
різницями
нульового
порядку.
Число
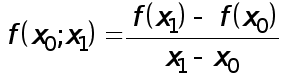 (7)
(7)
називається
поділеною
різницею першого
порядку функції
![]() (відповідно
точкам
(відповідно
точкам
![]() ).
).
Очевидно
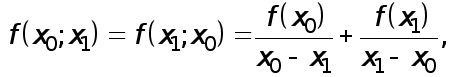 (8)
(8)
тобто
поділена різниця
першого порядку
є симетричною
функцією аргументів
![]() і
і
![]() .
.
Поділена
різниця
![]() -го
порядку
означається
через поділені
різниці
-го
порядку
означається
через поділені
різниці
![]() -го
порядку за
рекурентною
формулою
-го
порядку за
рекурентною
формулою
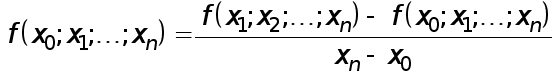 (9)
(9)
При обчисленнях поділені різниці записують у вигляді таблиці
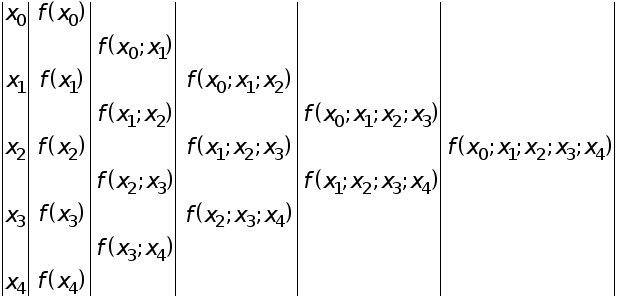 Лема
2.
Поділена різниця
Лема
2.
Поділена різниця
![]() -го
порядку може
бути подана
через
вузлові значення
функції за
формулою
-го
порядку може
бути подана
через
вузлові значення
функції за
формулою
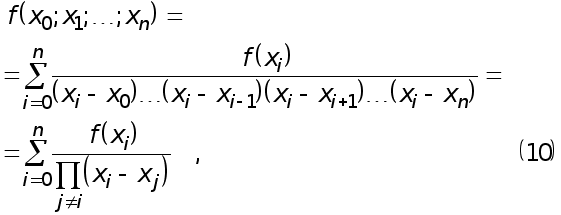
тобто є симетричною функцією своїх аргументів .
Доведення
.
При
![]() твердження
леми виходить
з рівності
(8).
твердження
леми виходить
з рівності
(8).
При
![]() згідно з (9) маємо
згідно з (9) маємо
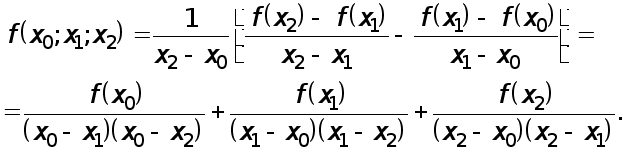
Для
довільного
![]() доведення
проводиться
за індукцією
.
доведення
проводиться
за індукцією
.
Згідно
леми 2 значення
поділеної
різниці не
залежить від
порядку нумерації
![]() вузлів, за якими
вона будується.
Всього маємо
вузлів, за якими
вона будується.
Всього маємо
![]() варіантів
нумерації
вузлів цілими
числами від
0 до
варіантів
нумерації
вузлів цілими
числами від
0 до
![]() .
.
Лема
3.
Якщо
![]() тобто вузли
розміщуються
на осі з сталим
кроком
тобто вузли
розміщуються
на осі з сталим
кроком
![]() то між поділеною
різницею
то між поділеною
різницею
![]() -го
порядку та
скінченною
різницею
-го
порядку та
скінченною
різницею
![]() -го
порядку існує
наступний
зв’язок:
-го
порядку існує
наступний
зв’язок:
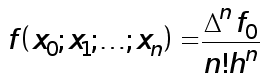 .
(12)
.
(12)
Доведення.
Для
![]() =1
рівність (12)
виходить з (1),
(7). При довільному
=1
рівність (12)
виходить з (1),
(7). При довільному
![]() доведення
провадиться
за індукцією.
При цьому
враховується
той факт, що
при визначенні
кожної наступної
за порядком
скінченної
різниці відбувається
згідно (3) віднімання
попередніх
різниць , а при
обчисленні
наступної
поділеної
різниці згідно
з формулою (9)
провадиться
додаткове
ділення на
величину
доведення
провадиться
за індукцією.
При цьому
враховується
той факт, що
при визначенні
кожної наступної
за порядком
скінченної
різниці відбувається
згідно (3) віднімання
попередніх
різниць , а при
обчисленні
наступної
поділеної
різниці згідно
з формулою (9)
провадиться
додаткове
ділення на
величину
![]() Звідси
й виникає величина
Звідси
й виникає величина
![]() у
знаменнику
правої частини
рівності (12).
у
знаменнику
правої частини
рівності (12).
Лема
4.
Нехай
![]() -мінімальний
відрізок, що
містить вузли
-мінімальний
відрізок, що
містить вузли
![]()
![]() .
Тоді існує така
точка
.
Тоді існує така
точка
![]()
що
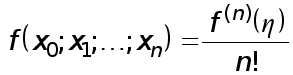 .
(13)
.
(13)
Доведення . Для вузлів, що розміщені з сталим кроком, рівність (13) безпосередньо виходить з лем 1, 3.
Доведення
у загальному
випадку можна
здійснити
наступним
чином. Візьмемо
точку
![]()
![]()
![]() та побудуємо
поділену різницю
та побудуємо
поділену різницю
![]() -го
порядку
-го
порядку
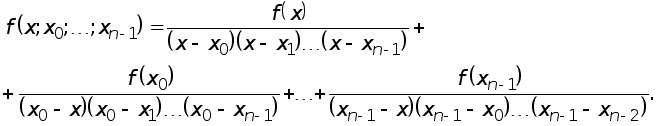 З
цього виразу
можна одержати
З
цього виразу
можна одержати
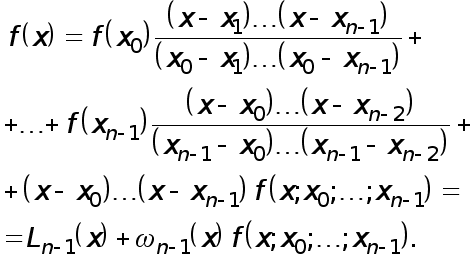
Співставляючи останнє з раніш одержаним виразом для похибки
![]() ,
одержуємо
,
одержуємо
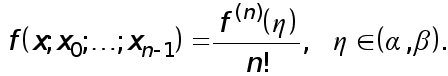
Покладаючи
тепер
![]() ,
одержимо (13).
,
одержимо (13).
Висновок
з леми 4.
Поділена різниця
![]() -го
порядку від
алгебраічного
многочлена
-го
порядку від
алгебраічного
многочлена
![]() -го
ступеню має
стале значення,
що не залежить
від вузлів
-го
ступеню має
стале значення,
що не залежить
від вузлів
![]() а поділені
різниці ще
вищих порядків
дорівнюють
нулеві.
а поділені
різниці ще
вищих порядків
дорівнюють
нулеві.
Скінченні і поділені різниці мають різноманітні застосування. Далі розглянемо їх використання для побудови інтерполяційних многочленів.
Інтерполяційний многочлен Ньютона .
Нехай
![]() -довільні
вузли, що не
співпадають
і у яких відомі
значення функції
-довільні
вузли, що не
співпадають
і у яких відомі
значення функції
![]() .
.
Лема
1. Алгебраїчний
многочлен
![]() -го
ступеню
-го
ступеню
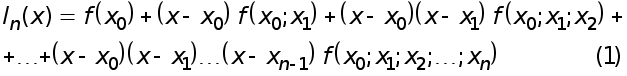 є
інтерполяційним,
тобто
є
інтерполяційним,
тобто
![]() (2)
(2)
Доведення.
Поперш за все
зауважимо,що
поділені різниці
![]() є числа (не залежать
від
є числа (не залежать
від
![]() ), і тому функція
(1) дійсно є алгебраїчний
многочлен
), і тому функція
(1) дійсно є алгебраїчний
многочлен
![]() -го
ступеню. Доведемо
(2) при
-го
ступеню. Доведемо
(2) при
![]() .
Маємо
.
Маємо ![]()
Очевидно
![]() ,
,
![]() Тобто
при n=1
рівності
(2) справедливі.
Тобто
при n=1
рівності
(2) справедливі.
Доведемо
(2) при
![]() .
Маємо
.
Маємо
![]()
![]()
![]()
При
![]() рівності (2)
доведені .
рівності (2)
доведені .
При
довільному
натуральному
![]() рівності (2)
доводяться
за індукцією.
рівності (2)
доводяться
за індукцією.
Многочлен (1) називається інтерполяційним многочленом Ньютона для нерівних проміжків .
Згідно
теоремі єдності
він тотожньо
співпадає з
інтерполяційним
многочленом
Лагранжа, тобто
![]() Таким чином
ми маємо різні
записи інтерполяційного
многочлена.Залишковий
член інтерполяційного
многочлена
Ньютона той
же, що і інтерполяційного
многочлена
Лагранжа, тобто
всюди в оціночних
рівностях і
нерівностях
можна замінити
Таким чином
ми маємо різні
записи інтерполяційного
многочлена.Залишковий
член інтерполяційного
многочлена
Ньютона той
же, що і інтерполяційного
многочлена
Лагранжа, тобто
всюди в оціночних
рівностях і
нерівностях
можна замінити
![]() на
на
![]()
У
інтерполяційного
многочлена
Лагранжа видно
його явну залежність
від кожного
значення функції
![]() Це у багатьох
випадках буває
корисним. Але
при зміні
Це у багатьох
випадках буває
корисним. Але
при зміні
![]() інтерполяційний
многочлен
Лагранжа треба
будувати заново.
У цьому є його
недолік.
інтерполяційний
многочлен
Лагранжа треба
будувати заново.
У цьому є його
недолік.
Інтерполяційний
многочлен
Лагранжа (1) містить
не значення
функції
![]() ,
а її поділені
різниці. При
зміні степеню
,
а її поділені
різниці. При
зміні степеню
![]() у інтерполяційного
многочлена
Ньютона треба
добавити або
відкинути
відповідну
кількість
стандартних
доданків. Це
зручно на практиці.
у інтерполяційного
многочлена
Ньютона треба
добавити або
відкинути
відповідну
кількість
стандартних
доданків. Це
зручно на практиці.
Випадок
равновіддалених
вузлів.
Нехай
![]()
![]() Тоді,
враховуючи
зв’язок
поділеної
різниці із
скінченною
різницею
Тоді,
враховуючи
зв’язок
поділеної
різниці із
скінченною
різницею
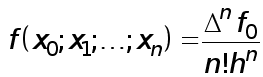
і вводячи безрозмірну змінну
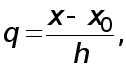
інтерполяційний многочлен (1) можна переписати у вигляді
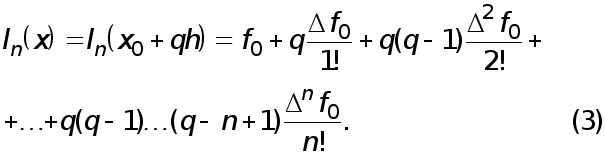
Цей многочлен називається інтерполяційним многочленом Ньютона для інтерполяції вперед.
У
ньому початок
відліку знаходиться
у крайньому
вузлі
![]() ,
а використані
скінченні
різниці йдуть
у таблиці різниць
від
,
а використані
скінченні
різниці йдуть
у таблиці різниць
від
![]() вправо униз.
Інтерполяційний
многочлен (3)
зручно використовувати
на початку
таблиці.
вправо униз.
Інтерполяційний
многочлен (3)
зручно використовувати
на початку
таблиці.
Інтерполяційний
многочлен
з
вулами
![]() ,
,
,де
![]() ,
має вигляд
,
має вигляд
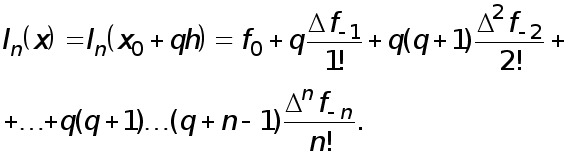 (4)
(4)
і називається інтерполяційним многочленом Ньютона для інтерполяції назад.
У
ньому початок
відліку
![]() розташований
у крайньому
правому вузлі
розташований
у крайньому
правому вузлі
![]() ,
а вікористані
скінченні
різниці йдуть
у таблиці від
,
а вікористані
скінченні
різниці йдуть
у таблиці від
![]() вправо угору
.
вправо угору
.
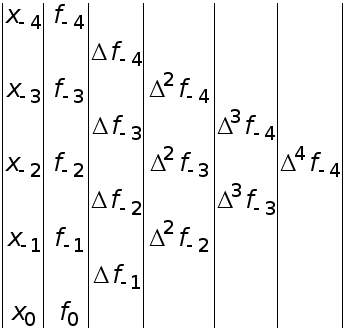
Інтерполяційний многочлен (4) зручно використовувати при інтерполяції у кінці таблиці.
Якщо
при заданому
![]() у таблиці значень
функції
у таблиці значень
функції
![]() з кроком
з кроком
![]()
маємо
достатню кількість
вузлів з кожного
боку від
![]() ,
то доцільно
вузли інтерполяції
,
то доцільно
вузли інтерполяції
![]() вибирати так,
щоб точка
вибирати так,
щоб точка
![]() опинилась як
можна ближче
до середини
мінімального
відрізку, що
містить вузли.
При цьому
інтерполяційний
многочлен можна
будувати по-
різному.
опинилась як
можна ближче
до середини
мінімального
відрізку, що
містить вузли.
При цьому
інтерполяційний
многочлен можна
будувати по-
різному.
Найбільш
істотньо задати
інтерполяційний
многочлен у
вигляді (1), де
за
![]() береться найближчий
до
береться найближчий
до
![]() вузол, далі за
вузол, далі за
![]() приймається
найближчий
до
приймається
найближчий
до
![]() вузол, що міститься
з протилежного
від
вузол, що міститься
з протилежного
від
![]() боку, ніж
боку, ніж
![]() .
Наступні вузли
призначаються
по черзі з різних
боків від
.
Наступні вузли
призначаються
по черзі з різних
боків від
![]() ,
що містяться
як можливо
ближче до
,
що містяться
як можливо
ближче до
![]() .
При токому
виборі вузлів
доданки, що
слідують один
за одним у виразі
(1), як правило,
спадають, якщо
.
При токому
виборі вузлів
доданки, що
слідують один
за одним у виразі
(1), як правило,
спадають, якщо
![]() мале, а
мале, а
![]() невелике.
невелике.
Можливо також у розглянутому випадку використовувати інтерполяційні многочлени (3), (4), а також інтерполяційний многочлен Лагранжа.
На закінчення зазначимо, що залишковий член многочлена (3) має той же вигляд, що і у випадку інтерполяційного многочлена Лагранжа з рівновіддаленими вуздами, тобто
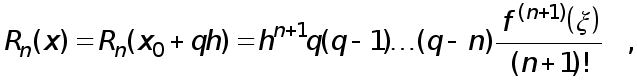 а
залишковий
член інтерполяційного
многочлена
(4) може бути подано
у вигляді
а
залишковий
член інтерполяційного
многочлена
(4) може бути подано
у вигляді
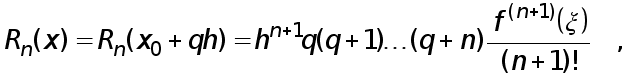 де
де
![]() -похідна від
-похідна від
![]() ,
,
![]() -деяка
точка мінімального
відрізку, що
містить вузли
інтерполяції
-деяка
точка мінімального
відрізку, що
містить вузли
інтерполяції
![]() і точку
і точку
![]() .
.
Згідно
лемі, у якій
показано, що
![]() та при умові,
що
та при умові,
що
![]() мале, а функція
мале, а функція
![]() достатньо
гладка, поточний
доданок у виразі
(3) інтерполяційного
многочлена
Ньютона приблизно
дорівнює похибці
інтерполяції
многочленом,
побудованим
з усіх попередніх
доданків. Це
зауваження
стосується
й до інтерполяційного
многочлена
(4) для інтерполяції
назад.
достатньо
гладка, поточний
доданок у виразі
(3) інтерполяційного
многочлена
Ньютона приблизно
дорівнює похибці
інтерполяції
многочленом,
побудованим
з усіх попередніх
доданків. Це
зауваження
стосується
й до інтерполяційного
многочлена
(4) для інтерполяції
назад.
МЕТОД ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.
Основная идея метода. Может оказаться, что система
Ax=f (1)
имеет единственное решение, хотя какой-либо из угловых миноров матрицы А равен нулю. В этом случае обычный метод Гаусса оказывается непригодным, но может быть применен метод Гаусса с выбором главного элемента.
Основная
идея метода
состоит в том,
чтобы на очередном
шаге исключать
не следующее
по номеру
неизвестное,
а то
неизвестное,
коэффициент
при котором
является наибольшим
по модулю. Таким
образом, в качестве
ведущего элемента
здесь выбирается
главный,
т.е. наибольший
по модулю элемент.
Тем самым, если
![]() ,
то в процессе
вычислений
не будет происходить
деление на
нуль.
,
то в процессе
вычислений
не будет происходить
деление на
нуль.
Различные варианты метода Гаусса с выбором главного элемента проиллюстрируем на примере системы из двух уравнений
![]() (2)
(2)
![]()
![]()
![]()
![]() Предположим,
что
Предположим,
что
![]() .
Тогда на первом
шаге будем
исключать
переменное
.
Тогда на первом
шаге будем
исключать
переменное
![]() .
Такой прием
эквивалентен
тому, что система
(2) переписывается
в виде
.
Такой прием
эквивалентен
тому, что система
(2) переписывается
в виде
![]() (3)
(3)
![]()
и к (3) применяется первый шаг обычного метода Гаусса. Указанный способ исключения называется методом Гаусса с выбором главного элемента по строке. Он эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация переменных.
Применяется
также метод
Гаусса с выбором
главного элемента
по столбцу.
Предположим,
что
![]() .
Перепишем
систему (2) в
виде
.
Перепишем
систему (2) в
виде
![]()
![]()
и к новой системе применим на первом шаге обычный метод Гаусса. Таким образом, метод Гаусса с выбором главного элемента по столбцу эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация уравнений.
Иногда применяется и метод Гаусса с выбором главного элемента по всей матрице, когда в качестве ведущего выбирается максимальный по модулю элемент среди всех элементов матрицы системы.
Матрицы перестановок. Ранее было показано, что обычный метод Гаусса можно записать в виде
![]()
![]()
где
![]() -элементарные
нижние треугольные
матрицы. Чтобы
получить аналогичную
запись метода
Гаусса с выбором
главного элемента,
необходимо
рассмотреть
матрицы перестановок.
-элементарные
нижние треугольные
матрицы. Чтобы
получить аналогичную
запись метода
Гаусса с выбором
главного элемента,
необходимо
рассмотреть
матрицы перестановок.
ОПРЕДЕЛЕНИЕ 1. Матрицей перестановок Р называется квадратная матрица, у которой в каждой строке и в каждом столбце только один элемент отличен от нуля и равен единице.
ОПРЕДЕЛЕНИЕ
2.
Элементарной
матрицей перестановок
![]() называется
матрица, полученная
из единичной
матрицы перестановкой
называется
матрица, полученная
из единичной
матрицы перестановкой
![]() к-й
и l-й
строк.
к-й
и l-й
строк.
Например, элементарными матрицами перестановок третьего порядка являются матрицы
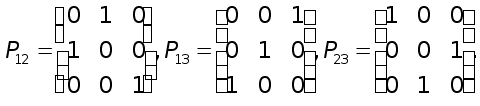
Можно отметить следующие свойства элементарных матриц перестановок, вытекающие непосредственно из их определения .
Произведение двух (а следовательно, и любого числа) элементарных матриц перестановок является матрицей перестановок (не обязательно элементарной).
Для любой квадратной матрицы А матрица
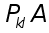 отличается
от А
перестановкой
к-й
и
l-й
строк.
отличается
от А
перестановкой
к-й
и
l-й
строк.Для любой квадратной матрицы А матрица
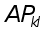 отличается
от А
перестановкой
к-го
и l-го
столбцов.
отличается
от А
перестановкой
к-го
и l-го
столбцов.
Применение элементарных матриц перестановок для описания метода Гаусса с выбором главного элемента по столбцу можно пояснить на следующем примере системы третьего порядка:
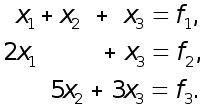 (4)
(4)
Система имеет вид (1), где
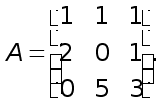 (5)
(5)
Максимальный элемент первого столбца матрицы А находится во второй строке. Поэтому надо поменять местами вторую и первую строки и перейти к эквивалентной системе
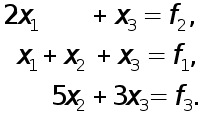 (6)
(6)
Систему (6) можно записать в виде
![]() (7)
(7)
т.е. она получается из системы (4) путем умножения на матрицу
перестановок
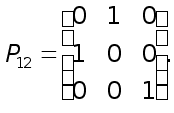
Далее, к системе (6) надо применить первый шаг обычного метода исключения Гаусса. Этот шаг эквивалентен умножению системы (7) на элементарную нижнюю треугольную матрицу
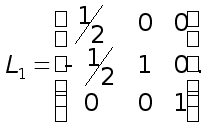
В результате от системы (7) перейдем к эквивалентной системе
![]() (8)
(8)
или в развернутом виде
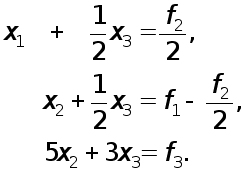 (9)
(9)
Из последних
двух уравнений
системы (9) надо
теперь исключить
переменное
![]() .
Поскольку
максимальным
элементом
первого столбца
укороченной
системы
.
Поскольку
максимальным
элементом
первого столбца
укороченной
системы
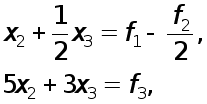 (10)
(10)
является элемент второй строки, делаем в (10) перестановку строк и тем самым от системы (9) переходим к эквивалентной системе
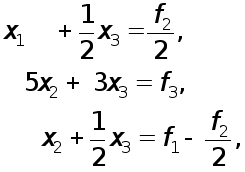 (11)
(11)
которую можно записать в матричном виде как
![]() .
(12)
.
(12)
Таким образом система (12) получена из (8) применением элемен-тарной матрицы перестановок
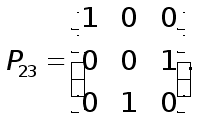
Далее к системе (11) надо применить второй шаг исключения обычного метода Гаусса. Это эквивалентно умножению системы (11) на элементарную нижнюю треугольную матрицу
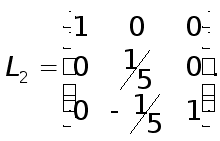
В результате получим систему
![]() (13)
(13)
или
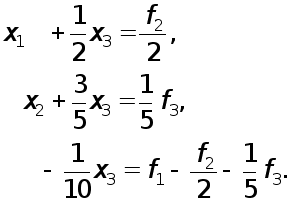 (14)
(14)
Заключительный шаг прямого хода метода Гаусса состоит в замене последнего уравнения системы (14) уравнением
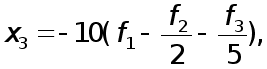
что эквивалентно умножению (13) на элементарную нижнюю треугольную матрицу
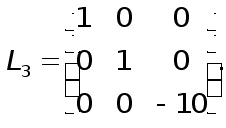
Таким образом, для рассмотренного примера процесс исключения Гаусса с выбором главного элемента по столбцу записывается в
виде
![]() (15)
(15)
По построению матрица
![]() (16)
(16)
является верхней треугольной матрицей с единичной главной диагональю.
Отличие
от обычного
метода Гаусса
состоит в том,
что в качестве
сомножителей
в (16) наряду с
элементарными
треугольными
матрицами
![]() могут
присутствовать
элементарные
матрицы перестановок
могут
присутствовать
элементарные
матрицы перестановок
![]() .
.
Покажем еще, что из (16) следует разложение
PA=LU, (17)
где L -нижняя треугольная матрица, имеющая обратную, P - матрица перестановок.
Для этого найдем матрицу
![]() (18)
(18)
По свойству
2) матрица
![]() получается
из матрицы
получается
из матрицы
![]() перестановкой
второй и третьей
строк,
перестановкой
второй и третьей
строк,
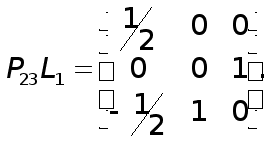
Матрица
![]() согласно
свойству 3)
получается
из
согласно
свойству 3)
получается
из
![]() перестановкой
второго и третьего
столбцов
перестановкой
второго и третьего
столбцов
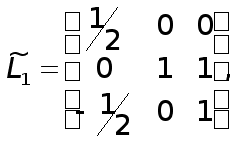
т.е.
![]() -нижняя
треугольная
матрица, имеющая
обратную.
-нижняя
треугольная
матрица, имеющая
обратную.
Из (18), учитывая
равенство
![]() ,
получим
,
получим
![]() (19)
(19)
Отсюда и из (16) видно, что
![]()
где обозначено
![]() .
Поскольку
Р-матрица
перестановок
и L-нижняя
треугольная
матрица, свойство
(17) доказано. Оно
означает, что
метод Гаусса
с выбором главного
элемента по
столбцу эквивалентен
обычному методу
Гаусса, примененному
к матрице РА,
т.е. к системе,
полученной
из исходной
системы перестановкой
некоторых
уравнений.
.
Поскольку
Р-матрица
перестановок
и L-нижняя
треугольная
матрица, свойство
(17) доказано. Оно
означает, что
метод Гаусса
с выбором главного
элемента по
столбцу эквивалентен
обычному методу
Гаусса, примененному
к матрице РА,
т.е. к системе,
полученной
из исходной
системы перестановкой
некоторых
уравнений.
Общий вывод. Результат, полученный ранее для очень частного примера, справедлив и в случае общей системы уравнений (1).
А именно, метод Гаусса с выбором главного элемента по столбцу можно записать в виде
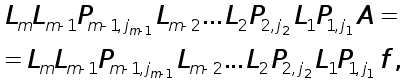 (20)
(20)
где
![]() -
элементарные
матрицы перестановок
такие, что
-
элементарные
матрицы перестановок
такие, что
![]() и
и
![]() -элементарные
нижние треугольные
матрицы.
-элементарные
нижние треугольные
матрицы.
Отсюда, используя соотношения перестановочности, аналогичные (19), можно показать, что метод Гаусса с выбором главного элемента эквивалентен обычному методу Гаусса, примененному к системе
PAx=Pf, (21)
где Р - некоторая матрица перестановок.
Теоретическое обоснование метода Гаусса с выбором главного элемента содержится в следующей теореме.
ТЕОРЕМА
1. Если
![]() то
существует
матрица перестано-
то
существует
матрица перестано-
вок Р такая, что матрица РА имеет отличные от нуля угловые ми-
норы.
Доказательство в п.4.
СЛЕДСТВИЕ.
Если
![]() то
существует
матрица престана-
то
существует
матрица престана-
вок Р такая, что справедливо разложение
РА=LU, (22)
где L- нижняя треугольная матрица с отличными от нуля диагональными элементами и U- верхняя треугольная матрица с единичной главной диагональю. В этом случае для решения системы (1) можно применять метод Гаусса с выбором главного элемента.
4. Доказательство теоремы 1. Докажем теорему индукцией по числу m -порядку матрицы А.
Пусть m=2, т.е.
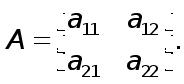
Если
![]() то утверждение
теоремы выполняется
при Р=Е,
где Е
- единичная
матрица второго
порядка. Если
то утверждение
теоремы выполняется
при Р=Е,
где Е
- единичная
матрица второго
порядка. Если
![]() ,
то
,
то
![]() ,
т.к.
,
т.к.
![]() При
этом у матрицы
При
этом у матрицы
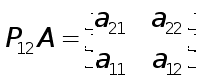
все угловые миноры отличны от нуля.
Пусть утверждение теоремы верно для любых квадратных матриц порядка m-1. Покажем, что оно верно и .для матриц порядка m. Разобьем матрицу А порядка m на блоки
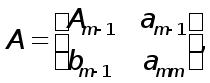
где
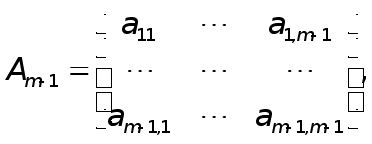
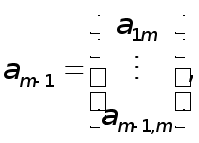
![]()
Достаточно
рассмотреть
два случая :![]() и
и
![]() .
В первом случае
по предположению
индукции существует
матрица перестановок
.
В первом случае
по предположению
индукции существует
матрица перестановок
![]() порядка
m-1
такая,
что
порядка
m-1
такая,
что
![]() имеет
отличные от
нуля угловые
миноры. Тогда
для матрицы
перестановок
имеет
отличные от
нуля угловые
миноры. Тогда
для матрицы
перестановок
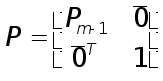
имеем
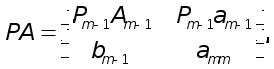
причем
![]() .
Тем самым все
угловые миноры
матрицы РА
отличны
от нуля.
.
Тем самым все
угловые миноры
матрицы РА
отличны
от нуля.
Рассмотрим
второй случай,
когда![]() . Т.к.
. Т.к.![]() , найдется хотя
бы один отличный
от нуля минор
порядка m-1
матрицы
А,
полученный
вычеркиванием
последнего
столбца и какой-либо
строки. Пусть,
например,
, найдется хотя
бы один отличный
от нуля минор
порядка m-1
матрицы
А,
полученный
вычеркиванием
последнего
столбца и какой-либо
строки. Пусть,
например,
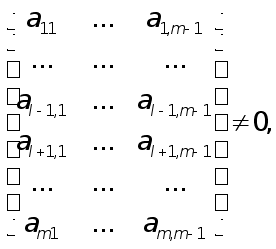
где
![]() .
.
Переставляя
в матрице А
строки
с номерами l
и m,
получим
матрицу
![]() ,
у
которой угловой
минор порядка
m-1 имеет
вид
,
у
которой угловой
минор порядка
m-1 имеет
вид
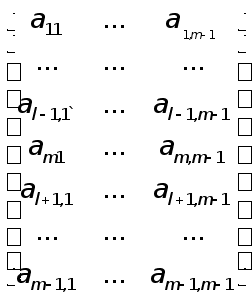
и отличается от (23) только перестановкой строк. Следовательно, этот минор не равен нулю и мы приходим к рассмотренному выше случаю.
Теорема доказана.
