Реферат: Фракталы и автоколебания в геоморфосистемах

Ю.В. Лялин, А.В. Поздняков

Институт оптического мониторинга СО РАН, Томск

Развитие целостных систем, независимо от их природы, обеспечивается за счет поступления энергии и вещества из среды и выделения их в среду. Динамика разницы расходов вещества и энергии в этих двух потоках в течение времени и определяет развитие системы, а установление баланса вещества и энергии на входе и выходе системы характеризует ее динамически равновесный режим. Таким образом, формирование, развитие и самоорганизация целостных систем осуществляется через диалектическое взаимодействие двух потоков вещества и энергии противоположной направленности.

Потоки энергии и вещества, формирующие природные системы, названы [1, 2] F-потоками, а потоки, вызывающие их деградацию, - D-потоками. Действие F-потоков, формирующих систему, необратимо направлено к росту показателей, характеризующих систему: размеры, объем, а действие D-потоков приводит к их уменьшению [1, 2]. Величина D-потока (расход энергии и вещества в нем) монотонно зависит от параметров системы: чем больше размеры системы, создающейся вследствие действия F-потока, тем больше величина D-потока; и наоборот, с уменьшением размеров системы уменьшается и величина D-потока.

Рост размеров систем, по мере приближения к своим предельным характеристикам, асимптотически затухает, в силу того, что величина расхода в D-потоке стремится к таковой в F-потоке. Теоретически в конечном варианте развития системы должен устанавливаться баланс расходов вещества и энергии в обоих потоках, характеризующий состояние динамического (термодинамического) равновесия, или предельного цикла системы. Практически же, в силу постоянно меняющихся условий равзития системы и, следовательно, изменения расходов вещества в F- и D-потоках, это состояние никогда не достигается, при объективном к нему стремлении.

Фракталы в геоморфосистемах. В геоморфосистемах роль F-потока играет эндогенный поток вещества, создающий первичную наклонную поверхность. Она подвергается эрозионному расчленению, в результате чего создается экзогенный литопоток вещества (D-поток) и формируются склоны второй генерации. Эти склоны снова расчленяются, с образованием склонов последующей генерации, и так далее. При этом крутизна склонов последующей генерации растет следующим образом:

где a - крутизна склона; j – уклон тальвега, базиса эрозии.

Поскольку рельеф в процессе эрозионного расчленения сохраняет подобие, то его можно считать фрактальным.

Рассмотрим пример геоморфологического фрактального множества. Его построение начинается с равнобедренного треугольника с углом при основании - это 0-е поколение. Далее на каждой боковой стороне строится равнобедренный треугольник с таким же углом. В результате получается следующее поколение. При бесконечном повторении этого процесса получим фрактальное множество.

Важным свойством фрактальных множеств является дробная размерность. По определению, размерность Хаусдорфа равна D=log(N)/log(f), где N - число частей, а f показывает, во сколько раз целое больше части. Так как при построении фрактальной поверхности рельефа на каждом последующем шаге площадь треугольника, характеризующего поперечное сечение формы рельефа, в 4 cos2(α) меньше площади предыдущей формы, из которой он получен, то для него N = 2, f = и, следовательно, размерность D Хаусдорфа полученного множества равна D = log(2)/log.

Рис. 1. Фрактальная характеристика эрозионно расчленного рельефа из 7 поколений множества

Вследствие фрактального характера процесса эрозионного расчленения, площадь поверхности рельефа можно найти по формуле:

, (1)

где - площадь поверхности формы рельефа, не подвергшейся эрозионному расчленению, величина m>1 зависит от размерности границы поверхности.

Таким образом, процесс эрозионного расчленения и роста площади поверхности, а следовательно, и денудации является нелинейным, и в силу этих причин в геоморфосистеме проявляются автоколебания.

Механизм возникновения автоколебаний в геоморфосистемах. Появление F-потока вещества и формирование системы вызывает через некоторое время появление D-потока. С ростом размеров системы мультипликативно нарастает и D-поток (за счет увеличения площади S поверхности). Когда величина D-потока превысит величину F-потока, рост размеров системы (объема, высоты и пр.) прекратится и начнется их уменьшение. По мере уменьшения размеров системы будут снижаться расходы вещества и в D-потоках. Когда его величина станет меньше расходов в F-потоке, снова начнется рост размеров системы. Таким образом, динамика системы имеет колебательный характер. Отметим, что обычно, вследствие различных причин, система "проскакивает" положение равновесия (то есть момент равенства F и D-потоков), и в ней возникают автоколебания даже при постоянной величине F-потока.

Алгоритм формирования рельефа [3] представлен в блок-схеме (рис. 2).

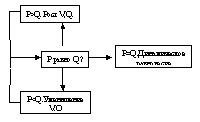
Рис. 2. блок-схема алгоритма формирования рельефа в результате взаимодействия F- и D-потоков V-объём вещества, заключённого в формах рельефа; P и Q - объёмы вещества, поступающего соответственно в эндогенном (F-) и экзогенном (D-) литопотоках

Для исследования связи между механизмами образования фракталов и возникновения автоколебаний в некоторой системе, необходимо построить ее математическую модель. Математической моделью реальной системы будем считать динамическую систему, понимаемую как отображение S(t,x) фазового пространства, или пространства состояний в себя и задаваемую уравнением вида. Его решения есть кривые в фазовом пространстве, или фазовые траектории.

Как было установлено [4], физическому понятию автоколебаний соответствует математическое понятие предельного цикла. Можно показать, что фазовые траектории в его окрестностях имеют вид раскручивающихся или скручивающихся спиралей, подобных изображенной на рис 3, наматывающихся на некоторую замкнутую кривую, которая и называется предельным циклом.

Рис. 3. Предельный цикл и спиралевидныая фазовая траектория

Однако эти спирали лишь стремятся к предельному циклу, бесконечно близко к нему приближаясь, но не пересекая его.

Таким образом, предельный цикл самоподобен, а поведение автоколебательной системы фрактально.

В силу того, что скорость роста размеров системы зависит от разницы F(t)-D(t), динамику геоморфосистем, как и других подобных систем, развивающихся на таких же принципах, можно описывать уравнением:

, (2)

где - размеры системы; и- функции, выражающие скорость изменения размеров системы.

Если в качестве размеров системы брать объем вещества, заключенного в формах рельефа, а в качестве F- и D-потоков - объемы эндогенного и денудируемоего материала соответственно, получим из (2) следующую систему уравнений, описывающую динамику рельефа 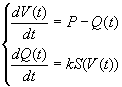[3]:

(3)

где V – объем вещества, заключенного в форме рельефа, м3; P – объем эндогенного материала, м3/год; Q – объем денудируемоего материала, м3/год; к – коэффициент денудации, м3 с м2/год;

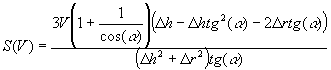– площадь поверхности формы рельефа с объемом V, м3;– крутизна формы рельефа, рад.; - прирост высоты, м; - прирост площади основания единичной ширины, м2.

Если крутизна форм рельефа, прирост высоты и площадь основания постоянны, то система уравнений (3) линейна, и в ее фазовом пространстве не может существовать предельный цикл. Однако с учетом фрактального характера процесса эрозионного расчленения, система уравнений модели приобретает вид:

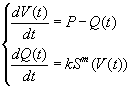(4)

Система уравнений (4) является нелинейной, и в ее фазовом пространстве может существовать предельный цикл [4]. Исследование данной модели возможно с использованием численных методов. Заменяя в (4) дифференциальный оператор разностным, получим следующую разностную схему:

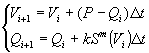(5)

Результаты расчетов с применением (5) показывают, что положение равновесия системы (4) является неустойчивым, и фазовые траектории в его окрестности имеют вид раскручивающихся спиралей. Так как расход вещества в эндогенном литопотоке есть конечная величина, а объем денудируемоего материала не может быть меньше нуля, то эти спирали не могут раскручиваться в бесконечность. Они обязательно начнут наматываться на некоторую замкнутую кривую и примут вид, подобный изображенному на рис 3.

Таким образом, в фазовом пространстве системы (4) существует предельный цикл, и в геоморфосистеме, моделью которой она является, могут возникать автоколебания.

Следует подчеркнуть, что именно вследствие фрактального характера процесса эрозионного расчленения система (4) становится нелинейной, и этим обусловливается возможность возникновения автоколебаний в геоморфосистемах и в целом движение системы к состоянию динамического равновесия. Достигнув его, она, в силу изменения баланса расходов вещества в литопотоках, уходит от него, с тем чтобы опять, по истечении некоторого времени, возвратиться. Динамику системы в таком состоянии можно сравнить с динамикой спиральной пружины маятника в часах – она то сжимается, то разжимается, находясь в заданных пределах. Применительно к рельфу, этот предел устанавливается F-потоком.

В реальности состояние динамического равновесия никогда не достигается, хотя стремление к нему объективно, оно, можно сказать, имманентно присуще всем целостным самоорганизующимся образованиям.

Литература:

Поздняков А.В. Динамическое равновесие в рельефообразовании. – М.: Наука, 1988. – 207 с.

Поздняков А.В. Стратегия российских реформ . – Томск: Спектр, 1998. – 324 с.

Поздняков А.В., Лялин Ю.В., Тихоступ Д.М. Формирование поверхности равновесия и фрактальные соотношения в эрозионном расчленении // Самоорганизация геоморфосистем (Пробл. самоорганизации. Вып. 3). – Томск: ТНЦ СО РАН, 1996. – С. 36-48.

Понтрягин Л.С. Обыкновенные дифференциальные уравнения. - М.: Наука, 1982. – 331 с.