
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Реферат: Математическая модель взаимодействия подсистем производства сельхозпродуктов в районных АПК
Реферат: Математическая модель взаимодействия подсистем производства сельхозпродуктов в районных АПК
1.Оглавление.
1. Оглавление. 1
2. Введение. Постановка задачи. 2
3. Анализ производства продуктов в районных АПК. 6
4. Использование преобразования Лапласа для моделирования экономических процессов 16
4.1. Пропорциональное (усилительное) звено 16
4.2. Дифференцирующее и интегрирующее (накопительнное) звенья 17
4.3. Звенья запаздывания 17
5. Динамическая модель. 20
5.1. Производственная функция и производственные фонды. 20
5.2. Модель развития отдельного предприятия. 21
5.3. Динамика взаимодействия производства сельхозкооперативов и личных хозяйств членов этих кооперативов. 22
6. Модель взаимодействия хозяйств сельхозкооперативов и личных хозяйств членов кооперативов. 26
6.1. Структурная схема 26
6.2. Производственные взаимосвязи. 29
6.3. Взаимодействие сельхозпредприятий и личных хозяйств для частного случая производственной функции. 31
7. Заключение. 35
8. Литература 36
2.Введение. Постановка задачи.
Задачей настоящей работы является разработка модели взаимодействия двух основных подсистем производства продуктов сельского хозяйства в районных АПК, использование которой позволит выработать предложения по методам целенаправленного воздействия на подсистемы для достижения требуемого (желаемого) состояния системы.
Актуальность подобной задачи определяется необходимостью сосредоточения усилий управляющих структур всех уровней на обеспечение научно обоснованных решений вывода сельского хозяйства страны из кризиса, и, соответственно, обеспечение продовольственной безопасности России. Под продовольственной безопасностью страны обычно понимают отсутствие самой возможности голода или длительного недоедания, что достигается поддержанием показателей продовольственного снабжения населения на уровне, гарантирующем устойчивую экономическую и социально-политическую стабильность общества при достаточном самообеспечении и наличии средств для импорта продуктов. Причем в случае осложнений и отказа от импорта уровень обеспечения населения основными продуктами должен оставаться достаточным. Известно два основных показателя продовольственной безопасности:
Размер переходящих запасов,
Производство зерна на душу населения.
Значение этих показателей в России сегодня явно неудовлетворительно.
Основные причины кризиса сельского хозяйства в России – серьезное отставание сельского хозяйства по производительности труда, внедрению современных технологий, полезной отдачи вкладываемых средств. Согласно проведенным оценкам средняя продуктивность всех факторов производства – труда, земли, машин, удобрений, животных – в России в два раза ниже, чем в сходных по климатическим условиям районах Канады.
Все кризисные явления характерно и для Тверской области.
Поиск оптимальных управлений, целенаправленного воздействия на систему может быть успешен при использовании системного подхода, в том числе при рассмотрении любой системы в динамике и взаимосвязей элементов, составляющих систему с учетом взаимодействия системы с окружающей средой. В этой связи одним из основных этапов поиска целенаправленных управлений является изучение структуры системы, реальных связей между элементами системы. В [8] приводится следующий известный тезис кибернетики: «Существуют законы природы, которым подчиняется поведение больших многосвязных систем любого характера: биологических, технических, социальных и экономических. Эти законы относятся к процессам саморегуляции и самоорганизации и выражают именно те «руководящие принципы», которые определяют рост и устойчивость, обучение и регулирование, адаптацию и эволюцию систем. На первый взгляд, совершенно различные системы с точки зрения кибернетики совершенно одинаковы, поскольку они демонстрируют так называемое жизнеспособное поведение, целью которого является выживание. Подобное поведение системы определяется не столько процессами, происходящими в ней самой, или теми значениями, которые принимают даже важнейшие из ее параметров, но, в первую очередь, ее динамической структурой, как способом организации взаимодействия отдельных частей единого целого. Важнейшими элементами структуры системы являются контуры обратных связей, которые и обеспечивают саморегулирование, самообучение и самоорганизацию системы. Основные результаты деятельности системы – это ее исходы. Для того чтобы исходы отвечали нашим целям, необходимо соответствующим образом организовать структуру системы».
Следуя этому тезису, производство продуктов в сельском хозяйстве района рассматривается в настоящей работе как деятельность системы, состоящей из взаимосвязанных подсистем. Особое внимание уделяется реальным связям между подсистемами, возможности регулировать эти связи. В качестве основных рассматриваются экономические методы управления, выявление экономических параметров, воздействие (изменение) на которые и позволит достичь желаемого состояния системы в целом.
В работе при анализе функционирования производства сельскохозяйственных продуктов использованы статистические данные Конаковского и Максатихинского районов. Главы администраций этих районов на основании анализа развития сельского хозяйства за последние пять лет отмечают, что, хотя за последние годы темпы спада производства продуктов АПК несколько снижаются, сельское хозяйство Тверской области продолжает деградировать. В качестве основных причин кризиса сельского хозяйства отмечаются:
Непоследовательность политики государства в области сельского хозяйства. Неоднократные попытки административного решения проблем без должного обоснования и обеспечения.
Диспаритет цен между различными сферами экономики далеко не в пользу сельского хозяйства. Цены на необходимые для сельского хозяйства товары промышленного производства (ГСМ, корма, удобрения, электроэнергию) за последние годы существенно повысились, а цены на основные виды сельхозпродукции (молоко, мясо) увеличились незначительно.
Отсутствие научно-обоснованного подхода к перспективам развития сельского хозяйства с учетом конкретных климатических условий.
Значительные потери сельхозпредприятий при хранении продуктов в непригодных для этого хранилищах или в случае продажи продукции по заведомо заниженным ценам.
Несовершенность системы кредитования сельхозпредприятий. Необоснованно высокие процентные ставки при предоставлении краткосрочных кредитов.
Отсутствие на селе достаточного количества квалифицированных кадров, способных к принятию ответственных решений в конкретных условиях реформирования экономики.
Среди вышеперечисленных причин кризисного состояния сельского хозяйства здесь отметим отсутствие научно-обоснованного подхода к перспективам развития сельского хозяйства, подмена обоснованных решений волюнтаризмом и администрированием. Эти обстоятельства подтверждают актуальность поставленной в работе задачи.
Структура агропромышленного комплекса представлена на рис. 1.1. Она довольно сложна. В данной работе рассматривается только подсистемаи производителей сельхозпродукции.
Это в определенном смысле первичный, исходный блок АПК. Производство продуктов дает основу, смысл функционирования АПК в целом. Как следует из дальнейшего содержания настоящей работы, математический системный подход к анализу подсистемы с/х производителей позволяет получить некоторые рекомендации по управлению этой подсистемой.
![]()
![]()
![]()
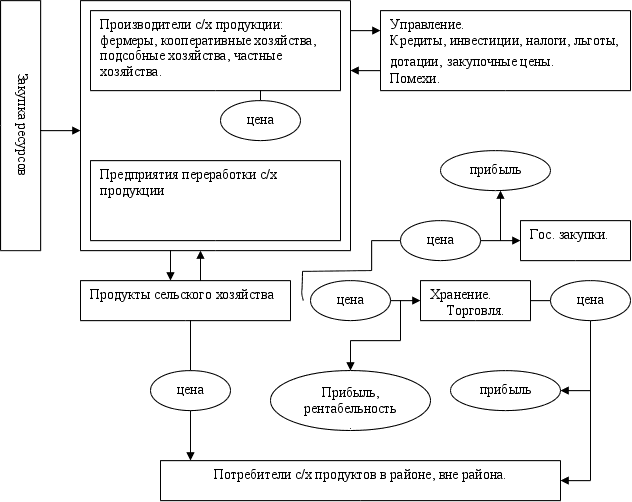
Рис. 1.1
3.Анализ производства продуктов в районных АПК.
Анализ производства продуктов проводится на примере функционирования агропромышленных комплексов Максатихинского и Конаковского районов за период с 1993 по 1996 год. Статистические данные взяты из [8], [8], [8].
Несмотря на некоторые различия в структуре хозяйства двух районов, основные тенденции развития сельского хозяйства идентичны. Производителями сельхозпродукции в районах являются:
относительно крупные предприятия, образованные на базе прежних совхозов и колхозов: 27 в Максатихинском районе и 11 в Конаковском, в дальнейшем вне зависимости от форм собственности будем называть их “сельхозпредприятиями”;
фермерские хозяйства;
подсобные хозяйства;
личные хозяйства.
Максатихинский район по структуре хозяйства типичен для Тверской области. В районе 27 сельхозпредприятий, в том числе 20 с коллективно-долевой формой собственности и 7 с коллективно-совместной собственностью.
Конаковский район имеет более развитую промышленность, а сельское хозяйство носит достаточно пестрый характер. Из 11 сельских предприятий два специализированные: госпредприятие (птицефабрика) “Красный Луч” и ТОО “Мелково” (зверосовхоз). В числе остальных предприятий два совхоза (госпредприятия), колхоз, коллективное сельхозпредприятие, имеющие специализированное производство куриного мяса и яиц, три АО и опытно-производственное предприятие.
Данные о производстве основных сельхозпродуктов во всех видах хозяйств Максатихинского и Конаковского районов в 1993-96гг. приведены в таблицах 2.1, 2.2, 2.3, 2.4.
Таблица 3.1 Производство зерна.
| 1993 г. | 1994 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| тонн | % | Тонн | % | тонн | % | тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 26373 | 97,3 | 11476 | 100 | 15674 | 94,8 | 13888 | 98,6 |
| Фермерские хозяйства | 460 | 1,7 | 0 | 0 | 456 | 2,8 | 82 | 0,5 |
| Подсобные хозяйства предприятий | 142 | 0,5 | 0 | 0 | 279 | 1,7 | 54 | 0,4 |
| Личные хозяйства | 132 | 0,5 | 0 | 0 | 129 | 0,7 | 67 | 0,5 |
| Всего по району | 27107 | 100 | 11476 | 100 | 16538 | 100 | 14091 | 100 |
| 1995 г. | 1996 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| тонн | % | Тонн | % | тонн | % | тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 11195 | 94,3 | 9984 | 98,4 | 12817 | 94,4 | 9516 | 98,2 |
| Фермерские хозяйства | 232 |
2,0 |
10 | 0,1 | 312 | 2,3 | 31 | 0,3 |
| Подсобные хозяйства предприятий | 142 | 1,2 | 11 | 12 | 170 | 1,3 | 97 | 1,0 |
| Личные хозяйства | 300 | 2,5 | 94,3 | 9984 | 278 | 2,0 | 44 | 0,5 |
| Всего по району | 11869 | 100 | 10151 | 100 | 13577 | 100 | 9668 | 100 |
Таблица 3.2 Производство молока 1993 - 1996гг.
| 1993 г. | 1994 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| Тонн | % | Тонн | % | Тонн | % | тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 13450 | 60,0 | 13350 | 74,0 | 11658 | 55,8 | 11387 | 69,0 |
| Фермерские хозяйства | 142 | 0,6 | 311 | 1,8 | 322 | 1,6 | 285 | 1,7 |
| Подсобные хозяйства предприятий | 82 | 0,4 | 116 | 0,6 | 60 | 0,3 | 127 | 0,8 |
| Личные хозяйства | 8744 | 39,0 | 4263 | 23,8 | 8830 | 42,3 | 4700 | 28,5 |
| Всего по району | 22418 | 100 | 18040 | 100 | 20874 | 100 | 16499 | 100 |
| 1995 г. | 1996 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| Тонн | % | Тонн | % | Тонн | % | Тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 9874 | 53,6 | 10749 | 66,8 | 9513 | 49,4 | 8708 | 62,0 |
| Фермерские хозяйства | 384 | 2,1 | 166 | 1,0 | 450 | 2,3 | 160 | 1,1 |
| Подсобные хозяйства предприятий | 25 | 0,1 | 185 | 1,2 | 25 | 0,1 | 171 | 1,2 |
| Личные хозяйства | 8137 |
44,2 |
4985 | 31,0 | 9270 | 48,2 | 4900 | 35,0 |
| Всего по району | 18420 | 100 | 16085 | 100 | 19258 | 100 | 13939 | 100 |
Таблица 3.3 Производство мяса.
| 1993 г. | 1994 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| Тонн | % | Тонн | % | Тонн | % | тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 2352 | 58,5 | 4830 | 74,0 | 1779 | 57,0 | 3968 | 74,9 |
| Фермерские хозяйства | 52 | 1,3 | 99 | 1,5 | 104 | 3,3 | 96 | 1,8 |
| Подсобные хозяйства предприятий | 68 | 1,7 | 231 | 3,5 | 63 | 2,0 | 223 | 4,2 |
| Личные хозяйства | 1549 | 38,6 | 1370 | 21,0 | 1175 | 37,7 |
1016 |
19,1 |
| Всего по району | 4021 | 100 | 6530 | 100 | 3121 | 100 | 5303 | 100 |
| 1995 г. | 1996 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| Тонн | % | Тонн | % | Тонн | % | Тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 1067 | 50,7 | 3860 | 77,4 | 962 | 48,1 | 3267 | 75,2 |
| Фермерские хозяйства | 31 | 1,5 | 15 | 0,3 | 32 | 1,6 | 15 | 0,3 |
| Подсобные хозяйства предприятий | 16 | 0,8 | 208 | 4,2 | 106 | 5,3 | 159 | 3,7 |
| Личные хозяйства | 990 | 47,0 | 901 | 18,1 | 900 | 45,0 | 900 | 20,8 |
| Всего по району | 2104 | 100 | 4984 | 100 | 2000 | 100 | 4342 | 100 |
Таблица 3.4 Производство картофеля.
| 1993 г. | 1994 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| Тонн | % | Тонн | % | Тонн | % | тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 2335 | 20,8 | 12558 | 41,3 | 736 | 8,3 | 9925 | 36.1 |
| Фермерские хозяйства | 89 | 0,8 | 672 | 2,2 | 46 | 0,5 | 533 |
1,9 |
| Подсобные хозяйства предприятий | 143 | 1,3 | 393 | 1,2 | 65 | 0,7 | 304 | 1,1 |
| Личные хозяйства | 87251 | 77,1 | 16805 | 55,3 | 8053 | 90,5 | 16670 | 60,9 |
| Всего по району | 11312 | 100 | 30368 | 100 | 8900 | 100 | 27352 | 100 |
| 1995 г. | 1996 г. | |||||||
| Максатиха | Конаково | Максатиха | Конаково | |||||
| Тонн | % | Тонн | % | Тонн | % | Тонн | % | |
| Хозяйства с коллективно-долевой собственностью | 563 | 2,6 | 7871 | 19,6 | 555 | 2,3 | 6199 | 22,6 |
| Фермерские хозяйства | 214 | 1,0 | 502 | 1,2 | 114 | 0,5 | 136 | 0,5 |
| Подсобные хозяйства предприятий | 0 | 0 | 257 | 0,6 | 0 | 0 | 219 | 0,8 |
| Личные хозяйства | 20667 | 96,4 | 31494 | 78,6 |
23316 |
97,2 | 20843 | 76,1 |
| Всего по району | 21444 | 100 | 40124 | 100 | 23985 | 100 | 27396 | 100 |
Из приведенных данных следует, что общее количество произведенной сельхозпродукции с каждым годом уменьшается, хотя темп снижения несколько замедляется. Наиболее резко уменьшается производство продуктов в сельхозпредприятиях. Как следует из данных таблиц, в Максатихинском районе производство в 1996г. в процентах от 1993г. составляет: зерна — 48,6%, молока — 70,1%, мяса — 23,8%, картофеля — 24,8%. Соответственно в Конаковском районе зерна — 82,9%, молока — 65,2%, мяса — 67.6%, картофеля — 49,4%.
Сельхозпредприятия остаются основными производителями зерна, для остальных видов продукции доля сельхозпредприятий с каждым годом падает. Для Конаковского района эта тенденция характерна в несколько меньшей степени, в основном, благодаря сохранившимся госпредприятиям. Систематически увеличивается себестоимость производимой продукции, причем темпы увеличения цены реализации продуктов отстают от темпов увеличения себестоимости. Соответствующие данные, пересчитанные в цены 1993 года, приведены в таблице 2.5.
Таблица 3.5 Рост себестоимости и цены реализации в % 1996г. по отношению к 1993г в сопоставимых ценах
| Максатихинский район | Завидовский район | |||
| Себестоимость |
Цена реализации |
Себестоимость | Цена реализации | |
| Зерно | 344 | 108 | 142 | 141 |
| Молоко | 213 | 131 | 191 | 147 |
| Мясо | 234 | 360 | 295 | 96 |
| Картофель | - | - | 241 | 128 |
Причины такого положения известны. Ухудшение финансового положения предприятий привело к сокращению применения удобрений, работ по защите растений от вредителей и болезней, работ по семеноводству и племенному животноводству. Заметно ухудшилось плодородие почв.
Вклад фермерских хозяйств в производство продуктов не значителен. Доля производства продуктов фермерских хозяйств в обоих районах находится в пределах 0,3-2,3%.
Фермерские хозяйства Тверской области в основном мелкотоварные. Так в Конаковском районе средний размер площади фермерских хозяйств 14,6 га с числом работающих 2-3 человека. Из 128 хозяйств 93 не имеют скота, во всех фермерских хозяйствах только 70 коров. Мелкотоварные фермерские хозяйства не имеют перспективы. И дело здесь не в отсутствии должного финансирования и технического оснащения. Мелкотоварное фермерское хозяйство характеризуется низкой производительностью и неконкурентоспособно. Чтобы выжить мелкий фермер нуждается в кооперации в части получения различных услуг, обработки и сбыта продуктов, закупки семян и горючего, ремонта техники, эксплуатации оборудования разного назначения и пр.
Подсобные хозяйства предприятий ориентированы на частичное обеспечение столовых ( и работников) промышленных предприятий. Как видно из таблиц 2.1, 2.2, 2.3 и 2.4 их вклад в производство продуктов незначителен.
Личные хозяйства (ЛХ) созданы для удовлетворения потребностей крестьянских семей, но большинство ЛХ производят продукты и для продажи. Доля ЛХ в производстве продуктов ежегодно увеличивалась и достигла в 1996г. (в % от общего районного производства) в производстве картофеля — 97,2 % и 76,1% ( здесь и далее 1-я цифра относится к Максатихе, 2-я — к Конаково), в производстве молока — 48,2% и 35,0%, мяса — 45.0% и 20,8%, зерна — 2,0 % и 0,5%. Подавляющим является доля ЛХ в производстве овощей открытых грунтов.
Динамика роста доли ЛХ видна из таблиц 2.1, 2.2, 2.3 и 2.4. Производственные показатели в ЛХ выше, чем в сельхозпредприятиях. Сравнительные данные средних по районам значений надоев молока и урожайности картофеля приведены в таблицах 2.6 и 2.7.
Таблица 3.6 Надои молока на 1 корову , (кг)
| 1994г. | 1995г. | 1996г. | ||||
| Макса-тиха | Конаково | Макса-тиха | Конаково | Макса-тиха | Конаково | |
| Хоз-ва с коллект. Формой собственности | 1830 | 2080 | 1630 | 2050 | 1730 | 1850 |
|
Личные подсо Бные хозяйства |
3340 | 3240 | 3450 | 3200 | 3940 | 3280 |
Таблица 3.7Урожайность картофеля, (ц/га)
| 1994г. | 1995г. | 1996г. | ||||
| Макса-тиха | Конаково | Макса-тиха | Конаково | Макса-тиха | Конаково | |
| Хоз-ва с коллект. Формой собственности | 72,5 | 97 | 71,1 | 117 | 102,5 | 95 |
| Личные подсобные хозяйства | 115 | 160 | 129 | 201 | 146 | 135 |
Себестоимость производства в ЛХ оценить трудно. Причиной этого является отсутствие статистических данных по затратам труда в ЛХ, а также по объему “помощи” (поддержки), которую фактически получают ЛХ от сельхозпредприятий.
Особенностью ЛХ является то, что они являются как бы надомными работниками для сельхозпредприятий, но не связаны с ними никакими формальными договорными отношениями. Поэтому мелкотоварные личные подсобные хозяйства оказались экономически выгодными для их владельцев. Возможная поддержка ЛХ сельхозкооперативами заключается в приобретении удобрений, обеспечении определенного вида работ механизмами и горючим, содержании на выпасах личного скота вместе с общественным. Сельхозпредприятия могут также скупать продукты в ЛХ и организовывать их продажу.
Существует мнение, что ЛХ процветают главным образом там, где сельхозпредприятия являются экономически слабыми. Но это не так. Именно экономически крепкие сельскохозяйственные предприятия располагают большими возможностями по поддержке ЛХ. Разорение сельхозпредпрития однозначно влечет и упадок производства в ЛХ, что в конечном счете приведет к дальнейшему, возможно обвальному, падению производства сельхозпродуктов. Однако труженики сельского хозяйства далеко не всегда это понимают, и порой идет просто растаскивание коллективной собственности, что особенно показательно для предприятий с коллективно-долевой формой собственности. По-видимому, преобладанием предприятий с таким видом собственности в Максатихинском районе и объясняется относительно меньшая, чем в Конаковском районе, их доля в производстве продуктов (табл. 2.2, 2.3 и 2.4).
Таким образом, хотя формально в составе АПК четыре подсистемы: сельхозкооперативы с различными формами собственности, личные хозяйства работников кооперативов, подсобные хозяйства промышленных предприятий и фермерские хозяйства, реально основной вклад в производство продукции осуществляют первые две подсистемы.
Между этими подсистемами существует определенное разделение труда. В ЛХ производится значительная доля продукции тех отраслей сельского хозяйства, которые сегодня мало механизированы. В ЛХ более тщательная обработка земли, своевременное внесение удобрений, лучший уход за скотом, хорошая сохранность урожая и пр.
Соответственно является актуальным анализ текущего состояния взаимодействующих подсистем, перспектив их развития.
В настоящее время крайне опасно нарушать стихийно сложившееся динамическое равновесие между СХП и ЛХ. Более того необходимо придать поддержке ЛХ со стороны сельхозпредприятий правовую основу. Форма и характер этой поддержки не должны зависеть от прихотей руководителей сельхозпредприятий. Труженики СХП должны быть уверены в получении поддержки их личных подсобных хозяйств, причем объем этой поддержки должен быть пропорционален вкладу труженика в работу сельхозпредприятия. Не следует вмешиваться в договорные отношения СХП и ЛХ и государственным органам, последние должны только оказывать помощь в укреплении правовых основ таких отношений.
Необходимо разработать математические модели для оценки возможных экономических методов воздействия на производство ЛХ и обеспечение расширенного воспроизводства в СХП.
Сложившаяся под давлением определенных обстоятельств структура сельского хозяйства является далеко не идеальной, скорее “вынужденной”. Даже при поддержке со стороны СХП мелкотоварные ЛХ длительной перспективы в массовом производстве основных продуктов сельского хозяйства не имеют. Трансформация структуры сельского хозяйства должна идти по направлению укрепления относительно крупных сельских хозяйств. Для каждой климатической зоны оптимальный размер такого хозяйства различен. Перспективные крупные сельские хозяйства могут быть, либо акционерными хозяйствами, либо крупными фермерскими хозяйствами с наемным трудом.
Следует заметить, что по мере укрепления экономики и совершенствования технологии в крупных хозяйствах окажется, что производство целого ряда продуктов в ЛХ экономически менее выгодно, и труженики сельского хозяйства будут более заинтересованы в результатах своей работы в сельхозпредприятиях. В таком случае будет увеличиваться доля крупных конкурентоспособных хозяйств в производстве всех основных сельскохозяйственных продуктов. При этом ЛХ, как подсобные хозяйства кооперативов будут естественно перепрофилироваться на такие виды продукции, где ручной труд останется экономически более эффективным.
Трансформация структуры сельского хозяйства, в направлении развития рентабельных конкурентоспособных хозяйств возможна при усилении роли государства в регулировании процессов, происходящих на селе, но не путем возврата к волюнтаристским решениям, административно-командным методам, а с помощью экономических методов.
Таким образом, можно отметить, что при сохранении существующего положения вещей перспектива развития этого сектора экономики будет следующей.
Некоторые виды продукции, такие как мясо, картофель, молоко и пр. коллективным хозяйствам производить становится невыгодно, ввиду того, что цены на них занижены «частниками». Глядя на статистику по районам, можно заявить, что положение дел именно таково.
Так как ранее вышеперечисленные продукты составляли довольно большой процент конечного продукта предприятий АПК, сейчас они несут ни с чем не сопоставимые убытки.
Отсутствие прибылей приведет в конце концов к тому, что коллективные хозяйства обанкротятся и «пойдут с молотка». В результате ЛХ не смогут получить достаточную материальную поддержку и вынуждены будут поднять цены на свою продукцию из-за неизбежного увеличения затрат на производство.
Это повлечет нарушение баланса цен между импортными и отечественными товарами, что стимулирует заполонение рынка зарубежными продуктами и неизбежный скачок инфляции (см. [8]).
4.Использование преобразования Лапласа для моделирования экономических процессов
Для синтеза модели используем математический аппарат, сущность которого представлена ниже. Показано, что это позволяет вполне адекватно моделировать деятельность и развитие большинства экономических (и не только) систем.
Если функционирование какой-либо системы может быть описано в виде линейного дифференциального или интегрального уравнения, например:
![]() ,
m
,
m
где x(t) – функция входного, экзогенного воздействия на систему,
y(t) – функция выходного процесса или реакция системы на внешнее воздействие, тогда для дальнейшего изучения и анализа имеет смысл воспользоваться трансформацией данного уравнения с помощью преобразования Лапласа ввиду его замечательных свойств перевода дифференциальных и интегральных выражений в алгебраические.
Смысл преобразования Лапласа заключается в том, что оно переводит функцию времени f(t) в функцию частот F(s). Математически это записывается следующим образом:
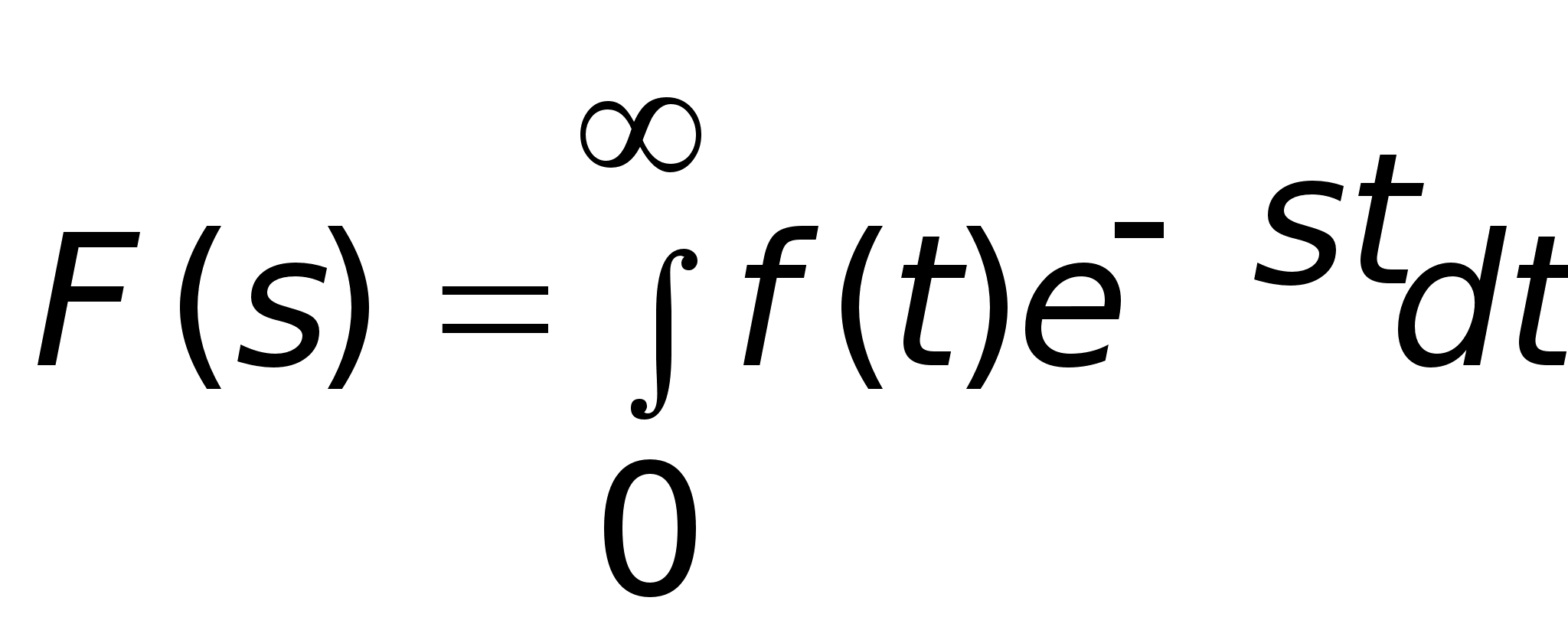
и наоборот
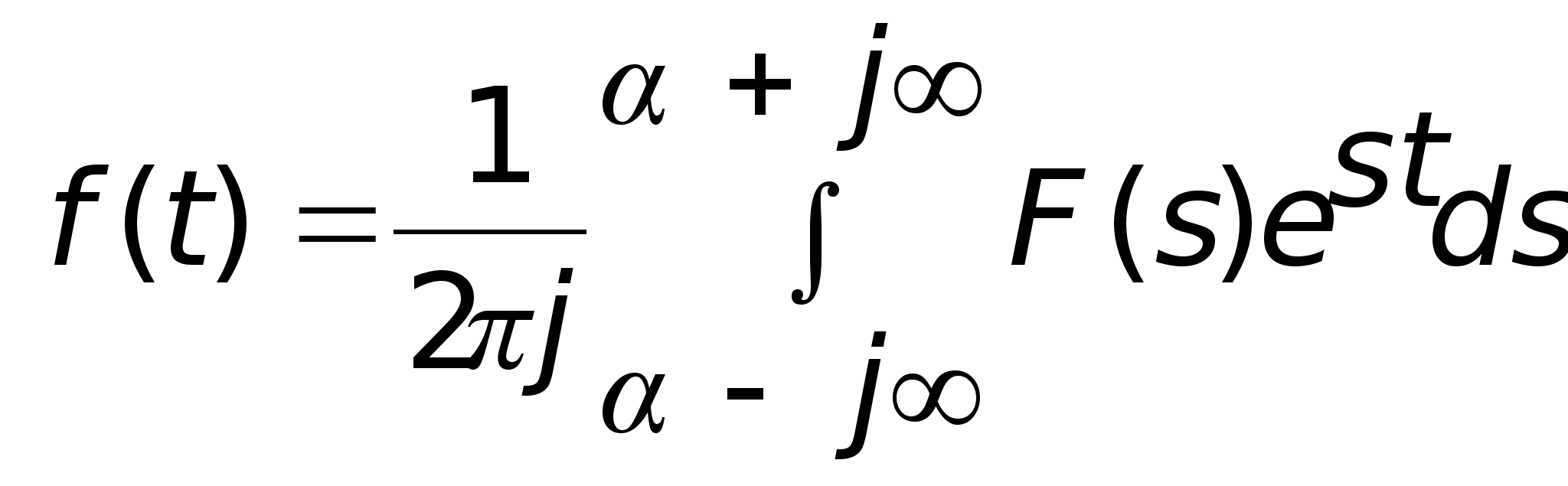 ,
,
где функцию f(t) называют оригиналом, а функцию F(s) – изображением.
Передаточная функция любой линейной системы может быть дизагрегирована на отдельные составляющие – звенья. Таким образом, каждому определенному экономическому процессу может быть сопоставлено звено определенного типа.
4.1.Пропорциональное (усилительное) звено
Примерами для моделирования в форме пропорциональных звеньев могут быть такие функции в хозяйственной деятельности, как переходы от оптовых цен на продукцию к розничным ценам, от потребностей в материалах в натуральном выражении к потребностям в денежном выражении и т. д. Формулы оригинала и изображения имеют вид
![]() .
.
В этом случае передаточной функцией звена будет следующее соотношение:
![]() ,
,
где к – коэффициент усиления
4.2.Дифференцирующее и интегрирующее (накопительнное) звенья
Примером деятельности для моделирования в форме дифференцирующего звена может служить накопительный учет объема продаж в торговле, на основании которого выдается информация о текущей продаже за малые промежутки времени. Интегрирующим звеном может быть смоделировано, например, накопление производственных фондов в производственном процессе.
Оригинал и изображение уравнения дифференцирующего звена имеют вид
![]() ,
,
интегрирующего звена
![]() .
.
Тогда передаточные функции:
![]() –
дифферецирующего
звена,
–
дифферецирующего
звена,
![]() –
интегрирующего
звена.
–
интегрирующего
звена.
4.3.Звенья запаздывания
Запаздывание реакции на внешние воздействия принципиально существует во всех объектах экономики, например, выпуск продукции по отношению к поступлению материалов в производство, ввод производственных фондов по отношению к выделению на них капиталовложений, принятие решений о заказах на товары в ответ на выявленный спрос и т. д. Для моделирования таких явлений в динамических системах часто применяют звенья дискретного запаздывания и инерционные звенья.
Звено дискретного запаздывания описывается формулой:
![]() .
.
В этом случае графически оба процесса имеют одинаковый вид. Однако выходной процесс смещен на T единиц по оси времени вправо. Величина T называется лагом.
Инерционными звеньями называют такие, у которых реакция на входное воздействие запаздывает и форма выходного процесса не повторяет форму входного процесса как при дискретном запаздывании. Если входной процесс представляет собой поток материалов, энергии, денежных средств и т. д., то внутри звена накапливается определенное количество этих материально-вещественных элементов, равное разности входного и выходного процессов. Инерционными звеньями моделируют также реакцию покупателей в ответ на поступление товара в продажу, ввод основных производственных фондов, в ответ на капиталовложения и т. д.
Инерционное звено первого порядка описывается уравнением следующего вида:
![]() .
.
Отсюда изображение процесса на выходе звена
![]() ,
,
где
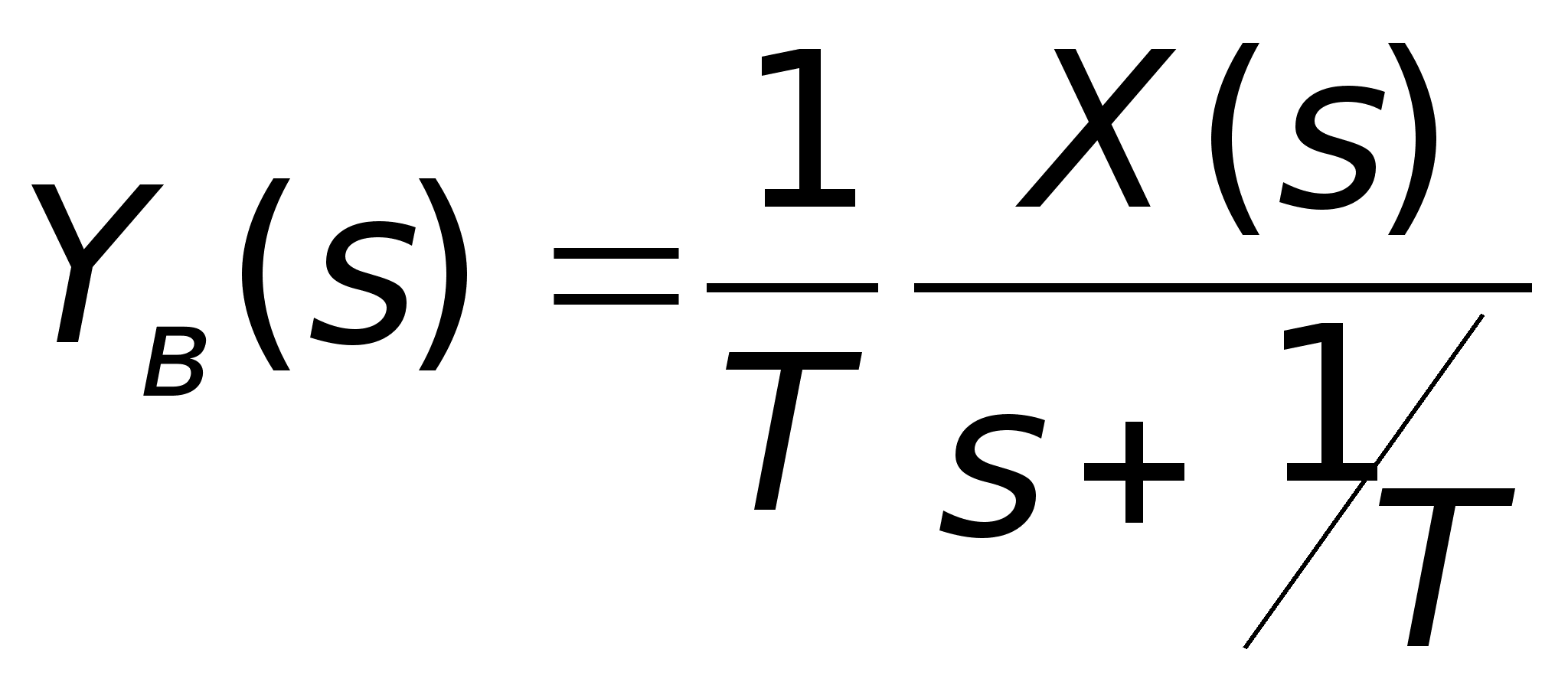 ,
,
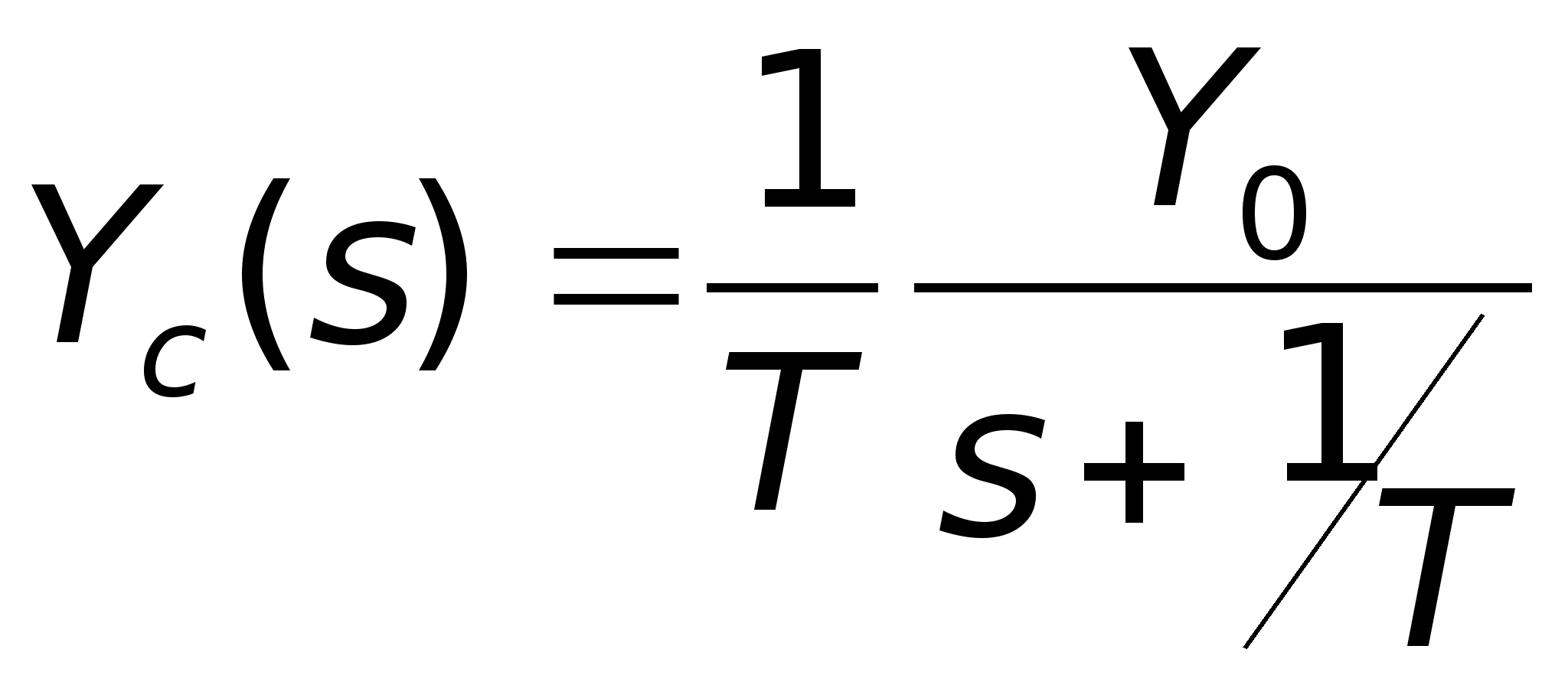 .
.
Следовательно, передаточная функция инерционного звена
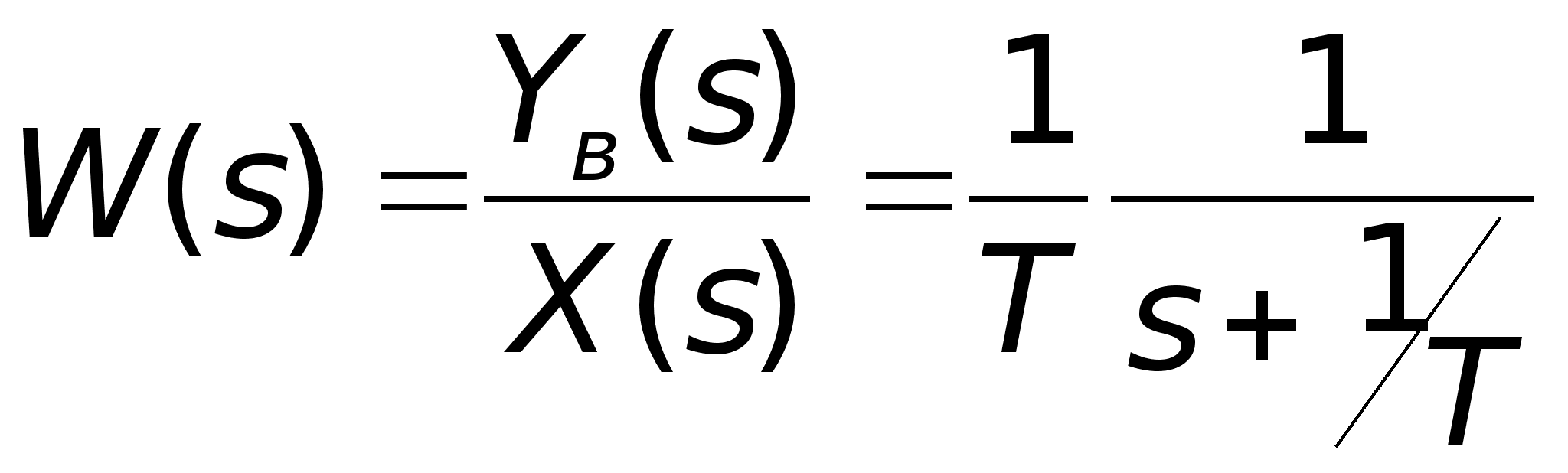 .
.
Оригинал
этого уравнения
представляет
собой реакцию
на импульс в
виде дельта-функции
![]() .
Оригинал имеет
вид:
.
Оригинал имеет
вид:
![]()
Изображение и оригинал реакции на единичную ступенчатую функцию запишутся в виде:
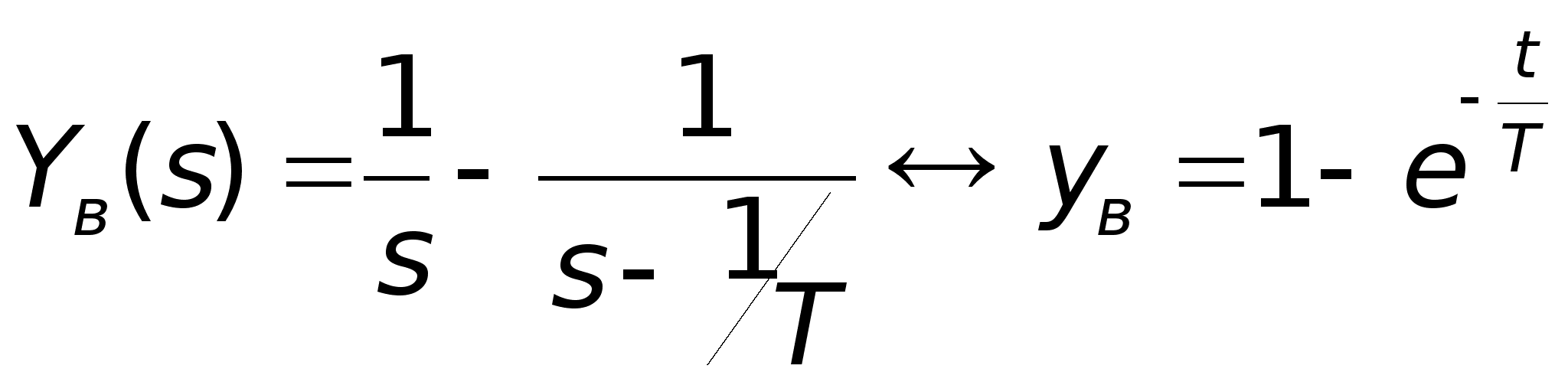 .
.
Своеобразие
экономических
объектов,
моделируемых
инерционными
звеньями, состоит
в том, что в них
накапливается
разность вещественных
единиц, из которых
состоят входной
и выходной
потоки. Обозначим
накопленное
количество
единиц через
![]() .
Тогда
.
Тогда
![]() ,
,
где z0=z(0) – количество накопленных единиц в нулевой момент времени. Таким образом, при любом экзогенном воздействии и начальном состоянии звена z0 интенсивность (скорость, темп) выходного процесса инерционного звена пропорциональна текущему количеству накопленных единиц внутри звена. Коэффициент пропорциональности равен 1/T. Очевидно, что статистическое постоянство этого коэффициента в любых объектах экономики может служить признаком того, что динамической моделью объекта является инерционное звено.
5.Динамическая модель.
В этой главе будет рассмотрено взаимодействие интересующих нас субъектов в динамике с использованием математического аппарата преобразования Лапласа. Будут выведены ограничения на выделение помощи частным хозяйствам, при которых кооперативы не будут деградировать. Это пригодится нам в дальнейшем при синтезе математической модели, включающей в себя регламентирование отчислений в зависимости от распределения трудовых ресурсов.
5.1.Производственная функция и производственные фонды.
В процессе производства, с одной стороны, осуществляются капиталовложения и ввод производственных фондов в эксплуатацию. Этим процессом обусловлено увеличение количества производственных фондов. С другой стороны, происходит уменьшение производственных фондов в результате амортизации и выбытия. Если в качестве модели движения производственных фондов принять инерционное звено первого порядка, у котороко внешнее воздействие I(t) – интенсивность потока капиталовложений, S(t) – интенсивность потока амортизации и T – лаг эксплуатации производственных фондов, тогда текущая стоимость производственных фондов определяется операторным уравнением:
![]() , (1)
, (1)
где F0 – начальная стоимость производственных фондов.
Запишем изображение процесса амортизации в виде:
![]() , (2)
, (2)
то есть амортизация пропорциональна текущей стоимости производственных фондов и составляет постоянную ее долю. Доля амортизированных фондов n – норма амортизации. Подставив реакцию A(s) в (1) и решив выведенное уравнение относительно F(s), получим следующую зависимость накопленного количества производственных фондов от капиталовложений:
![]() . (3)
. (3)
Предположим теперь, что производственная функция зависит только от стоимости производственных фондов, то есть является однофакторной. В данном случае следует абстрагироваться от трудовых ресурсов и прочих параметров, так как они не влияют на окончательный результат. Запишем однофакторную динамическую производственную функцию сельхозпредприятия:
![]() , (4)
, (4)
где – фондоотдача.
Подставим в эту функцию полученное выражение для производственыых фондов и получим зависимость интенсивности выпуска от интенсивности потока капиталовложений в операторной форме:
![]() ,
,
![]() , (5)
, (5)
где (s) – передаточная функция производственного звена.
5.2.Модель развития отдельного предприятия.
В синтезе модели отдельного предприятия будем исходить из того, что объем произведенной и реализованной продукции зависит от остаточной стоимости ОПФ, которая может увеличиваться или уменьшаться. Она возрастает в зависимости от капиталовложений и уменьшается в результате амортизации и выбытия некоторой части основных средств. Следовательно, рост объемов выпуска может быть обеспечен в том случае, если капиталовложения превышают количество изношенных ОПФ, тогда и текущая их стоимость увеличивается. При снижении стоимости ОПФ рост объема выпуска может быть достигнут за счет повышения фондоотдачи, то есть влияния научно-технического прогресса. Эти явления отражает модель производства в виде однофакторной динамической производственной функции.
Капиталовложения слагаются из централизованных средств I(t) и отчислений от дохода U(t). Предположим, что отчисления регламентируются нормативом a
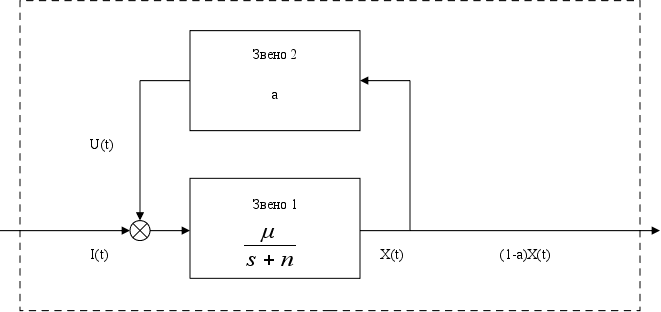
Чтобы найти передаточную функцию системы необходимо разрешить систему уравнений относительно X(s):
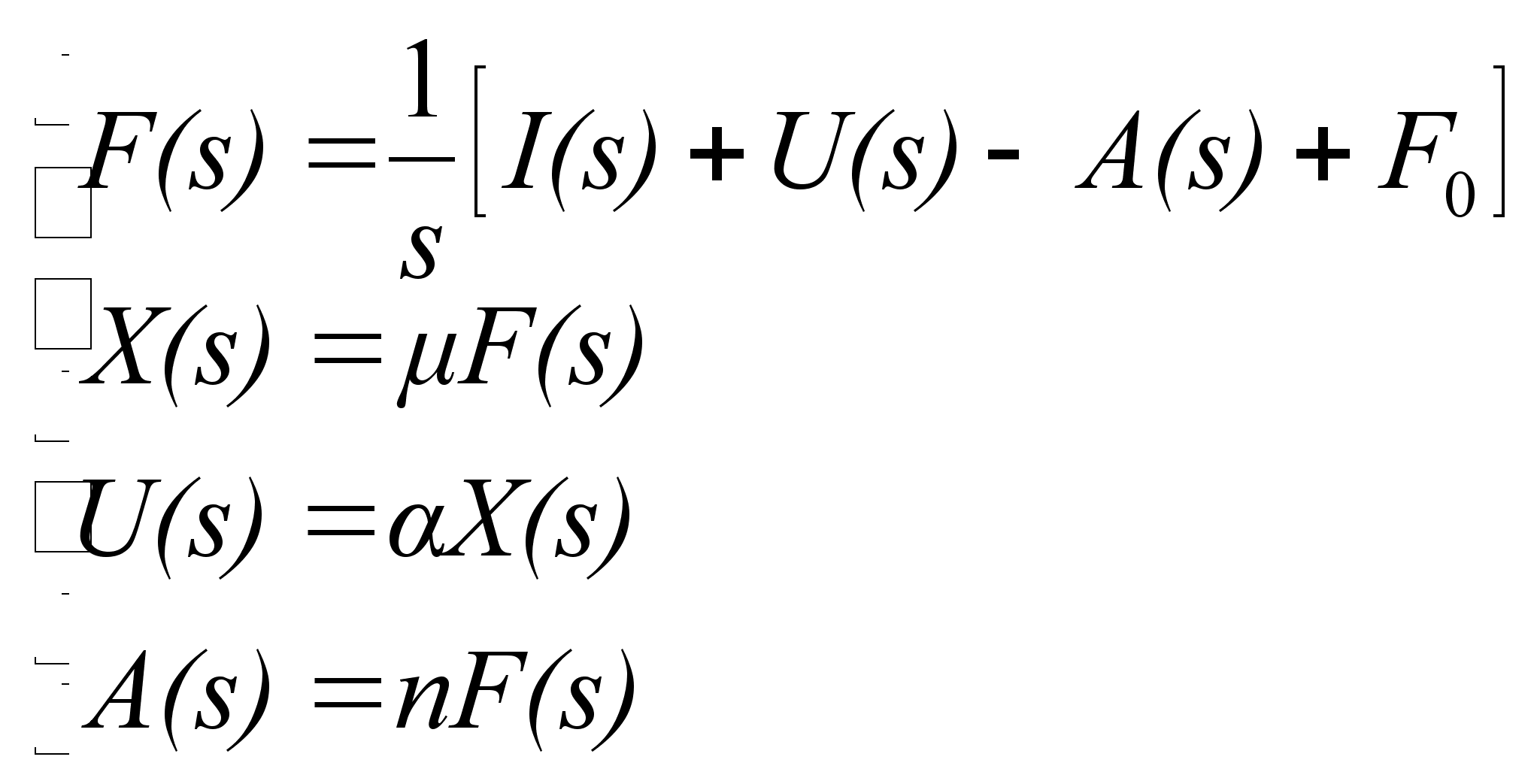 (6)
(6)
Где n – норма амортизации,
F0 – начальное значение стоимости ОПФ,
– фондоотдача в единицах измерения остаточной стоимости ОПФ,
a – норматив отчислений в фонд развития производства,
n – норма амортизации
Рис. 5.1
В результате получим:
![]() , (7)
, (7)
где
первое слагаемое
– вынужденная,
а второе – свободная
составляющая;
x0 –
начальное
значени еинтенсивности
производства
и реализации
продукции.
Передаточная
функция системы
равна
![]() . (8)
. (8)
Структура системы с такой передаточной функцией показана на рис. 5.1.
5.3.Динамика взаимодействия производства сельхозкооперативов и личных хозяйств членов этих кооперативов.
Рассмотрим теперь, как ведет себя передаточная функция применительно к нашей проблеме. Для этого необходимо предсталять себе структуру взаимосвязей и элементов системы. Искомая схема приводится нна рис. 5.2.


![]()
PI
Производство 2
Производство 1
ОПФ2
PX2
PY2
PX1
PY1
A2
U2
a2X2
(1-)a2X2
a2X2
I
I
П2+L2
П1+L1
A1
U1
I
X2
Y2
C2
X1
Y1
C1
Р
ОПФ1
a1X1
ис. 5.2.Где
| I | Внешние инветиции. |
|
I |
Инвестиции, направленные в коллективные хозяйства. (0 |
|
I |
Инвестиции, направленные в частные хозяйства. (0+=1) |
| X | Валовой продукт. |
| Y | Валовой продукт минус амортизационные отчисления. |
| C | Конечный продукт. |
| П | Природные ресурсы. |
| L | Трудовые ресурсы. |
| A | Амортизационные отчисления. |
| U | Чистые инвестиции (Расширенное воспроизводство). |
|
|
Доля валового продукта, идущая на капиталовложения. |
|
(1-)a2X2 |
Доля валового продукта коллективных хозяйств, идущая на инвестиции в частные хозяйства. |
Дополним
модель еще
одним условием.
Предположим,
что внешние
инвестиции
зависят от
эффективности
функционирования
сельхозкооператива
и примем
![]() ,
>0.
,
>0.
Как уже было сказано выше, производственный процесс описывается следующим уравнением:
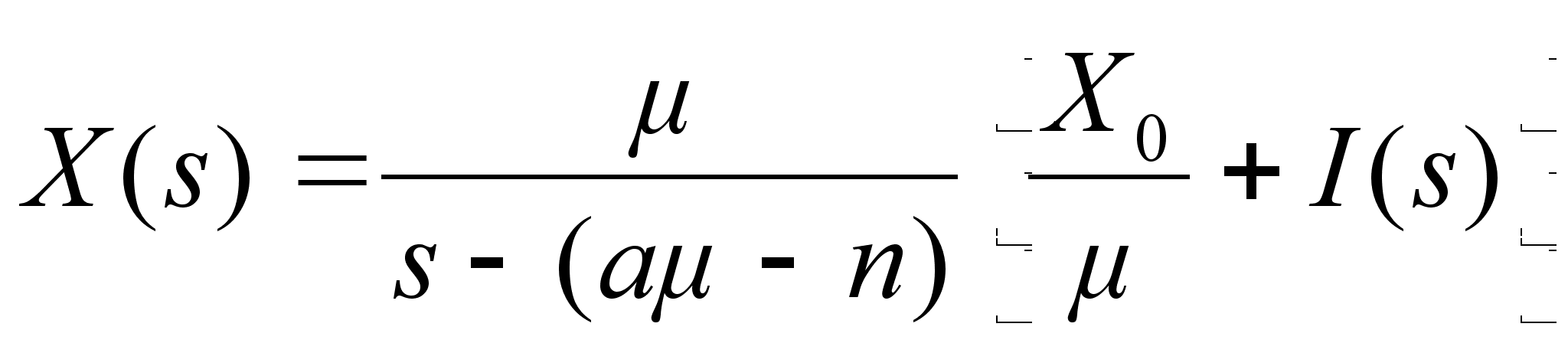 (9)
(9)
или с учетом нешего предположения:
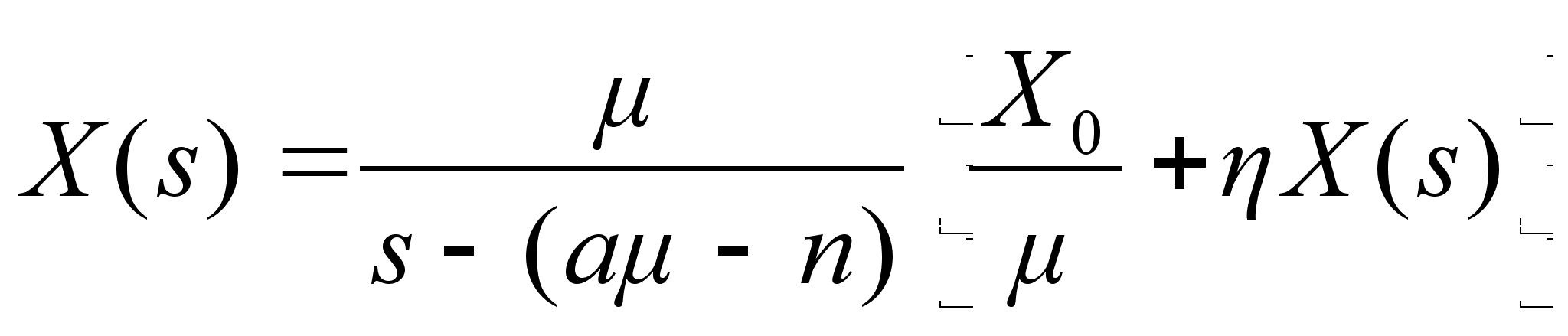 . (10)
. (10)
Тогда модель примет следющий вид:
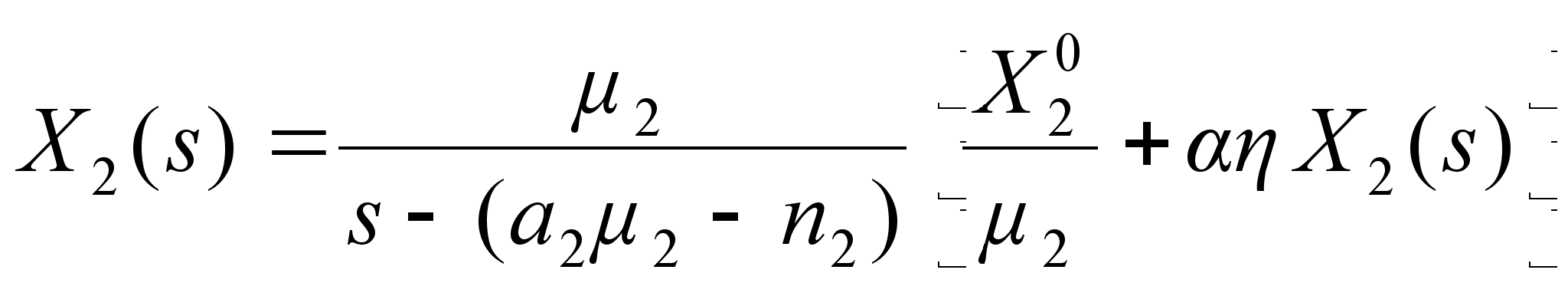 (11)
(11)
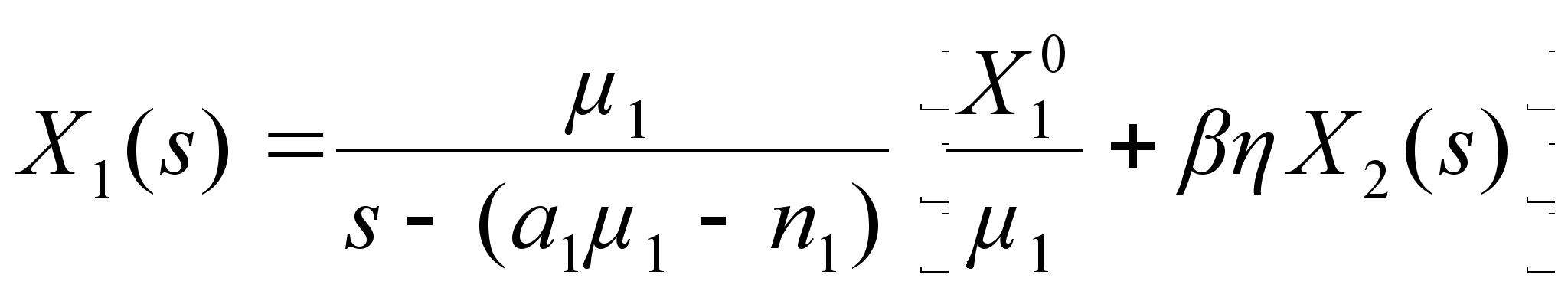 . (12)
. (12)
Из первого уравнения получим, что конечный продукт сельхозкооператива выразится следующим образом:
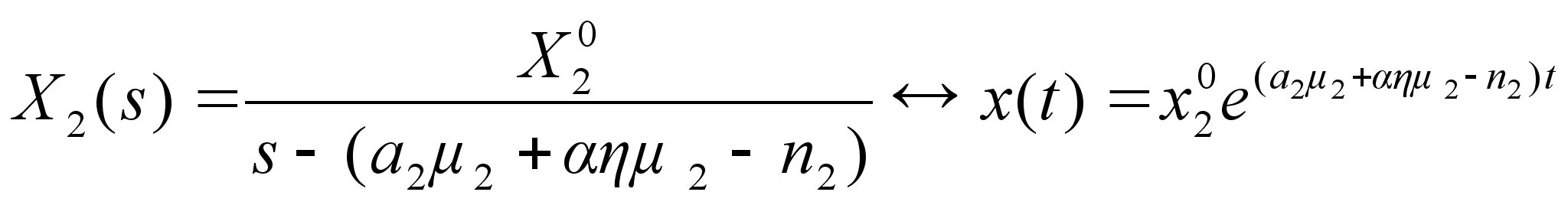 (13)
(13)
Отсюда условие безразличного равновесия:
![]() . (14)
. (14)
Для того, чтобы производство в сельхозкооперативе не деградировало, необходимо, чтобы:
![]() , (15)
, (15)
![]() . (16)
. (16)
Условие (16) можно трактовать как условие полного расхищения производственных фондов сельхозпредприятий.
Из (12) следует, что валовой продукт частных хозяйств будет:
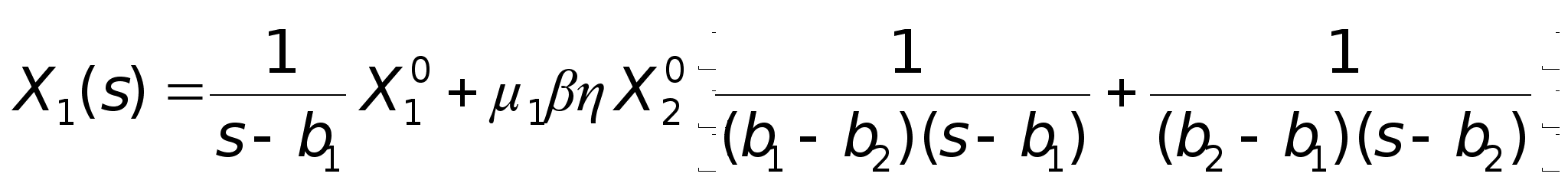 . (17)
. (17)
Где
![]() ,
,
![]() .
.
Отсюда
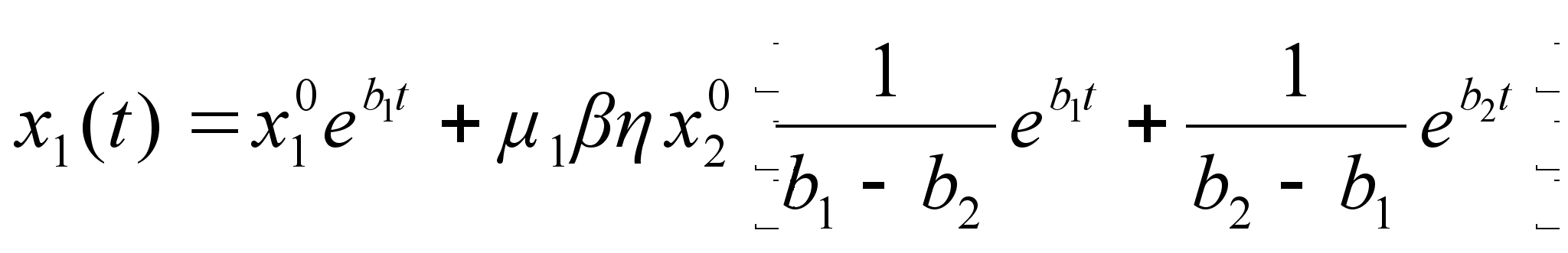 . (18)
. (18)
При отсутствии
внешних инвестиций
(I(t)=0)
часть валовых
капиталовложений
сельхозкооперативов
будет отвлекаться
на инвестиции
в производство
частных хозяйств.
Заметим, что
эта ситуация
более характерна
для сложившейся
экономической
ситуации, потому
что на данный
момент инвестиций
в агропромышленный
комплекс как
таковых нет.
Предположим,
что коллективное
производство
получит капиталовложений
![]() ,
а для частных
хозяйств некоторым
эквивалентом
внешних инвестиций
явится
,
а для частных
хозяйств некоторым
эквивалентом
внешних инвестиций
явится
![]() ,
где 0
,
где 0
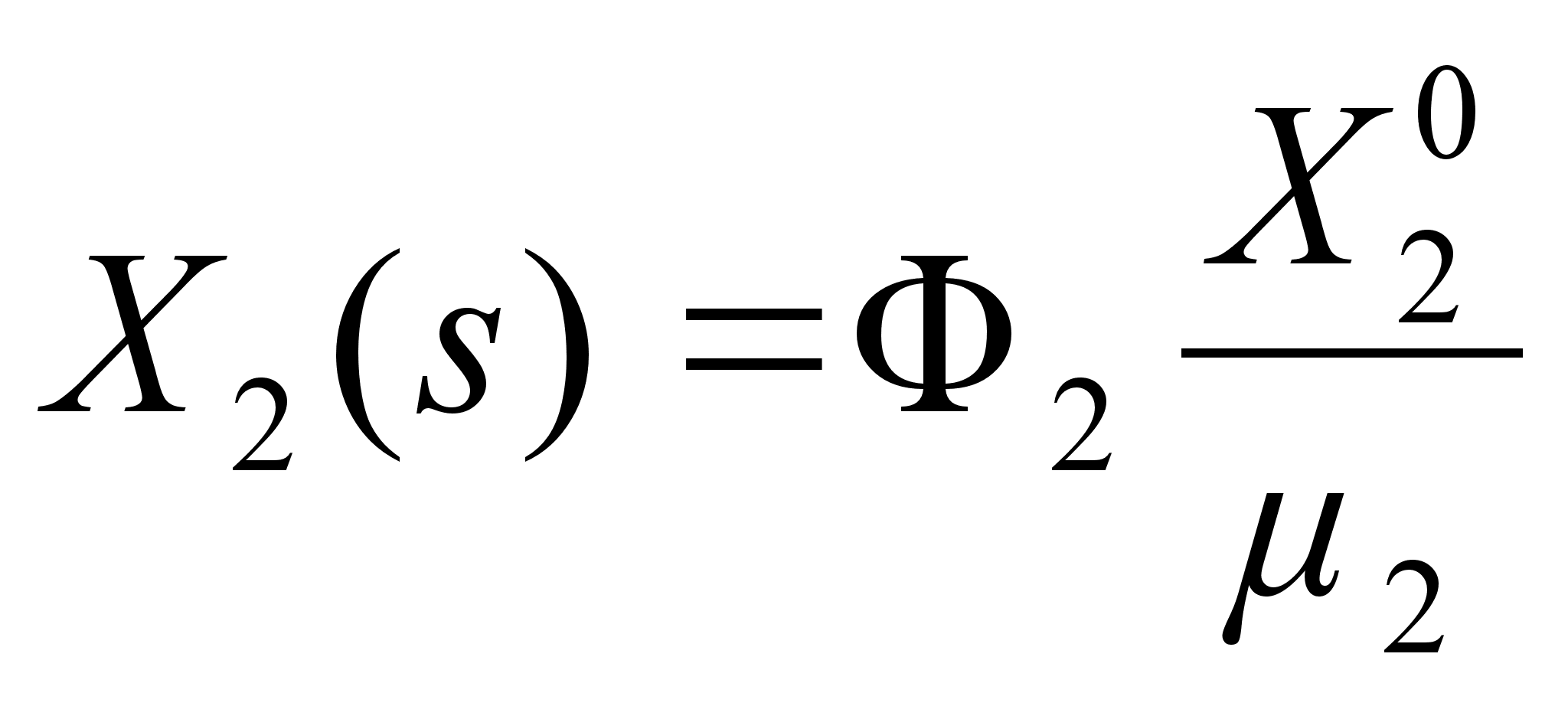 ,
,
![]() ; (19)
; (19)
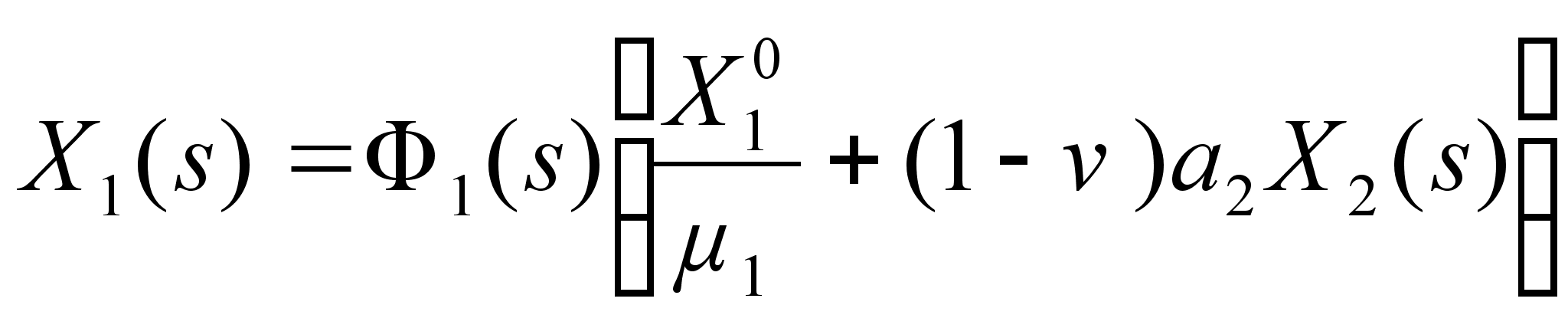 ,
,
![]() . (20)
. (20)
Условие
безразличного
равновесия
запишется в
виде:
![]() . (21)
. (21)
Расширенное
воспроизводство
в коллективном
хозяйстве будет
иметь место
при
![]() . (22)
. (22)
Из (19) и (20) следует:
![]() , (23)
, (23)
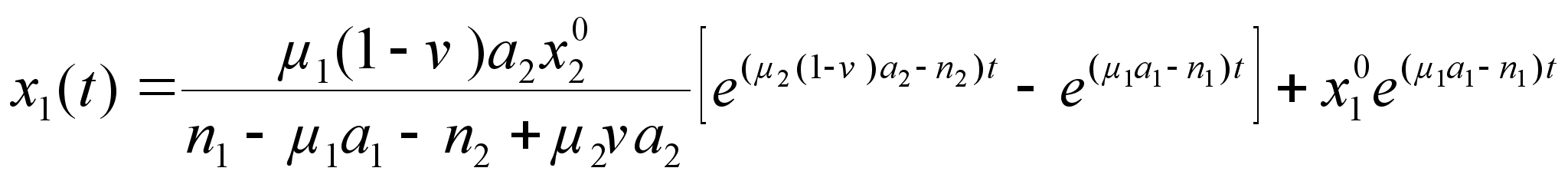 . (24)
. (24)
Таким
образом, исходя
из (22) необходимо
обеспечить
определенное
соотношение
экономических
коэффициентов
,
,
n,
a,
при котором
производство
в сельхозкооперативе
не деградирует
(![]() ),
а, что еще лучше,
прогрессирует
и увеличивает
объемы выпуска
продукции и
валовые капиталовложения
(
),
а, что еще лучше,
прогрессирует
и увеличивает
объемы выпуска
продукции и
валовые капиталовложения
(![]() ).
).
6.Модель взаимодействия хозяйств сельхозкооперативов и личных хозяйств членов кооперативов.
6.1.Структурная схема
В разделе 5 были получены условия обеспечения расширенного воспроизводства при совместном функционировании сельхозпредприятий и личных хозяйств работников этих предприятий. Рассмотрим далее, каким образом можно повысить эффективность этого взаимодействия.
Далее проанализирована модель, в которой личные хозяйства максимизируют свою прибыль за счет перераспределения доли труда, вложенного в предприятия и в личные хозяйства и эта доля зависит от коэффициента k, характеризующий поощрение личных хозяйств за труд, вложенный в сельхозпредприятие. Руководитель предприятия, зная подход личных хозяйств к распределению труда оптимизирует прибыль сельхозпредприятия за счет выбора значения коэффициента поощрения.
Как следует из приведенного анализа производства сельхозкооперативов в районных АПК Тверской области, вклад в производство фермерских и подсобных хозяйств незначителен. Соответственно, структура рассматриваемой системы производителей сельхозпродукции может быть представлена в виде двух взаимодействующих подсистем сельхозпредприятий с различными формами собственности и личных хозяйств членов этих кооперативов (Рис. 6.1).
Р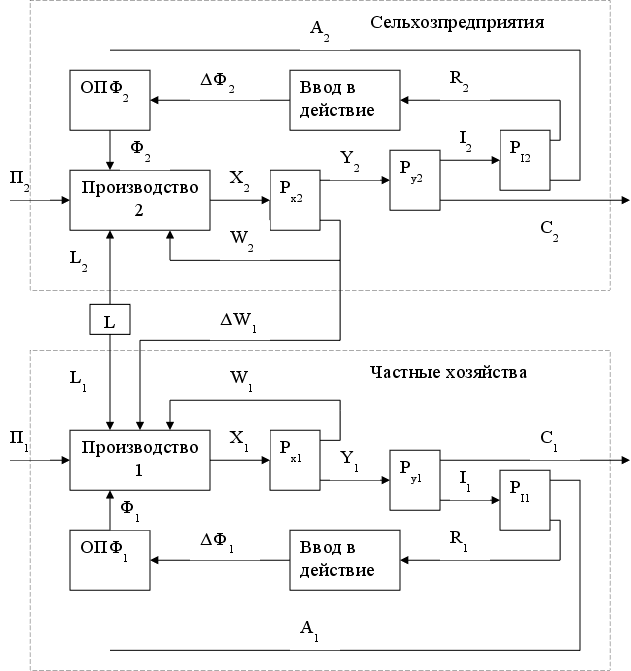
![]()
![]() ис.
6.1.
ис.
6.1.
| Где | |
| L | Труд, |
| П | Природные ресурсы, |
| Ф | Основные производственные фонды (ОПФ), |
| X | Валовой продукт, |
| W | Производственное потребление, |
| Y | Конечный продукт, |
| I | Валовые капитальные вложения, |
| C | Непроизводственное потребление, |
| А | Амортизационные отчисления, |
| R | Чистые капитальные вложения. |
Для данной схемы верны следующие соотношения:
Валовой продукт делится на производственное потребление и конечный продукт
![]() (1)
(1)
Аналогичным образом получим:
![]() (2)
(2)
![]() (3)
(3)
Объем наращивания ОПФ при расширенном воспроизводстве пропорционален «чистым» инвестициям:
![]() , (4)
, (4)
а амортизационные отчисления
![]() , (5)
, (5)
где – коэффициент амортизации оборудования. Тогда
![]() (6)
(6)
Однако (1) в случае коллективного хозяйства, при наличии «помощи» частным хозяйствам примет вид:
![]() , (7)
, (7)
где
![]() .
.
Таким
образом,
![]() делится
на производственное
потребление
коллективного
хозяйства и
«поддержку»
частных хозяйств.
Причем производственное
потребление
пропорционально
объему валового
продукта:
делится
на производственное
потребление
коллективного
хозяйства и
«поддержку»
частных хозяйств.
Причем производственное
потребление
пропорционально
объему валового
продукта:
![]() (8)
(8)
Основная идея регламентирования подобного вида «помощи» состоит в том, чтобы отток средств коллективного хозяйства был функцией трудового вклада работников в производство предприятия, т. е.
![]() . (9)
. (9)
Запишем теперь выражение для конечного продукта коллективного хозяйства с учетом проведенных рассуждений:
![]() (10)
(10)
или
![]() (11)
(11)
Предположим, совокупный трудовой потенциал всех работников предприятия равен L, часть которого может быть отдана коллективным, а остальное – частным хозяйствам. Пусть
![]() , (12)
, (12)
где
![]() .
Таким образом,
оставшаяся
доля L пойдет
на производство
в частных хозяйствах:
.
Таким образом,
оставшаяся
доля L пойдет
на производство
в частных хозяйствах:
![]() . (13)
. (13)
Отметим, что коэффициент варьируется именно частными хозяйствами, то есть они выбирают наиболее оптимальное распределение труда в зависимости от получаемой прибыли. Повышая плату за труд руководитель коллективного хозяйства влияет на выбор частными хозяйствами.
6.2.Производственные взаимосвязи.
Для дальнейших рассуждений введем производственную функцию. Валовой продукт агропромышленного предприятия в общепринятом понимании является функцией четырех параметров:
![]() . (14)
. (14)
Однако в данном случае будем рассматривать двухфакторную производственную функцию, так как, по предположению модели исследуемая взаимосвязь распространяется только на два параметра. Таким образом:
![]() . (15)
. (15)
Рассмотрим
производственную
функцию предприятий
коллективных
хозяйств (F2).
На производственное
потребление
расходуется
![]() ,
а труд, затраченный
на производство
выразится
формулой –
,
а труд, затраченный
на производство
выразится
формулой –
![]() .
Тогда производственная
функция примет
вид:
.
Тогда производственная
функция примет
вид:
![]() или исходя
из (9)
или исходя
из (9)
![]() . (16)
. (16)
Конечный продукт предприятия выразится следующим образом:
![]() , (17)
, (17)
то есть валовой продукт делится на производственное потребление предприятия как такового и поддержку частных хозяйств. Естественно предположить, что целью коллективных хозяйств будет увеличение объемов конечного продукта. Для этого разумно положить зависимость (9) линейной,
![]() . (18)
. (18)
причем
при нулевом
вложении труда
в коллективные
хозяйства
помощь частным
тоже должна
быть нулевая
и где
![]() .
О множестве
K следует
сказать отдельно.
Очевидно, что
оно имеет следующий
вид: K=[0, kmax].
Для определения
kmax
можно воспользоваться
моделью, рассмотренной
в предыдущей
главе. При анализе
случая, когда
часть валового
продукта идет
на инвестирование
производства,
а остальное
на поддержку
частных хозяйств
было получено,
что расширенное
воспроизводство
предприятия
будет иметь
место при следующем
соотношении
экономических
коэффициентов:
.
О множестве
K следует
сказать отдельно.
Очевидно, что
оно имеет следующий
вид: K=[0, kmax].
Для определения
kmax
можно воспользоваться
моделью, рассмотренной
в предыдущей
главе. При анализе
случая, когда
часть валового
продукта идет
на инвестирование
производства,
а остальное
на поддержку
частных хозяйств
было получено,
что расширенное
воспроизводство
предприятия
будет иметь
место при следующем
соотношении
экономических
коэффициентов:
![]() .
.
То
есть
часть производственного
потребления
должна обязательно
поступать в
коллективное
производство.
Таким образом,
максимальный
отток продукта
должен составить
![]() или
или
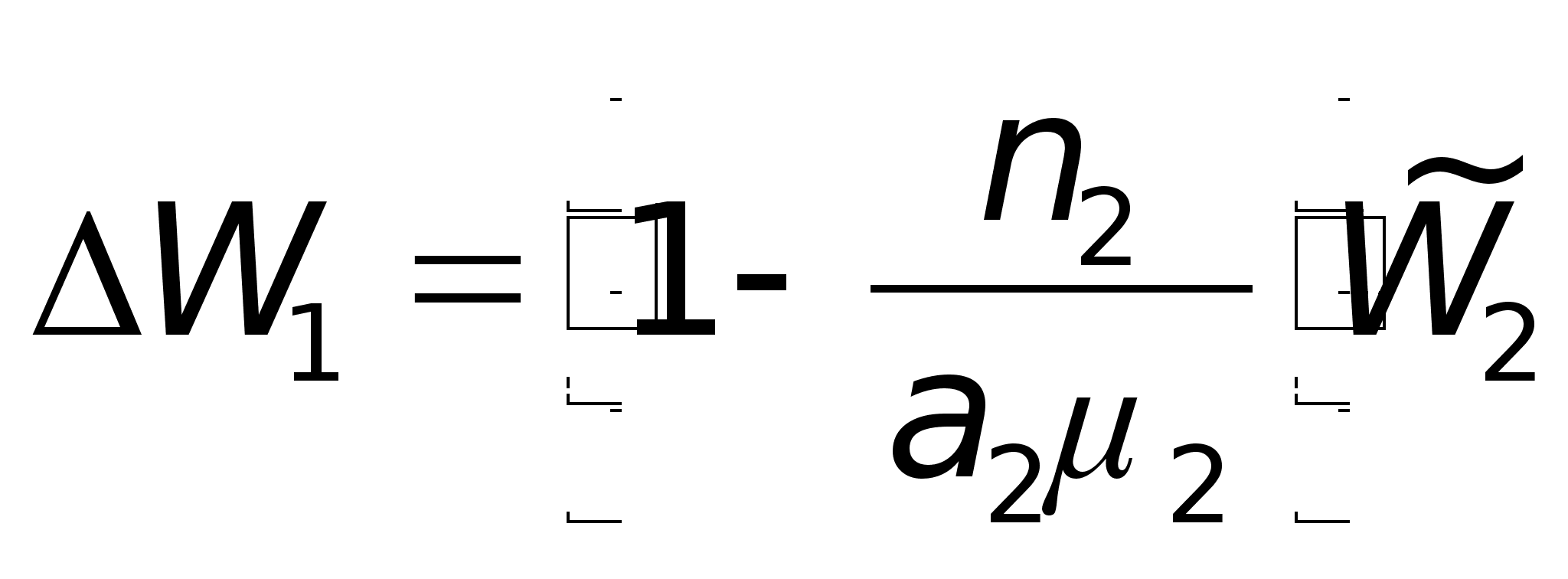 . (19)
. (19)
Тогда kmax может быть получено преобразованием выражения (18) с использованием (19):
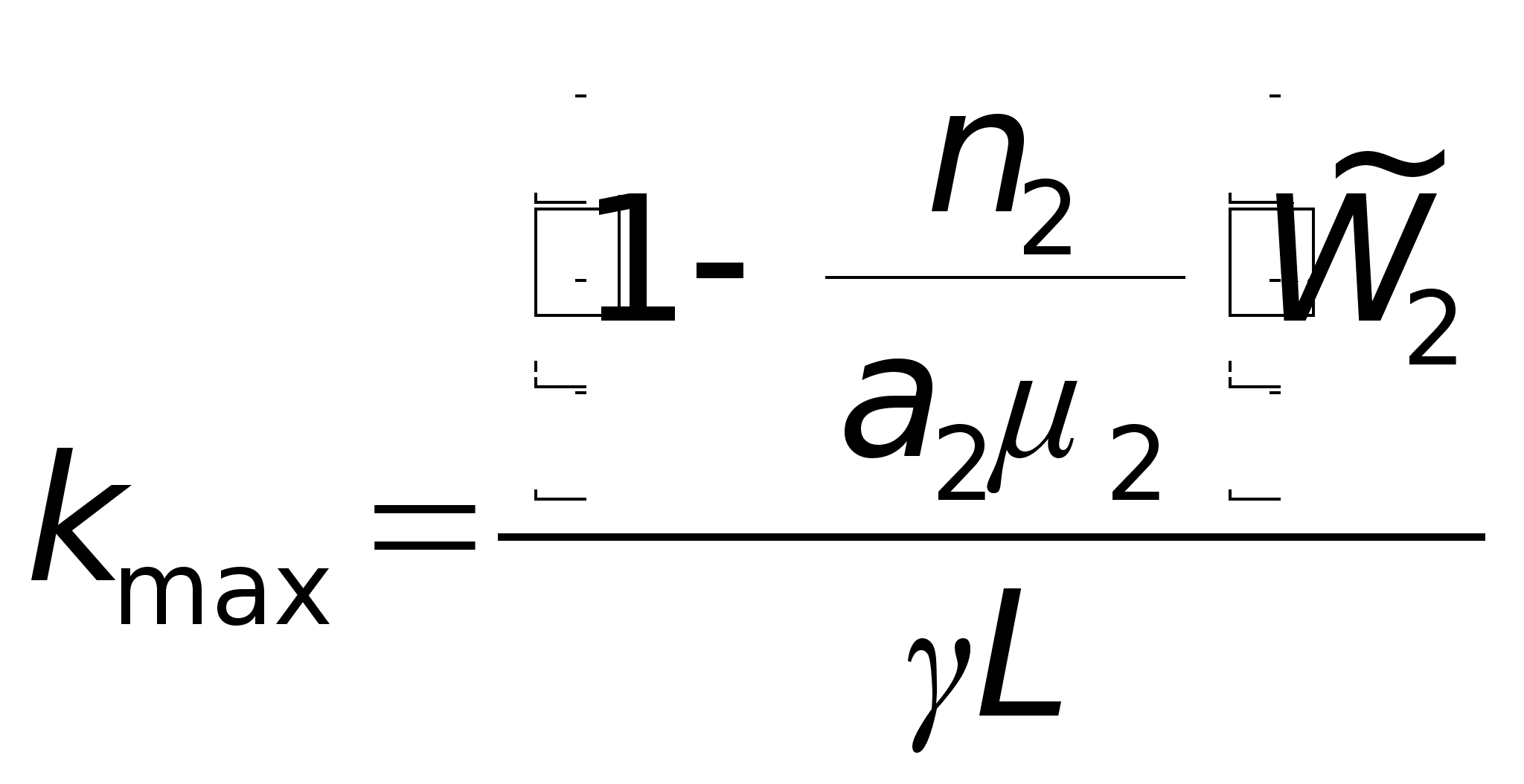 или
или
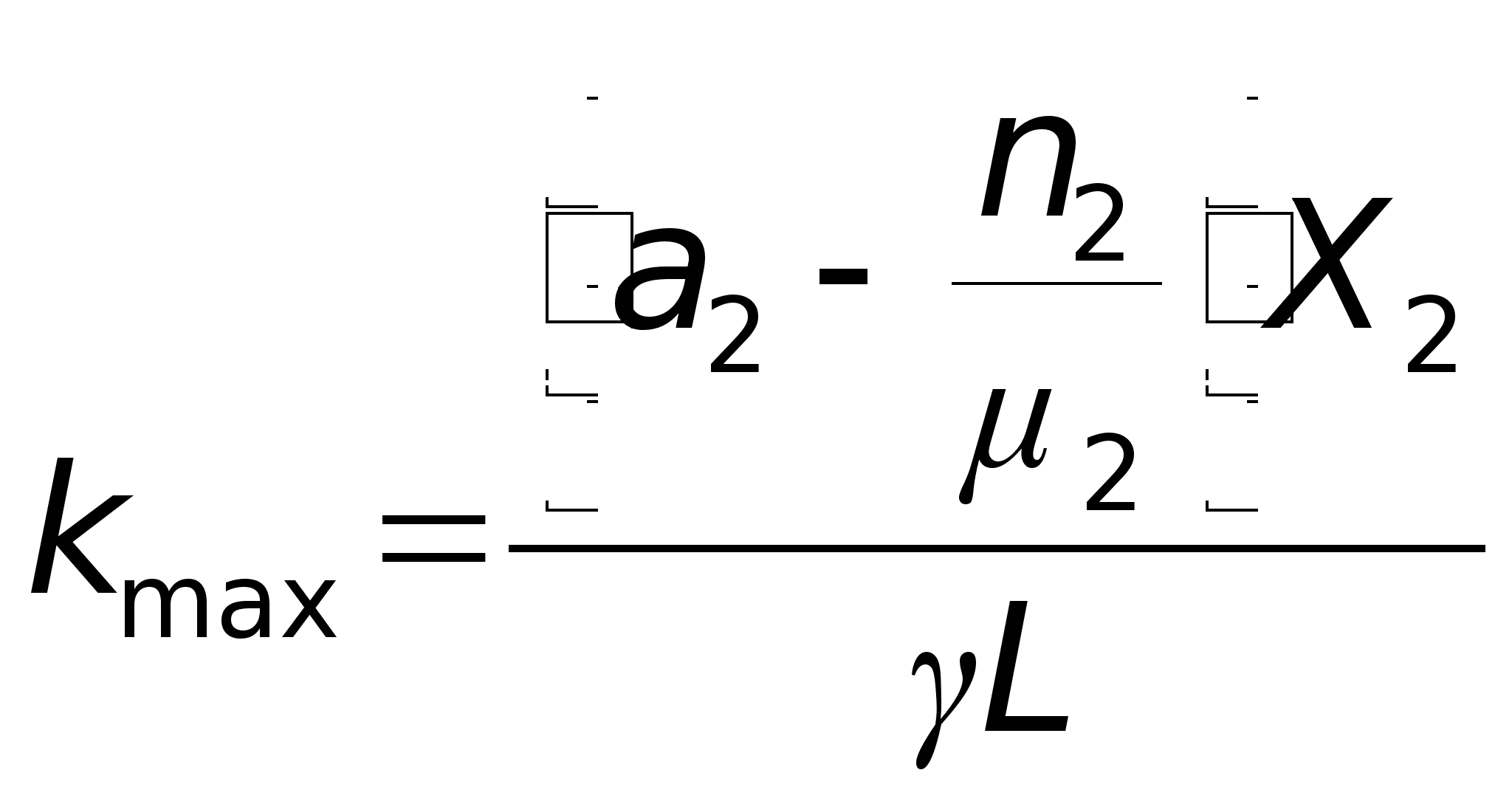 . (20)
. (20)
С другой стороны, можно действовать следующим образом. Предположим, что предприятие не получает никакой прибыли, однако оно должно покрыть амортизацию оборудования и заплатить зарплату своим работникам, для чего необходимо выполнение следующего неравенства:
![]() . (21)
. (21)
Где S – коэффициент оплаты труда. В этом случае в предприятии будет иметь место простое воспроизводство. Таким образом максимальный размер выделяемой помощи не должен превышать
![]() . (22)
. (22)
В результате получим:
![]() . (23)
. (23)
С учетом вышеприведенных рассуждений формула (17) перепишется следующим образом:
![]() . (24)
. (24)
Рассмотрим теперь, из каких компонентов складывается прибыль «частников». Очевидно, что это конечный продукт и заработная плата (инвестиции в данном случае принимаем равными нулю). Производственная функция будет следующей:
![]() , (25)
, (25)
при этом учтем, что производственное потребление будет удовлетворено в необходимом количестве, т. е. W1 не зависит от распределения труда. Тогда прибыль составит:
![]() . (26)
. (26)
При этом два последних слагаемых означают соответственно помощь от коллективных хозяйств и заработную плату, а S – это коэффициент оплаты труда.
Работники выбирают такое распределение трудовых ресурсов, при котором прибыль будет максимальной:
![]() . (27)
. (27)
В результате получаем следующую задачу оптимизации:
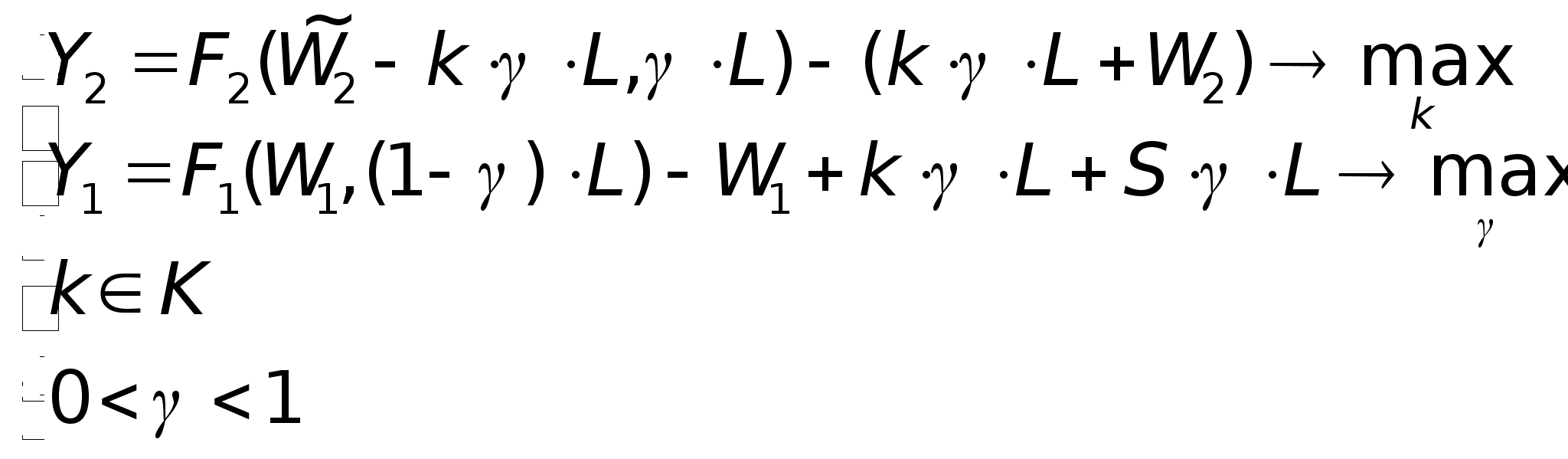 (28)
(28)
Рассмотрим
второе соотношение.
Для достижения
максимума
необходимо,
чтобы
![]() ,
и соответственно:
,
и соответственно:
![]() , (29)
, (29)
что доставляет максимум функции Y1. Подставляя (29) в (28), получим:
![]() . (30)
. (30)
Для
этого необходимо,
чтобы
![]() .
.
В результате решения этого уравнения находится k=k*, оптимальное с точки зрения максимума функции Y2. Параметр =* вычисляется по формуле (29). Полученное решение (k*,*) отражает состояние равновесия между подсистемами.
Также представляет интерес трансформация задачи (28) в следующий вид:
![]() . (31)
. (31)
Смысл этого выражения заключается в том, что руководитель предприятия является, как бы более "ответственным" за состояние сельского хозяйства в целом и преследует целью увеличение прибылей как коллективного, так и частных хозяйств. Коэффициент показывает степень "важности" того или иного критерия и удовлетворяет условию 0
6.3.Взаимодействие сельхозпредприятий и личных хозяйств для частного случая производственной функции.
Как
уже было упомянуто
выше, с помощью
максимизации
выражения (27)
необходимо
найти зависимость
![]() и на основании
этого вычислить
оптимальное
значение k*.
и на основании
этого вычислить
оптимальное
значение k*.
Для этого предположим, что производственная функция предприятий имеет вид функции Кобба-Дугласа:
![]() , (32)
, (32)
где
A = const > 0 – некоторый
коэффициент,
а
![]() .
.
Тогда валовой продукт частных хозяйств выражается следующим образом:
![]() . (33)
. (33)
Отсюда формула (27) примет следующий вид:
![]() . (34)
. (34)
Подсчитаем производную полученной функции. Она равна
![]() . (35)
. (35)
Для достижения максимума прибыли необходимо, чтобы
![]() .
.
Таким образом
![]() . (36)
. (36)
Рассмотрим
поподробнее
вид полученной
зависимости.
При возрастании
k увеличивается
"поощрение"
трудового
вклада работника
в коллективное
хозяйство путем
увеличения
поддержки при
одном и том же
вкладе. Таким
образом, члену
кооператива
становится
выгоднее распределить
свой трудовой
потенциал в
пользу кооператива.
Следовательно,
функция (k)
монотонно
возрастает
на
![]() или
или
![]() .
Однако величина
.
Однако величина
![]() убывает с
возрастанием
k так как
при распределении
своего труда
в пользу кооператива
работнику
остается меньше
времени для
производства
собственной
продукции. В
результате
ситуация стремится
к моменту когда
член кооператива
не сможет найти
время на то
чтобы воспользоваться
выделенной
ему поддержкой.
Отсюда можно
сделать вывод,
что функция
(k)
вогнута. Таким
образом, отметим
следующие
свойства зависимости
=(k):
убывает с
возрастанием
k так как
при распределении
своего труда
в пользу кооператива
работнику
остается меньше
времени для
производства
собственной
продукции. В
результате
ситуация стремится
к моменту когда
член кооператива
не сможет найти
время на то
чтобы воспользоваться
выделенной
ему поддержкой.
Отсюда можно
сделать вывод,
что функция
(k)
вогнута. Таким
образом, отметим
следующие
свойства зависимости
=(k):
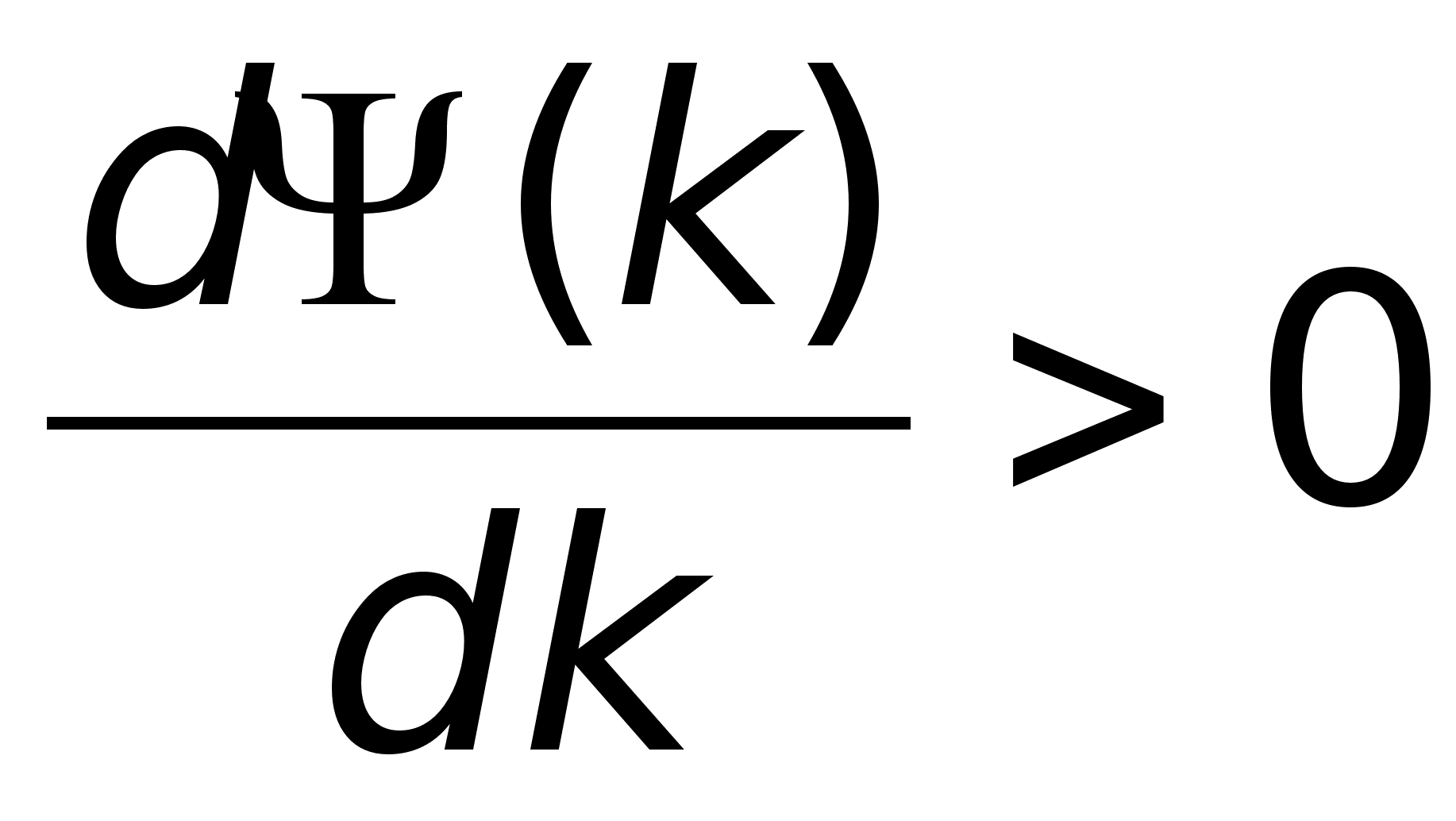 ,
для
,
для
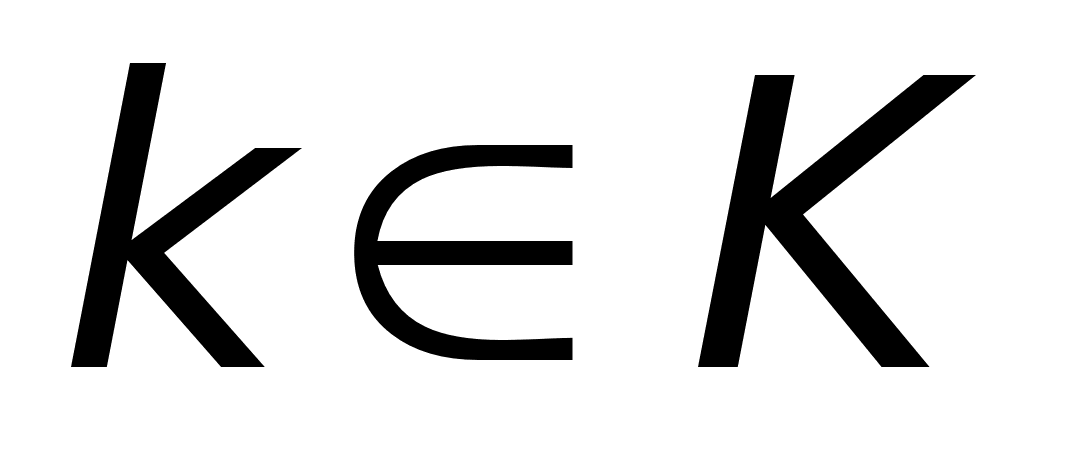 .
.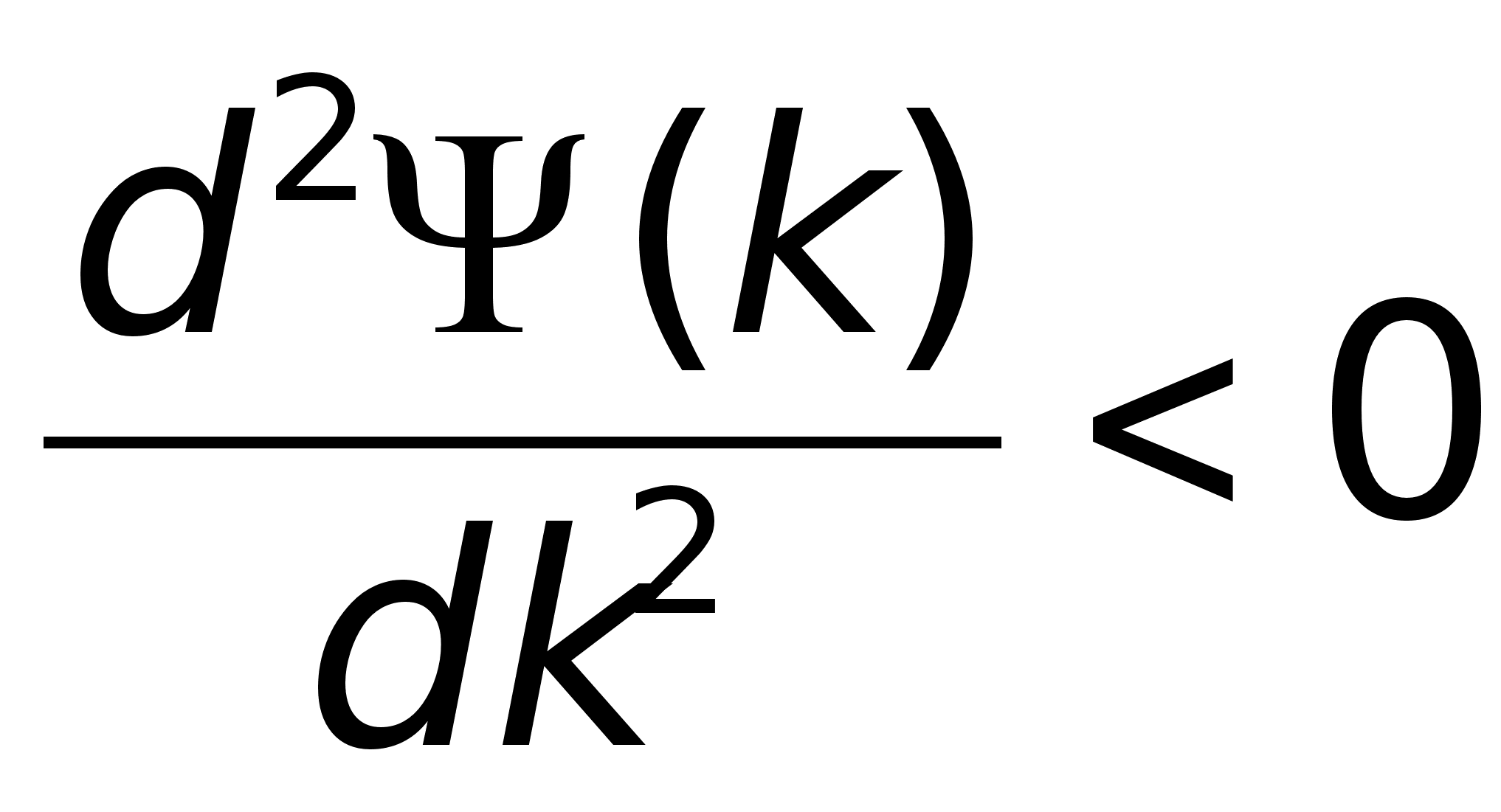 ,
для
,
для
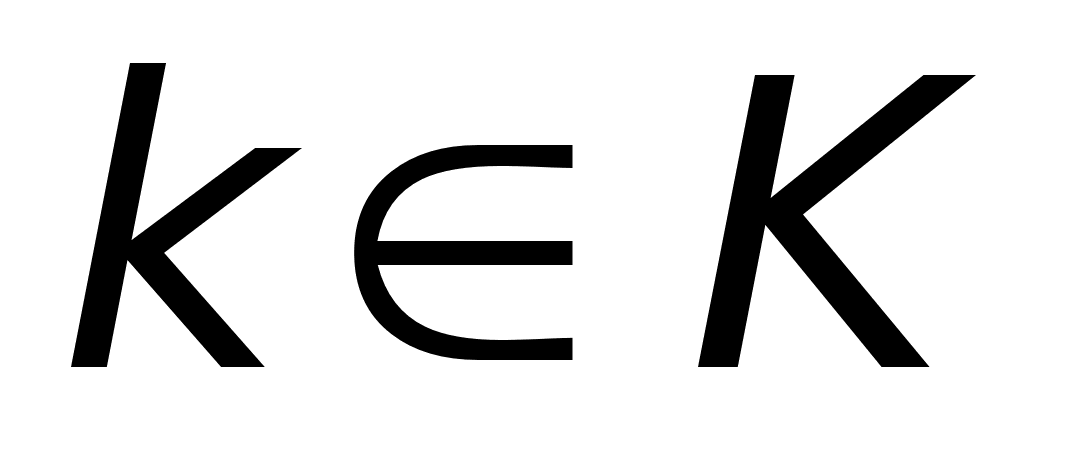 .
.
График
этой функции
для
![]() ,
,
![]() ,
,
![]() ,
,
![]() представлен
на рис. 6.3.1.
представлен
на рис. 6.3.1.
р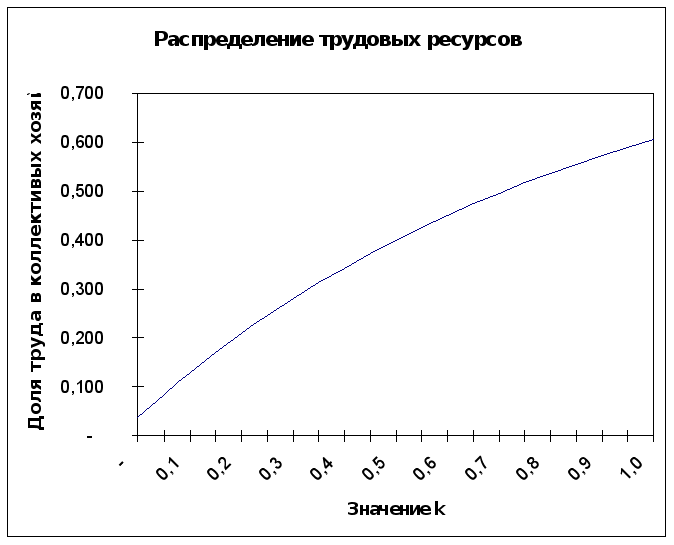
ис.
6.3.1.
Видно, что построенный график удовлетворяет вышеперечисленным условиям.
Производственная функция сельхозкооператива имеет вид:
![]() . (37)
. (37)
Конечный продукт получается путем вычитания производственного потребления и поддержки частников из валового продукта:
![]() . (38)
. (38)
Подставляя в это соотношение вместо рассмотренную выше функцию =(k) получим:
![]() . (39)
. (39)
На
рис. 6.3.2 изображен
график этой
функции. Видно,
что она имеет
максимум на
![]() .
Именно для
значения k*
достигается
максимальная
прибыль предприятия
АПК.
.
Именно для
значения k*
достигается
максимальная
прибыль предприятия
АПК.
Р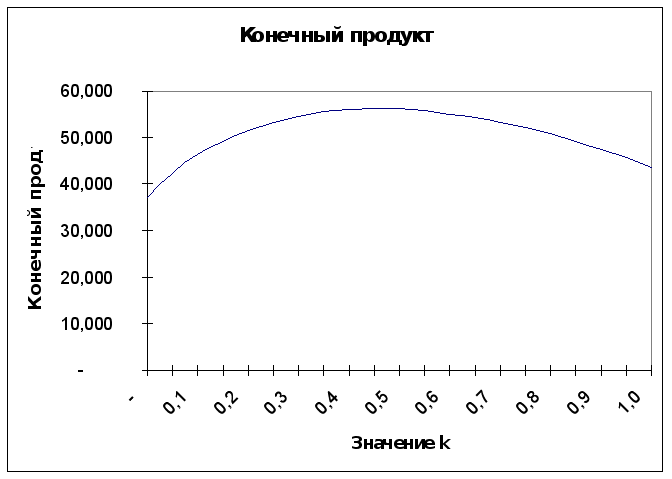
ис.
6.3.2
К сожалению, аналитически выразить k* не представляется возможным, однако, используя численные методы, его можно найти. В данном случае оно равно примерно 0,63. Таким образом, администрация коллективного хозяйства должна выбрать соответствующий коэффициент поощрения k, основываясь на показателях своего производства и на отличительных его особенностях.
Вернемся к задаче (31). Напомню, что она характеризует действия дирекции, направленные не просто на увеличение прибыли своего хозяйства, но и на увеличении прибыли частных хозяйств. В данном случае вместо в функции Y1 и Y2 нужно подставить =(k). Задача примет следующий вид:
![]() . (40)
. (40)
Данная проблема также представляет интерес и должна быть рассмотрена руководством предприятия.
В заключение отметим, что вид графиков, представленных на рис. 6.3.1 и 6.3.2 может меняться от показателей производства, таких как фондоотдача, производительность труда и т. д. Максимум k может быть достигнут и не границе множества K.
7.Заключение.
В работе рассмотрена структура системы производства сельхозпродукции, сложившаяся в настоящее время в районных АПК Тверской области. Из результатов рассмотрения следуют выводы.
Из анализа статистичестких данных функционирования районных АПК, можно утверждать, что основными производителями сельхозпродукции в России сейчас являются сельхозпредприятия с различными формами собственности и частные хозяйства работников этих предприятий. Причем наблюдается взаимная интеграция этих производств, связанная с оттоком финансовых средств из первых во вторые. При дальнейшем сохранении сложившегося взаимодействия, существует угроза полного развала этого сектора экономики и экономики страны в целом.
Проведен анализ функционирования и взаимодействия подсистем частных и коллективных хозяйств. Разработана математическая модель, позволяющая для определенных условий находить оптимальное решение задачи, при котором сельхозкооперативы оптимизируют прибыль не препятствуя функционированию личных хозяйств. Для этого предложена схема, на основе которой предоставление материальных ресурсов (помощи) частным хозяйствам зависит от труда, вложенного в производство сельхозпредприятий. Основная идея состоит в том, что при определенном характере (количественном значении) помощи личным хозяйствам со стороны сельхозпредприятий, работникам оказывается выгодным выделять для работы на предприятиях необходимую для последних часть своего труда.
Для конкретного примера произведены расчеты по оптимизации конечного продукта и проанализирован вид полученных зависимостей.
Основная идея решения состояла в том, чтобы ввести в зависимость выделение помощи от количества труда, вложенного в кооператив. Исходя из этого, предположительно можно добиться того, чтобы членам кооператива было выгоднее в нем работать, что решит проблему в целом.
8.Литература
Каданер Э.Д. Динамическое моделирование экономических систем. Пермь, 1990.
Ждакаев С. Конец диктатуры ленивых. // Известия, 17.02.98.
Лисичкин Г. Бывшие «братья» в поисках выхода из аграрного тупика. // Известия, 10.08.97.
Пугачев В.Ф., Пителин А.К. Анализ вариантов антиинфляционной экономической политики экономике // Экономика и математические методы, 1996’1.
Пугачев В.Ф., Пителин А.К. Инфляция в технически отсталой монополизированной экономике // Экономика и математические методы, 1995’1.
Основы теории оптимального управления. Под ред. Кротова. Москва, 1990.
Моисеев Н. Н. Математические задачи системного анализа. Москва «Наука», 1981.
Хромов Ю.С. Производственная безопасность России: внутренние и международные аспекты // Общество и экономика, 1994’9-10.
Дроздов Н.Д. Введение в прикладное математическое моделирование. Методология и логика прикладной математики. Тверь, ТвГУ, 1994.
Статистические данные хозяйствования Максатихинского и Конаков ского районов в 1992-96 гг.
Вахина Н.Д. “Анализ состояния и перспектив развития Максатихинского района”. Дипломная работа. Научный руководитель Дроздов Н.Д., Тверское заочное отделение Северо-западной академии государственной службы. Тверь 1997 г.
Рассказова В.Н. “Анализ состояния и перспектив развития Конаковского района”. Дипломная работа. Научный руководитель Дроздов Н.Д., Тверское заочное отделение Северо-западной академии государственной службы. Тверь 1997 г.
36
