Реферат: Расчет надежности, готовности и ремонтопригодности технических средств и вычислительных комплексов

Республика Армения г.Ереван,

Российско-Армянский Государственый университет

Расчет надежности, готовности и ремонтопригодности технических средств и вычислительных комплексов

2002г.

Курсовой проект

Спец. Курс:

“Технологии тестирования, диагностирования

и отладки технических средств и программ-

ного обеспечения вычислительных комплек-

сов.”

Факультет:Прикладной математики и информатики.

Кафедра:Системного програмирования.

Специальность:Системный программист.

Студентка:III курс Асланян Асмик

Руководитель:ст. Преподаватель РАУ к.т.н.Нахапетян С.Х.

1.Введение

Вычислительной системой (ВС) будем называть совокупность вычислительных средств, включающих не менее двух вычислительных машин или процессов предназначенных для автоматической обработки информации в соответствии с заданным алгоритмом.

Качеством называется совокупность свойств, определяющих пригодность использования вычислительной машины или системы , по назначению. Качеством является совокупностью свойств, поэтому оно оценивается множеством показателей. Выбор показателей определяется назначением вычислительной машины или системы, ее структурой, видом избыточности, длительностью функционирования и т.п. Показатель качества - это вектор, компонентами которого служат показатели свойств, являющиеся частными показателями качества.

Показатели качества можно классифицировать по пригодности, оптимальности и превосходству. Вычислительные машины или системы, удовлетворяюие показателям оптимальности- являются наилучшими , т.е. обладают наивысшим качеством; удовлетворяющие показателям превосходства считаются превосходящими по качеству остальные машины или системы.

При оценке качества вычислительной системы в процессе ее разработки или эксплуатации встречаются с двумя трудностями. В большинстве случаев не удается установить единый обобщенный показатель качества, который позволил бы сравнить пазличные системы и выбрать наилучшую. Это объясняется тем, что качество оценивается множеством свойств.

Вторая трудность состоит в том, что не существует методики установления требований на показатели качества. Это объясняет тем, что не удается разработать на все случаи жизни критерия оптимальности системы в смысле ее качества.

Основными характеристиками вычислительных машин и систем, определяющими их качество, являются надежность, ремностопригодность, готовность , эффективность.

Надежностью называется свойство технического устройства сохранять свои характеристики в данных условиях эксплуатации.

Показателями надежности невосстанавливаемых вычислительных машин и систем могут быть: вероятность безотказной работы , среднее время безотказной работы T, частота отказов , и интенсивность отказов .

Показателями надежности восстанавлимаемых машин и систем являются : средняя частота отказов и наработка на отказ .

Показатели надежности связаны, между собой зависимостями:

(1.1)

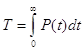
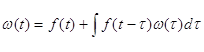
Показатели надежности невосстанаялияаемых систем могут также характеризовать надежность восстанавливаемых систем, если оценивается их функционирование до первого отказа. При этом восстановление отказавших резервных устройств допускается в прецессе работы машины или системы.

Наличие больших чисел показателей вовсе не означает, что всегда необходимо оценивать надежность вычислительной системы по всем показателям.

Наиболее полно характеризует надежность невосстанаялияаемой системы частота отказов. Это объясняется тем, что является плотностью распределения, а поэтому несет в себе всю информацию о случайном явлении-времени безотказной работы.Такие характеристики, как вероятность безотказной работы, интенсивность отказов, среднее время безотказной работы являются лишь характеристиками распределения и всегда могут быть получены, если известно . Однако оценивать надежность вычислительной системы частотой отказов в большинстве случаев нецелесообразно, так как она не обладает достаточной наглядностью и не входит в другие более общие характеристики качества ВС. Она используется обычно при определении доверительных вероятностей при обработке данных статистичесих испытаний технических устройств.

Интенсивность и средняя частота отказов – наиболее удобныe характеристики надежности простых элементов. Это объясняется тем, что интенсивности отказов многих экементов электроники и вычислительной техники есть величины постоянные и характеризуются одним числом. Кроме того, по этим характеристики надежности машины и системы.

Среднее время безотказной работы является достаточно наглядной характеристикой надежности невосстанавливаемых машин и ВС. Однако применеие этого показателя нецелесообразно в тех случаях, когда время работы ВС гораздо меньше среднего времени безотказной работы, закон распределения времени безотказной работы, закон распределения времени безотказной работы не однопараметрический и для достаточно полной оценки требуется моменты высших порядков, машина или ВС резервированы, интенсивность отказов непостоянна, элементы ВС работают не одновременно.

Ремонтопригодностью называется способность технического устройства к восстановлению в процессе эксплуатации. Показателями ремонтопригодности могут быть: вероятность восстановления системы за заданное время , среднее время восстановления , закон распеределения времени восстановления , интеносивность восстановления .

Вероятность является интервальным показателем , - интегральным, а и -точечными показателями ремонтопригодности.

Наиболее часто для оценки ремонтопригодности ВС применяется среднее время восстанавления. Эта характеристика наиболее наглядна, она во многом определяет такой важный показатель качества ВС, как готовность. Она является интегральной, поэтому обладает следующим недостатком: неполно характеризует ремонтопригодность ВС, если закон распределения времени восстаналения не однопараметричный и для оценки ремонтопригодности требуется знание моментов высшего порядка.

Важнейшей характеристикой ремонтопригодности технических устройств вычислительных машин и систем является интенсивность их восстановления. Это объясняется тем, что большинство показателей качества ВС в процессеих проектирования вычисляются через интенсивности восстановления их устройств.

Готовностью называется способность технического устройства быть готовы м к действию в любой момент времени. Она зависит от надежности и от ремонтопригодности ВС.Чем выше надежность и ремонтопригодность ,тем выше готовность.Показателями готовности могут быть: функция готовности и коэффициент готовности .

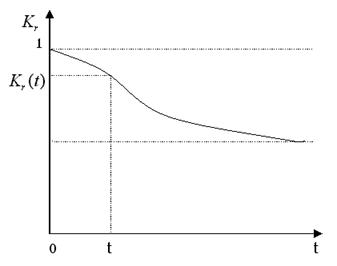
Функция готовности есть вероятность того, что в любой момент времени система готова к действию. Эта характеристика обычно имеет вид, показанный на рис. 1.1. Из рисунка видно, что =1, т.е. считается, что ВС начинает эксплуатироваться исправной. С ростом убывает и при функция готовности стремится к постоянной, отличной от нуля величине, которая является финальной вероятностью и называется коэффициентом готовности. Таким образом, между функцией и коэффициентом готовности существует зависимость . (1.2)

Функция и коэффициент готовности являются характеристиками точечными. Эта означает, что ордината , показанная на рис. 1.1, есть вероятность того, что в момент времени система исправна. До момента она могла сколь угодно раз отказывать и ремонтироваться.

Коэффициент готовности легко вычисляется, если известны интегральные характеристики надежности и ремонтопригодности

(1.3)

где -наработка на отказ вычислительной системы; - среднее время восстановления ВС.

Функция готвности может иметь возрастающей функции или колебательной. В случае возрастающей функции, когда в начале эксплуатации Вс имеет неисправные резервные устройства .

Если же анализ готовности системы начинается с момента времени, когда система вообще неисправна и ремотируется, то .

Колебательный процесс изменения функции готовности наблюдается при обслуживании ВС с определенным видом приоритета и длительностью времени восстановления.

Независимо от вида кривых финальная вероятность для данной системы всегда постоянна и имеет одно и то же значение, определяемое выражением (1.3), т.е. коэффициент готовности не зависит от начального состояния ВС, из которого начинается ее эксплуатация.

2. Надежность, готовность и ремонтопригодность технических средств и вычислительных комплексов

2.1 Граф состояний вычислительной системы

Вычислительная система в процессе функционирования может находиться в большом числе различных состояний. Например, все устройства системы исправны или i-е (i=1,2,…,N) устройств отказало, а остальные исправны, или i-е и j-е устройства отказали, а остальные исправны и т.п. При восстановлении отказавших устройств система в дискретные моменты времени переходит из одного состояния в другое. В процессе длительной экслпуатации она может побывать в каждом из возможных состояний многократно. Тогда ее функционирование может быть описано графов, узлы которого соответствуют состояниям системы, а ветви указывают все возможные переходы из состояния.Если в графе имеется n узлов, то среди них будет k узлов, отражающих отказовые состояния, и n-k узлов, отражающих исправные состояния.

Часто интересуются функционированием системы до некоторого l–го состояния , например до первого ее отказа. Тогда l-е состояние называется поглощающим. Система, попавшая в l-е состояние, уже не может перейти в другие, и в графе отсутствуют ветви переходов из этого состояния (экран).

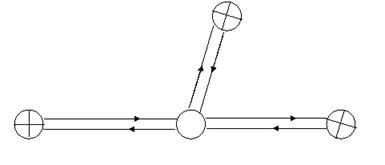
Вид графа зависит от структуры системы (схемы расчета надежности), числа обслуживающих бригад и дисциплины обслуживания. Обычно узлы графа нумеруются и отмечаются (например, крестом) те, которые соответствуют отказвым состояниям системы. На графе также указываются все интенсивности переходов.

N 2

Рис.2.1 Граф состояний восстанавливаемой нерезервированной машины

Сформулируем ряд важных свойств графов состояний:

1.Граф состояний полностью описывает функционирование ВС как системы массового обслуживание. Вид графа определяется структурной схемой системы, надежностью и ремнотопригодностью элементов, а также дисциплиной обслуживания системы. На основании этого свойства можно утверждать, что все количественные характеристики надежности, готовности и ремонтопригодности ВС могут быть определены непосредственно из графа ее состояний.

2.Граф, не содержащий поглощающих состояний, описывает поведение системы при неограниченном ремонте.

3.Число узлов графа состояний может быть больше или меньше 2n где n - число элементов структурной схемы. Это объясняется тем, что граф описывает поведение ВС совместно с обслуживающим органом.

4.Функционирование ВС при обратном приоритете обслуживания отказавших элементов описывается графом типа дерева.

2.2 Описание функционирования вычислительной системы дифференциальными уравнениями

Составить систему дифференциальных уравнений для определения количественных характеристик надежности, готовности и ремонтопригодности ВС можно по виду графа состояний системы. Сформулируем первоначально правило состовления уравнений для определения вероятности пребывания системы в i-м состоянии в момент времени t. Часть графа с состотянием i-1,i,i+1 показана на рис.2.2 Тогда дифференциальное уравнение для вероятности пребывания системы в i-м состоянии в момент времени t будет иметь вид:

Из уравнения видно, что слева пишется производная по времени от вероятности пребывания системы, в i-м состоянии в момент времени t, а справа – сумма произведений интенсивностей переходов из всех соседних состояний в i-е состояние и из i-го – во все соседние на соответствующие вероятности состояний. Знаки в правой части уравнения определяются по направлению стрелок в ветвях графа. Если стрелка направлена в i-е состояние, то при соответсвующей ей интенсивности перехода ставится знак “+”, в противном случае – знак “-”. Это правило справедливо при любом числе соседних с i-м состояний.

Рис.2.2 Фрагмент графа состояний системы

2.3 Анализ надежности, ремотопригодности и восстанавливаемости ВС по уравнениям функционирования

Рассмотрим способы определения количественных характеристик надежности ВС при следующих допущениях:

– поток отказов элементов системы являются простейшими,

– время восстановления изменяется по показательному закону,

– котроль состояния системы непрерывный,

– обслуживание осуществляется при неограниченном восстановлении.

При указанных предположениях будем определять следующие количественные характеристики надежности, готовности и ремонтопригодности системы: вероятность безотказной работы, среднее время безотказной работы, функцию и коэффициент готовности, наработку на отказ и среднее время восстановления системы.

Для определения вероятности безотказной работы строится граф состояний системы. На графе отмечаются все отказовые состояния, из которых запрещаются переходы в соседние исправные состояния (ставятся экраны). По графу состояний формально записывается система дифференциальных уравнений. Из анализа модели функционирования системы формулируются начальные условия эксплуатации. При определении вероятности безотказной работы в течение времени t обычно предполагается, что в момент t=0 все элементы системы исправны, т.е. эксплуатация начинается с нулевого состояния (нулевого уровня). Тогда начальными условиями функционирования системы будут , . При этих начальных условиях можно определить вероятность безотказной работы в течение времени t, используя одно из следующих соотношений:

(2.1)

(2.2)

где N+1 - число узлов в графе, равное числу состояний системы; k- число узлов графа, соответствующих исправным состояниям системы; - вероятность того, что система я течение времени t попадет в i-е исправное состояние; - вероятность того, что система я течение времени t попадет в j- е отказовое состояние.

Если число исправных состояний системы больше, чем отказовых, то следует пользоваться соотношением (2.1), в противном случае целесообразно использовать (2.2).

Вероятность и при известных начальных условниях всегда можно определить из исходной системы дифференциальных уравнений. Наиболее просто найти искомые вероятности в преобразованиях Лапласа с последующим отысканием оригиналом функций и .

Среднее время безотказной работы может быть вычисленно при известной вероятности безотказной работы по формуле . Так как по определению 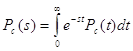, то при s=0 имеем

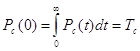. (2.3)

Из этого выражения видно, что для определения среднего времени безотказнох работы достаточно найти преобразование Лапласа вероятности безотказной работы системы и в полученное выражение подставить s=0.

Для определения функции готовности строится граф состояний системы, на графе отмечаются все отказовые состояния и составляется формально по виду графа система дифференциальных уравнений. Для определения используется одно из следующих соотношений:

(2.4)

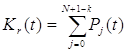(2.5)

где - вероятность застать систему в момент времени t в i-м испраном состоянии; - вероятность застать систему в момент времени t в j-м неисправном состоянии; k-число узлов графа, соответствующих исправным состояниям системы; N+1 –общее число узлов в графе, равное числу состояний системы.

Если число отказовых состояний системы меньше числа исправных, то следует пользоватся выражением (2.5), в противном случае (2.4).

Вероятности и вычисляются так же, как и в случае определения вероятности безотказной работы.

Сравнивая процедуры вычисления вероятности безотказной работы и функции готовности, можно убедиться, что они идентичны. Отличие состоит лишь в том, что при определении функции готовности, можно убедиться, что они идентичны. Отличие состоит лишь в том, что при опрделении функции готовности в графе состояний системы отсутствуют поглощающие состояния, а поэтому в системе дифференциальных уравнений появляются дополнительные члены.

Коэффициент готовности является финальной вероятностью пребывания системы в исправном состоянии. Его легко вычислить, если известна функция готовности или , воспользовавшись соотношением

(2.6)

Из этого соотношения видно, что для определения коэффициента готовности достаточно из уравнений функционирования системы найти преобразование Лапласа коэффициента готовности и вычислить предел. Функция готовности системы при неограниченном востановлении обычно имеет вид:

(2.7)

причем .

Тогда для вычисления предела достаточно в функции , определяемую выражением (2.7), подставить s=0. Из (2.6) и (2.7) следует:

(2.8)

Так как , то

(2.9)

Это соотношение может быть весьма полезным при определении наработки на отказ или среднего времени восстановления системы.Для получения одного из этих показателей нет необходимости решать систему уравнений типа массового обслуживания. Достаточно лишь вычислить свободные члены и в выражении (2.7). В дальнейшем будет показано, что и модут быть получены непосредственно из графа состояний системы.

Коэффициент готовности, ялвляясь финальной вероятностью, не зависит от выбора начальных условий. Начальные условия определяют лишь переходные процессы в системе массового обслуживания типа система-ремонтоное предприятие. Это следует иметь в виду при составлении и решении уравнений функционирования системы. Вычислять коэффициент готовности целесообразно при таких начальных условиях, при которых достигается наибольшая простота раскрытия определителей.

Решение большого количества прикладных задач показывает , что переходные процессы в системах массового обслуживания, применительно к задачам надежности вычислительных систем обшего назначения, практически заканчиваются уже после двух-трех восстановлений. Поэтому часто на практике не интересуются функцией готовности, а за основу количественную характеристик надежности принимают коэффициент готовности.

Наработка на отказ является математическим ожиданием времени между соседними отказами восстанавливаемой системы. Эта характеристика мажет быть вычислена из соотношения:

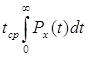(2.10)

где - вероятность того, что в течение времени t, отсчитанного от момента начала работы системы после i-го ее восстановления, не возникает отказ всей системы, т.е. , где - время между началом работы устройства после i-ого восстановления и (i+1)-м отказом. Вероятность может быть определена из системы уравнений функционирования системы.

Для определения наработки на отказ нет необходимости вычислять и интегрировать в соответствии с выражением (2.10). Достаточно найти преобразование Лапласа вероятности . Так как по определению

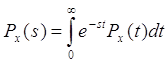, то

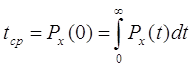(2.11)

Из последнего выражения видно, что для получения наработки на отказ достаточно найти, как и в случае вычисления среднего времени безотказной работы, преобразование Лапласа суммы вероятностей исправных состояний системы и положить в полученном выражении s=0, Отличие состоит лишь в том, что вероятность определяется при начальных условиях, отличных от начальных уловий , при которых определяется вероятность в выражении (2.3).

Описанный выше способ определения наработки на отказ применим лишь для частного случая, когда система имеет лишь одно отказовое состояние. В большинстве же практических случаев таких состояний много. Так же практических случаев таких состояний много. Так например при эксплуатации нерезервированной системы , состоянщей из N элементов, можно получить N отказовых состояний (Рис.2.1). В таких случаях определлить из уравнений функционирования системы затруднительно. Это объясняется тем, что неизвестно, при каких начальных условиях следует определять , так как предотказовых состояний может быть несколько, так как предотказовых состояний может быть несколько.

В ряде случаев удается найти наработку на отказ, воспользовавшись общей формулой для коэффициента готовности

(2.12)

Пользоваться этой формулой на практике целесообразно в следующих случаях:

среднее время восстановления системы известно из опыта;
система имеет лишь одно отказовое состояние, причем из этого состояния в соседние возможен переход с одной и той же интенсивностью 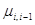. Тогда ;
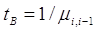система имеет несколько отказовых состояний, но интенсивности переходов из этих состояний в соседние одинаковы. Тогда среднее время восстановления системы равно, как в прежнем случае, .

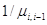Случаи 2 и 3 легко распознаются по графу состояний. Тогда для определения наработки на отказ достаточно найти описанным ранее способом.

На практике наиболее часто встречаются случаи, когда число отказовых состояний, системы велико, а значения интенсивностей восстановления зависят от отказового состояния. Тогда среднее время восстановления системы неизвестно, а наработку на отказ невозможно определить непосредственно по формуле (2.12).

Покажем, что среднее время восстановления и наработку на отказ мажно определить, если известны финальные вероятности пребывания системы во всех возможных состояниях и интенсивности переходов из отказовых в предотказвые состояния.

Интенсивность восстановления системы равна сумме произведений интенсивностей переходов из отказовых состояний в исправные на соответствующие вероятности отказвых состояний, т.е.

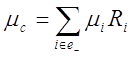(2.13)

где - вероятность того, что если система откажет, то она попадет в i-е отказовое состояние; - сумма интенсивностей переходов из i-го откаового состояния во все исправные состояния, граничащие с i-м отказовым состоянием; - подмоножество отказовых состояний, граничащих с исправными.

Вероятность легко вычислить по формуле

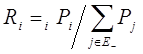(2.14)

где -финальная вероятность пребывания системы в i-м отказовом состоянии, граничащем с исправным; - финальная вероятность пребывания в j-м отказовом состоянии, граничащем или не граничащем с исправным состоянием; -подмножество всех отказовых состояний.

Интенсивности легко определить по графу состояний, воспользовавшись соотношением:

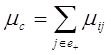(2.15)

где – интенсивность переходов из i–го отказового состояния в j–е граничащее исправное состояние; - подмножество исправных состояний, граничащих с отказовыми.

Подставляя занчения и из (2.14) и (2.15) в (2.13), получим:

(2.16)

Так как среднее время и интенсивность восстановления связаны соотношением 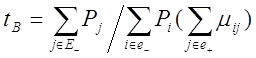(2.17)

Зная среднее время восстанояления, легко найти наработку на отказ, воспользовавшись зависимостью (2.12). Так как

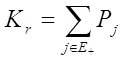, а ,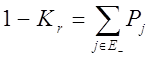

где Et - подмножество всех исправных состояний, то

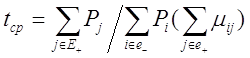. (2.18)

Заключение

Методы расчета, основанные на решении уравнений массового обслуживания, являются классическими. Однако они лишь в редких случаях могут буть использованы при оценке надежности, готовности и ремонтопригодности вычислительных систем. Это объясняется тем, что ВС являются резервированными, имеют сложную структуру и дисциплину обслуживания. Граф состояний таких систем имеет сотни и тысячи узлов. Большое число дифференциальных уравнений не дает возможности вычислить количественные характеристики даже с помошью ЦВМ.